随着同化观测资料种类和数据量的增多，以及同化技术和数值模式本身的发展和完善，数值天气预报准确率越来越高，但由于大气的混沌性，数值模式仍不可避免地存在随机误差（叶笃正等，2006；穆穆等，2011；杜钧和康志明，2014），且各种数值模式在分辨率、初始场、积分步长、物理参数化方案和动力框架等方面的不同导致模式预报误差也不尽相同。预报员面对多个模式的预报产品，仅凭借主观分析快速而准确地制作定量预报比较困难，尤其是模式降水预报具有离散性、非线性、非高斯特征，客观订正具有更大挑战。科学合理地进行多模式降水预报的本地化客观释用是提高降水预报水平的有效手段之一（任宏利和丑纪范，2007；毕宝贵等，2016）。

常用的定量降水客观订正方法，主要有针对单个模式进行系统性偏差订正的频率匹配法、最优评分订正法、百分位映射法等（Panofsky and Brier， 1968；Ebert， 2001；李俊等， 2014；智协飞和吕游， 2019；曹萍萍等，2023）。其中，频率匹配法通过统计实况与降水预报不同量级对应的频率，将有偏差的降水预报频率调整到对应量级的实况频率上（李莉等，2011；李俊等，2015；周迪等，2015）；最优评分订正法基于训练期模式降水量预报调整后的TS（Threat Score）评分最优化进行建模，以确定预报日降水分级订正系数（吴启树等，2017）；百分位映射法将模式预报转化为基于预报结果分布的百分位值，考虑模式与观测之间概率密度分布的偏差并对其进行订正（童尧等，2017）。而针对多模式集成方法有集合平均法、消除偏差集合平均法、加权集成法、多模式最优评分集成法等，研究表明综合采用多种方法一起订正要优于采用单一方法的订正效果：如，利用频率匹配法先进行单模式订正后，再分别利用3种集成方法进行多模式集成，在强降水的落区预报和降水中心的量级预报效果优于原始多模式集成与单模式结果（智协飞和赵忱，2020）；利用逻辑回归方法、线性回归法先对4个模式降尺度订正，再将4个预报值进行消除偏差集合平均，结果多模式集成的预报效果优于单模式结果（王海霞和智协飞，2015）；利用最优TS评分分别订正欧洲中期天气预报中心（European Centre for Medium-Range Weather Forecasting， ECMWF）全球数值预报模式、中国气象局上海数值预报模式（China Meteorological Administration Shanghai 9 km， CMA-SH9）降水预报后，再利用降水分级最优化权重法对订正后的两种产品集成，集成预报在几乎所有预报时效、所有降水量级的TS评分均高于单一订正后的降水预报（危国飞等，2020）。以上研究表明，单模式的偏差订正、多模式集成方法均不同程度地提高了数值模式降水预报准确率，且多模式集成预报要优于单一模式的订正预报。

随着机器学习和人工智能理论与技术的不断发展，越来越多的深层次神经网络被提出并得到应用。这些深层次网络可以有效地处理大规模、高维度的数据，并具备处理复杂非线性关系的能力，应用效果往往优于依靠统计特征或者主观经验积累的传统方法（王在文等，2012；顾建峰等，2020；孙健等，2021；袁凯等，2023；袁雅涵等，2023）。如，采用卷积神经网络训练的逐时降水分级订正模型，与频率匹配法对比，降低了分类降水预报的漏报率和晴雨、弱降水预报的空报率（陈锦鹏等，2021）；利用ECMWF逐日24 h累积降水集合预报资料，分别建立了前馈神经网络（Neutral Network， NN）和带地理信息（Neutral Network-Geographic Information， NN-GI）模型进行概率预报，经NN和NN-GI模型订正后得到明显改进（智协飞等，2021）；基于人工树突神经网络（Artificial Dendritic Neural Network， ADNN）算法，针对CWRF模式（Climate-Weather Research and Forecasting mode）回报的1996—2019年夏季降水量进行订正，提高了该模式降水预测精度（李涛等，2022）。

以上各类机器学习人工智能方法与气象大数据结合，在强对流监测、短时临近预报、短期预报领域得到了广泛应用，但利用深度学习方法开展多模式集成降水预报研究较少。因此，本文采用深度前馈神经网络（Deep Forword Neural Networks， DFNN）和多模式降水分级最优TS权重集成方法，设计了4组DFNN方案和1组Mul-OTS（Multi-mode Optimal Threat Score）集成方案，对多模式集成降水预报进行客观订正研究，以期提高山东定量降水预报准确率。

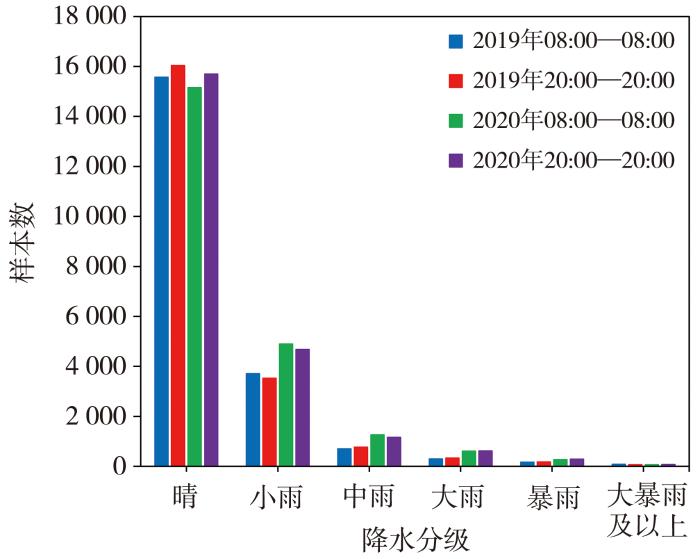
降水实况使用2019、2020年4—9月山东省123个国家级地面气象观测站（简称“国家站”）和298个区域级地面气象观测站（简称“区域站”）逐日24 h累积降水量。其中，2019年4—9月24 h累积降水量作为标签，用于DFNN降水预报模型训练和验证，以及对模式进行TS评分建立Mul-OTS集成模型；2020年4—9月24 h累积降水量用来对集成预报进行检验分析。文中所有时间均为北京时。图1为山东省123个国家站不同降水等级样本数，2019年晴样本数是小雨样本数的5倍左右，是中雨样本数的21倍左右，是暴雨以上等级样本数的64倍左右，不同降水等级训练样本极度不平衡。2020年小雨到暴雨样本数较2019年偏多，晴和大暴雨以上样本数则略少于2019年。

文中附图涉及地图是基于国家测绘地理信息局标准地图服务网站下载的审图号为GS（2017）3320号的标准地图制作，底图无修改。

数值预报降水资料包括中国气象局中尺度天气数值预报系统（China Meteorological Administration Mesoscale，CMA-MESO）72 h内逐24 h累积降水量，产品水平分辨率为10 km；中国气象局上海数值预报模式系统（CMA-SH9）72 h内逐24 h累积降水量，产品水平分辨率为9 km；欧洲中期天气预报中心（ECMWF）全球数值预报系统细网格72 h内逐24 h累积降水量，产品水平分辨率为0.125°×0.125°。以上资料研究时段均为2019、2020年4—9月，采用反距离权重插值法（李金洁和王爱慧，2019）将3个模式的逐24 h累积降水量预报降尺度生成水平分辨率为0.05°×0.05°的格点数据，然后提取自动站临近格点值和实况观测的24 h累积降水量进行空间匹配。

多模式降水分级最优TS权重集成（Mul-OTS）基本思想是对不同降水等级设置不同权重系数，使降水的TS评分在各降水等级达到最优（危国飞等，2020）。优点是在各降水等级上分别进行多模式权重集成，不同降水等级集成时的权重系数采用各模式对应降水等级TS评分权重比例。具体公式如下：

式中：yj（mm）为第j次迭代集成降水量预报；yj-1（mm）为第j-1次迭代集成降水量预报；N为模式集成个数；xi（mm）为第i个模式的降水量预报；Pk为第k个降水等级阈值，k取0~5时，对应Pk取0.0、0.1、10.0、25.0、50.0、100.0 mm；wik为第i个模式在不同k降水等级的权重系数，本文采用2019年4—9月3个模式24 h累积降水量的TS评分权重比例作为权重系数（图2）。由图2看出，中雨以上降水等级ECMWF的权重系数大于CMA-SH9和CMA-MESO。首次迭代y0采用3个模式的平均值，通过穷举法得到最优迭代次数j为2，最终建立Mul-OTS集成模型。

深度学习概念由Hinton等（2006）提出，属于统计学习范畴，本质是从数据出发，提取数据特征，发现数据中的联系，抽象出数据模型，最后回到数据分析与预测中。本文使用的深度学习方法为深度前馈神经网络DFNN结构（图3），主要分输入层、多个隐含层和输出层，相邻神经元的节点全部连接，各层之间没有反馈。

DFNN算法实现主要分两步，第一步通过“前向传播”将输入特征向量逐层映射提取数据特征，并利用前向传播的输出值和真值样本标签建立损失函数Loss；第二步利用误差“反向传播”算法最小化损失函数，使模型达到收敛状态，减少模型预测值的误差，不断调整优化权重W和偏置B得到DFNN模型。第一步前向传播公式如下（阿斯顿·张等，2019）：

式中：W为权重矩阵；B为偏置向量，Xi=Yi-1(i=1,2 ,⋯, n)，即当前神经元的输出特征向量Yi-1作为下一神经元的输入特征向量Xi；f⋅表示神经元的激活函数，使得神经网络可以任意逼近任何非线性函数，常用的激活函数有Sigmoid、Softmax、Tanh、Relu、Elu等。

第二步反向传播最小化损失函数，晴雨分类使用交叉熵函数（Cross Entropy Loss）。降水量回归使用均方误差（Mean Square Error，MSE）函数。损失函数公式（阿斯顿·张等，2019）如下：

式中：y（mm）表示站点观测降水量；y^（mm）表示训练模型预测降水量；m表示样本数。

降水预报检验采用气象系统业务常用办法，主要有平均相对误差（Mean Relative Error， ME）、晴雨准确率（Precision， PC）、TS评分、漏报率（Missing ratio， PO）、空报率（False Alarm Ratio， FAR）、预报偏差Bias及ETS（Equitable Threat Score）评分等（Jolliffe and Stephenson， 2003；王雨和闫之辉， 2007）^①(①国家气象中心, 2020. 智能预报技术方法竞赛检验方案.气预函〔2020〕34号.北京:中国气象局预报与网络司.)，主要公式如下：

式中：y(i)表示第i样本观测值；y^(i)表示第i样本预测值；m表示总样本数；ME表示训练模型对观测的拟合程度，越接近0说明预报和实况的偏差越小；NA、NB、NC分别为对应降水等级预报正确站数、空报站数、漏报站数；ND为预报和观测降水量均小于该降水等级的站数；Bias越接近1说明预报的降水面积和实况面积越接近，和降水位置无关，Bias>1表示存在湿偏差，Bias<1表示存在干偏差；ETS评分越接近1越好，并且对空报和漏报有惩罚，空报的影响大于漏报，ETS≤0表示预报为负技巧，ETS>0表示预报为正技巧。

各数值模式在分辨率、初始场、积分步长、物理参数化方案和动力框架等方面不同，各模式预报误差也不尽相同，如全球模式ECMWF对于大尺度系统性降水预报较好，但存在小雨空报较多，强降水偏弱等问题，而区域模式由于分辨率更高，同化本地资料更多，对对流性短时强降水预报更好，但空报较多。为考察多模式集成预报效果，本文通过对ECMWF、CMA-SH9和CMA-MESO数值模式进行不同组合，设计了4组DFNN方案（表1中方案1、2、3、4）和1组Mul-OTS集成方案（表1中方案5）进行对比研究。

用2019年4—9月模式24 h累积降水量作为DFNN方法的训练集训练模型。由于不同降水等级样本数存在明显数据不平衡（图1），导致训练模型获得的数据特征更多来自弱降水，损失了强降水的数据特征。然而，暴雨以上等级的预报往往需要重点关注，因此本文训练降水预报模型分为两个步骤：第一步训练晴雨二分类模型。训练分类模型之前数据进行随机下采样使晴、雨样本数相等，模型包含5个隐含层，节点数分别为32、64、128、64、16，输出层激活函数使用Sigmoid，损失函数使用交叉熵损失；第二步只用有降水的样本训练降水回归模型。模型包含3个隐含层，节点数分别为32、64、16，回归模型输出层不设激活函数，损失函数使用MSE损失。训练分类和回归模型时数据标准化均使用Z-score，激活函数均使用ReLu，优化损失函数均采用Adam梯度下降算法，损失函数正则化均使用L2-norm，初始化权重方法均采用随机初始化方法，随机取[-0.5，0.5]。

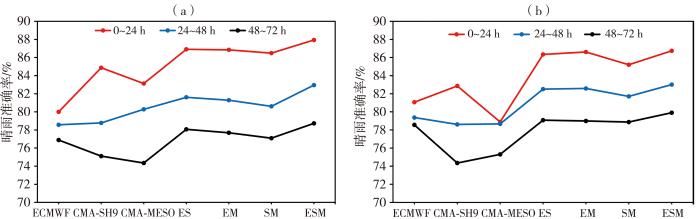
训练晴雨分类模型和降水回归模型均采用10次交叉验证策略评估模型的预测性能和泛化能力（图4）。通过对比，3个模式（ECMWF、CMA-SH9、CMA-MESO）08：00、20：00起报的0~24 h累积降水量预报，CMA-SH9晴雨准确率均最高，对应4组DFNN晴雨分类模型（ES、EM、SM、ESM）10次交叉验证晴雨准确率的平均值ESM方案均最高，分别提高了3.07%、3.88%，ES和EM方案基本相当，SM方案最低；3个模式24~48 h累积降水量预报，08：00起报的CMA-MESO晴雨准确率最高，20：00起报的ECMWF晴雨准确率最高，对应4组DFNN晴雨分类模型10次交叉验证晴雨准确率的平均值ESM方案均最高，分别提高了2.67%、3.64%；3个模式08：00、20：00起报的48~72 h累积降水量预报，ECMWF晴雨准确率均最高，对应4组DFNN晴雨分类模型10次交叉验证晴雨准确率的平均值ESM方案均最高，分别提高了1.84%、1.34%。因此，4组DFNN方案训练的晴雨分类模型在不同起报时间、不同预报时效相比模式预报均不同程度提高了晴雨准确率，随着预报时效的延长，提高的程度减少；用3个模式训练的ESM晴雨分类模型准确率提高最多，全球模式和区域模式相结合训练的ES和EM晴雨分类模型准确率相当，只用两个区域模式训练的SM晴雨分类模型准确率提高最少。

训练降水回归模型时仅使用了实况有降水样本进行训练，因此表2的检验结果去掉了2019年4—9月实况为晴的样本数。通过对比，不同起报时间、不同预报时效的3个模式逐24 h累积降水量预报，ECMWF平均相对误差（ME）均最低，说明实况在有降水发生时，ECMWF的降水预报效果最好。和模式预报相比，4组DFNN降水回归模型10次交叉验证的平均相对误差（ME）均小于模式预报，其中ESM方案最低。因此，4组DFNN方案训练的降水回归模型均改进了降水预报的效果，且4组DFNN方案当中，用3个模式训练的ESM降水回归模型平均相对误差（ME）最低，优于其他3组DFNN训练（ES、EM、SM）降水回归模型。

深度学习模型往往容易过拟合，为进一步评估DFNN降水模型的预报能力，使用2020年4—9月模式预报的逐24 h累积降水量作为测试集进行检验，并和Mul-OTS集成方法进行对比。由于3个数值模式水平分辨率不同，采用反距离加权插值方法将3个模式的逐24 h累积降水量预报降尺度生成水平分辨率为0.05°×0.05°格点数据，作为DFNN方法多模式集成预报的输入进行格点预报。具体步骤：将插值后的多模式格点数据首先输入到晴雨分类模型进行晴雨分类预报，无雨的格点预报为晴，有雨的格点预报再输入到降水回归模型输出定量降水格点预报，最终融合晴雨分类模型和降水回归模型的预报生成全场格点预报。检验时选取距123个国家站临近格点和观测匹配。

由表3看出，不同起报时间、不同预报时效，3个模式中，CMA-MESO平均相对误差ME均最小。具体地，CMA-MESO模式08：00、20：00起报的0~24 h累积降水量平均相对误差分别为0.34、0.37，对应ESM方案分别为0.25、0.24，分别降低了0.09、0.13，对应Mul-OTS方案分别为0.32、0.34，分别降低了0.02、0.03；CMA-MESO模式08：00、20：00起报的24~48 h累积降水量平均相对误差分别为0.41、0.40，对应ESM方案分别为0.29、0.30，分别降低了0.12、0.10，对应Mul-OTS方案分别为0.40、0.37，分别降低了0.01、0.03；CMA-MESO模式08：00、20：00起报的48~72 h累积降水量平均相对误差分别为0.44、0.42，对应ESM方案分别为0.35、0.32，分别降低了0.09、0.10，对应Mul-OTS方案分别为0.42、0.40，分别降低了0.02、0.02。总体上，5组集成方案的平均相对误差均小于3种模式，且ESM方案最好，Mul-OTS方案不如ES、EM、SM方案。

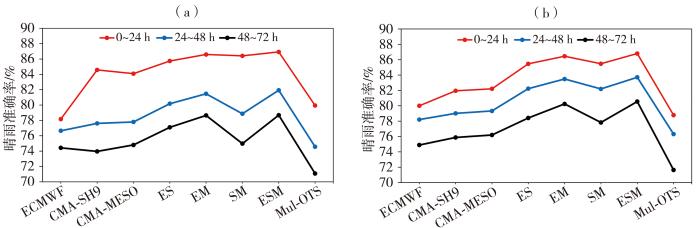
图5为不同模式和不同方案预报山东省不同预报时效的2020年4—9月逐24 h累积降水量晴雨准确率。可以看出，3个模式中，CMA-SH9模式08：00起报的0~24 h累积降水量晴雨准确率最高为84.58%，对应ESM方案为86.92%，提高了2.34%，Mul-OTS方案为79.94%，降低了4.64%；CMA-MESO模式20：00起报的0~24 h累积降水量晴雨准确率最高为82.21%，对应ESM方案为86.80%，提高了4.59%，Mul-OTS方案为78.78%，降低了3.43%；CMA-MESO模式08：00、20：00起报的24~48 h累积降水量晴雨准确率均最高，分别为77.80%、79.32%，对应ESM方案分别为81.93%、83.71%，分别提高了4.13%、4.39%，对应Mul-OTS方案分别为74.57%、76.31%，分别降低了3.23%、3.01%；CMA-MESO模式08：00、20：00起报的48~72 h累积降水量晴雨准确率也均最高，分别为74.80%、76.19%，对应ESM方案分别为78.68%、80.55%，分别提高了3.88%、4.36%，对应Mul-OTS方案分别为71.08%、71.64%，分别降低了3.72%、4.55%。总体上，不同起报时间、不同预报时效，4组DFNN方案相比模式预报均提高了晴雨准确率，且ESM方案最好，其次为EM方案，而Mul-OTS方案晴雨准确率低于模式本身预报。

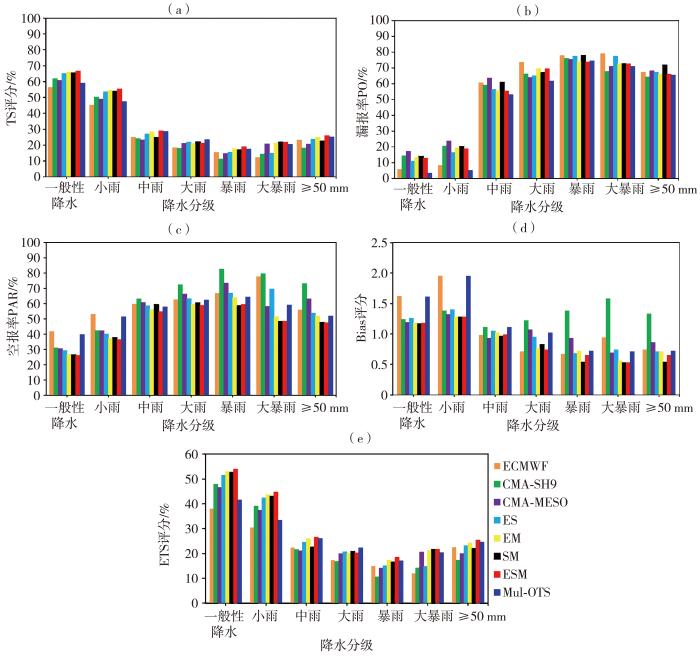
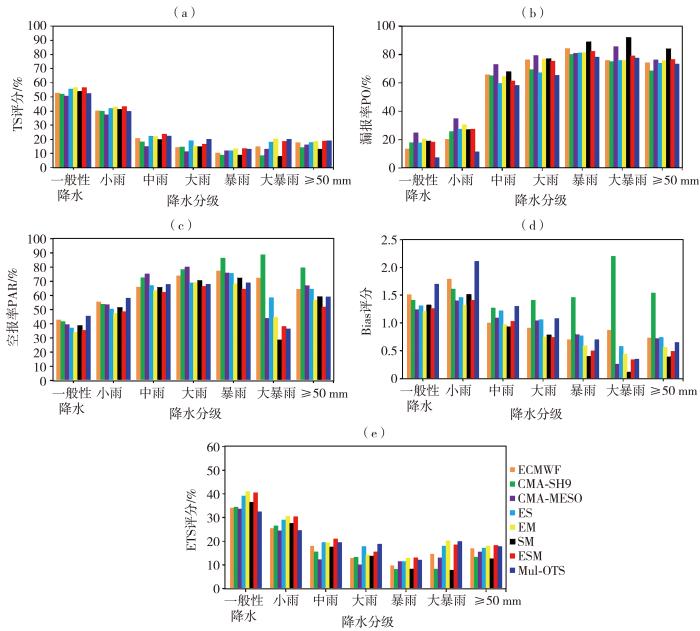
由于08：00、20：00起报的预报结论比较一致，以08：00起报为例，图6、图7分别为不同模式和不同方案预报2020年4—9月山东省0~24 h、24~48 h累积降水量的评分结果（一般性降水指小雨至大雨区间降水等级，≥50 mm指暴雨及以上降水等级）。由0~24 h累积降水量预报的评分结果（图6）看出，3个模式对比，全球模式（ECMWF）一般性降水和小雨漏报率较低、空报率较高，Bias评分大于1.5，具有明显的湿偏差，TS、ETS评分明显低于区域模式预报，大雨及以上降水等级漏报率较高，Bias评分小于1.0，具有干偏差；2个区域模式对比，中雨及以下降水等级TS、ETS评分CMA-SH9高于CMA-MESO，大雨及以上降水等级TS、ETS评分CMA-MESO高于CMA-SH9，CMA-SH9和CMA-MESO各降水等级漏报率相差不大，但CMA-SH9强降水空报率明显高于CMA-MESO，Bias评分大于1.3，具有明显的湿偏差。

5组集成方案对比，各降水等级TS、ETS评分趋势基本一致。一般性降水、小雨、中雨、暴雨和≥50 mm降水等级TS、ETS评分ESM方案均最高；大雨TS、ETS评分Mul-OTS方案最高，SM方案次之；大暴雨TS、ETS评分SM方案最高，ESM方案次之，ES方案最差，甚至不如CMA-MESO预报，但ES方案是ECMWF和CMA-SH9的集成结果，所以ES方案也是正效果。4组DFNN方案，中雨及以下等级的Bias评分比模式预报更趋近于1，大雨及以上等级的Bias评分小于1，低于模式预报，存在干偏差；Mul-OTS方案中雨以下等级具有明显的湿偏差，暴雨及以上等级是干偏差。4组DFNN方案相比模式空报率明显降低，漏报率略有改进，说明DFNN方案主要是通过降低空报率来提高各降水等级的TS、ETS评分，Mul-OTS方案漏报率明显降低，但空报率改进不大，小雨、一般性降水空报率反而变差。5组集成方案对大暴雨的改进虽然是正技巧，但提升不明显，因为大暴雨的训练样本较少，2019年4—9月08：00至次日08：00仅有86个样本（图1）。

24~48 h累积降水量的评分结果（图7）显示，SM方案暴雨、大暴雨和≥50 mm降水等级TS、ETS评分为负效果，Mul-OTS方案小雨、一般性降水的ETS评分也为负效果，其他各降水等级5组集成方案均提高了TS、ETS评分；虽然Mul-OTS方案中雨以下等级评分效果较差，但大雨、大暴雨等级的TS、ETS评分最高，优于DFNN方案，且暴雨及以上TS、ETS评分略低于ESM方案，和EM方案评分相当。

对于更长预报时效的48~72 h累积降水量评分结果（图略），4组DFNN方案对大雨及以下等级的TS、ETS评分仍然有明显提高，但暴雨等级的EM和SM方案，大暴雨等级的4组DFNN方案均为负效果；Mul-OTS方案对中雨以下、大暴雨等级的TS、ETS评分为负效果，对大雨的评分效果一般，但暴雨、≥50 mm降水等级TS、ETS评分和ESM方案评分相当。

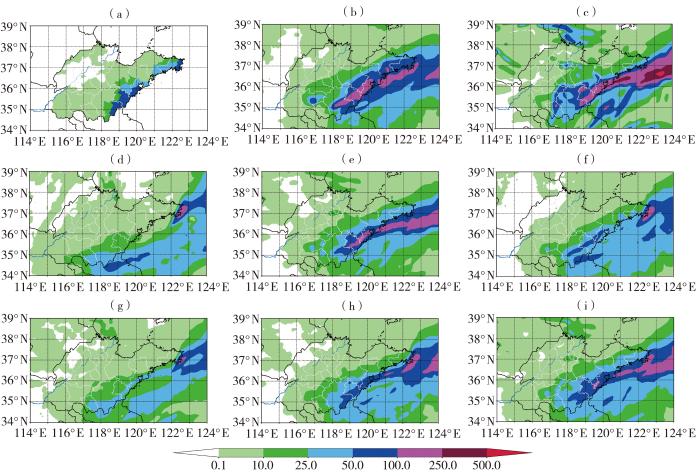
受高空槽和西南暖湿气流的共同影响，2021年8月22日下午至24日上午，山东南部自西向东出现了一次明显的强降水过程。对比实况观测（图8），从模式12~36 h累积降水量来看，3种模式及ES、SM、Mul-OTS方案对鲁西北晴雨空报范围都较大，SM、ESM方案虽然也有一定的空报，但比较接近实况；对鲁西南和山东半岛的强降水，ECMWF、CMA-SH9、ES和Mul-OTS预报降水强度偏强、范围偏大，CMA-MESO、EM和SM预报降水强度偏弱、降水落区偏差较大，而深度学习ESM方案较为准确地预报出强降水的落区和强度。总体上，这次降水过程，深度学习ESM方案最好。

为检验降水格点预报的整体预报性能，检验时增加了山东298个非训练区域站，共421个考核站检验结果。另外，由于数值模式的延时，业务上0~12 h时效的预报产品无法使用，用12~36 h、36~60 h累积降水量生成客观格点预报产品。经检验，晴雨预报准确率12~36 h和36~60 h累积降水量4种DFNN方案均高于模式预报[图9（a）、（b）]，ESM方案均最高，EM方案次之，而Mul-OTS方案最低，不如模式本身预报；12~36 h累积降水量预报ETS评分[图9（c）]，除大暴雨ES方案，其他4组DFNN方案均不同程度提高了各降水等级的ETS评分，对弱降水的提高幅度大于强降水，ESM方案最好，而Mul-OTS方案对中雨以上量级ETS均取得较好的订正效果，和ESM方案相当，但在一般性降水、小雨的ETS仍低于模式；36~60 h累积降水量预报ETS评分[图9（d）]，4组DFNN方案对大雨及以下等级的ETS评分仍然有明显提高，对较强降水也有一定改进，但暴雨等级的SM方案，大暴雨等级的ES和SM方案为负效果，Mul-OTS方案对中雨及以上量级ETS仍有一定效果，但明显不如ESM方案，甚至不如ES和EM方案。总之，加入非训练站点的检验结果表明采用有限站点建模降尺度生成格点预报有效。

为提高定量降水预报准确率，本文采用深度前馈神经网络DFNN和降水分级最优TS权重集成方法对多模式降水预报进行集成研究。使用2019年4—9月ECMWF、CMA-SH9和CMA-MESO逐24 h累积降水量，通过数据下采样、Z-score标准化、10次交叉验证，进行有监督训练得到4组DFNN（ES、EM、SM、ESM）晴雨分类和降水回归深度学习模型，其中晴雨分类模型包含5个隐含层，降水回归模型包含3个隐含层。以及利用多模式降水等级TS评分作为权重建立了Mul-OTS集成模型。分别用2020年4—9月3个模式逐24 h累积降水量进行降尺度格点预报，对5种集成方案对比分析，主要结论如下：

（1）不同起报时间、不同预报时效，5组集成方案的平均相对误差均小于3个模式，ESM方案最好，其次为ES、EM、SM方案，Mul-OTS方案最差，仅略好于模式预报。

（2）不同起报时间、不同预报时效，4组DFNN方案相比模式预报均提高了晴雨准确率，ESM方案最好，其次为EM方案，而Mul-OTS方案晴雨准确率低于模式预报，这是因为Mul-OTS方案小雨的空报率较高。虽然2020年4—9月模式晴雨准确率和用于训练的2019年4—9月模式晴雨准确率预报特征（均值和标准差）不同，但4组DFNN方案晴雨准确率仍取得较好预报效果。

（3）0~24 h累积降水量评分，4组DFNN方案均明显提高了各降水等级TS、ETS评分，对弱降水的提高幅度大于强降水；24~48 h、48~72 h累积降水量评分，4组DFNN方案对大雨及以下等级的TS、ETS评分有明显提高，对暴雨以上降水等级评分，除了个别方案为负技巧外，其他方案优于模式预报；Mul-OTS方案对小量级降水等级为负技巧，主要对大量级降水等级的订正效果较好，但总体上不如ESM方案。

通过5种集成方案对比检验、预报个例分析和业务应用的结果来看，采用基于前馈神经网络的ESM方案明显优于其他集成方案。但由于各降水等级的训练数据样本不平衡，本文采用晴雨分类和降水回归分步训练再融合的方式对大暴雨等级的预报还有待提高。后续可以通过增加模式种类，如中国气象局北京快速更新循环数值预报系统（China Meteorological Administration Beijing， CMA-BJ），或者通过增加与降水量相关性较高的预报因子，如地形、垂直速度和对流有效位能（Convective Available Potential Energy，CAPE）指数等，或者通过积累更多历史数据增加强降水的训练样本等方式从大数据中提取更具有物理意义的特征。从技术方法方面尝试采用卷积或循环神经网络来增加降水的时空信息，按照各降水等级采用多分类训练方式，期待进一步提高各降水等级评分，尤其是改进大暴雨以上等级的预报水平。