太阳辐射是驱动地表各类物理与生物化学过程的主要能量来源，也是陆地生态系统物质与能量交换的关键因子（李平等，2022；郭豫宾和张船红，2022）。地表接收的太阳总辐射包括直射辐射和散射辐射，其中直射辐射以平行光束直接照射地面，散射辐射则经空气分子、云滴及气溶胶等粒子散射后到达地表。散射辐射不仅关系到植物光能利用效率与生态系统碳收支（江晓东等，2017；陈之光等，2018），还影响建筑设计、遮阳工程和太阳能资源利用（姚万祥等，2014；李峥嵘等，2017）。已有研究表明，我国北方和西北地区以太阳直接辐射为主，南方地区散射辐射占比较高（于瑛等，2018）。因此，明确不同地区总辐射中直接辐射与散射辐射的比例及其变化特征具有重要意义。

受观测条件限制，我国辐射观测站点数量较少。现有的98个辐射观测站中仅17个具备散射辐射观测能力，且东部多于西部，平原多于山地（曹其梦等，2020）。在散射辐射观测数据缺乏的情况下，需通过直散辐射分离模型利用水平面总辐射推算散射辐射。Liu和Jordan（1960）提出了最早的直散辐射分离模型，此后研究者基于长期辐射资料构建了适用于不同区域的模型，通过建立散射分数（水平面散射辐射/总辐射）或散射率（水平面散射辐射/天文辐射）与气象要素之间的函数关系计算散射辐射，涉及晴空指数、日照百分率、温度、相对湿度和云量等多个因子。近年来，中国区域直散分离模型的适用性评价已取得一定进展，于瑛等（2018）基于15个典型台站数据比较9种代表性模型，指出各区域最优模型存在明显差异；北京（冯巍等，2015）、上海（李峥嵘等，2013）等地也开展了相关评估，为模型选择提供了依据。

随着地区气候条件、地理特征、工业化水平、能源需求及大气环境等因素的改变，太阳辐射特征也发生了变化，经典模型的适用性在部分区域有所下降（马年骏等，2016）。因此，基于当地辐射数据对模型参数进行再拟合成为重要研究方向。林伟和沈辉（2013）基于Liu-Jordan模型构建了广州地区的修正模型，周勇等（2022）则评估了不同气候区模型的适用性并对参数进行优化，为区域散射辐射计算提供参考。

太阳能作为重要的可再生能源，具有清洁、安全及资源广泛等优势（张东海等，2023）。光伏发电是其主要利用方式，光伏阵列斜面上的辐射量直接决定发电输出。因此，光伏发电工程关注不同朝向与倾角下斜面辐射的估算（吴贞龙等，2016；李芬等，2021）。由于缺乏斜面辐射直接观测，基于水平面辐射准确推算斜面辐射显得尤为重要，其中水平面直接辐射与散射辐射是必要输入项。关于斜面辐射模型精度评估、斜面辐射变化特征（王恩宇等，2019；李芬等，2020）及最佳倾角研究（李芬等，2015）已取得较多成果，但普遍依赖直射和散射辐射观测，因此在缺乏这类观测的区域斜面辐射计算研究仍相对不足。

甘肃位于我国西北内陆，地处黄土高原、青藏高原和蒙古高原交汇带（沙莎等，2024），是国家重要能源基地（刘宗瑞等，2025）。其中河西地区处于青藏高原北缘的中纬度地带，属于温带大陆性干旱气候区（王博等，2023），日照时数长、辐射强，是国内太阳能资源最丰富的区域之一（吴国栋等，2024），具有独特的光伏产业优势。近年来，省内光伏发电增长迅速，单日发电量可达1.08亿千瓦时，占全省日发电量的18%（王占东，2024）。但该区域仅布设三个太阳总辐射观测站，缺乏直射与散射辐射观测，限制了散射辐射及光伏发电特征研究的深入开展。基于此，本文利用甘肃榆中观测站的历史辐射资料对3种经典直散分离模型进行参数修正，并对修正结果进行评估。在此基础上，选取河西地区两个典型光伏电站（张掖及酒泉电站，均长期运行稳定、维护及时且仪器标定规范）对修正模型的斜面辐射计算精确度进行检验。进一步利用电站实测总辐射数据计算水平面直接辐射和散射辐射，进而推算斜面总辐射及发电功率，并对计算精度进行综合评估。准确计算水平面总辐射的直射和散射分量对辐射特征研究、电站功率模拟及业务运行具有重要意义。本文通过引入本地化参数修正提高直散分离模型的适应性，并验证了修正模型在斜面辐射和光伏功率计算中的有效性。研究旨在改善散射辐射观测缺乏地区的散射辐射计算效果，并提升模型在光伏斜面辐射计算中的应用效果。此外，研究结果还可为本地辐射特征分析和光伏发电技术中斜面辐射计算提供科学参考。

使用2004年1月至2021年12月甘肃省榆中站（35.87°N，104.14°E）及酒泉站（39.77°N，98.49°E）的日照时数及太阳辐射观测资料。榆中站太阳辐射资料包括水平面总辐射和散射辐射逐时数据，有效数据占总观测时段的98.4%；酒泉站的太阳辐射资料为水平面总辐射逐时数据，有效数据占总时段的97.9%。日照时数为日值观测资料，缺测及异常值用月均值进行插补。此外，使用2021年3月至2022年2月张掖（38.52°N，100.11°E）及酒泉（39.62°N，98.53°E）光伏电站的发电功率、水平面总辐射及气温观测数据。总辐射和气温来自电站内自动气象站，时间分辨率为15 min。质控后的数据资料剔除停电、限电、检修、仪器故障及缺测时段，张掖电站有效数据占总观测时段的87.4%，酒泉占86.6%，数据连续性较好。文中均为北京时。

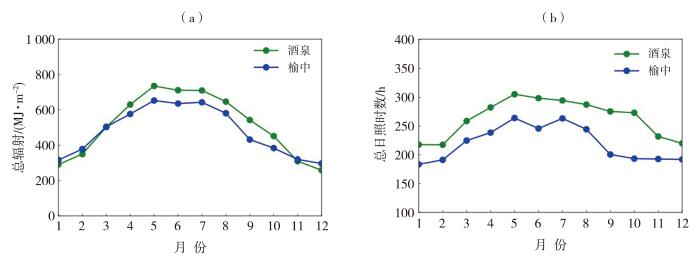
由于甘肃省辐射观测站点稀少，为验证利用榆中站辐射资料修正直散分离模型并应用于张掖和酒泉电站斜面辐射计算的合理性，对比分析了酒泉站与榆中站的辐射与日照气候特征（图1）。2004—2021年两站总辐射月际变化基本一致，均呈单峰结构：1月起逐渐增大，5月达到峰值，酒泉、榆中分别为735.0、652.8 MJ·m^-2，此后逐渐减小，至12月降至最低值（酒泉258.6 MJ·m^-2、榆中296.1 MJ·m^-2）；年际变化（图略）上，两站具有相似性，酒泉多年平均年总辐射量为6 137.1 MJ·m^-2，榆中为5 718.0 MJ·m^-2，两站均有9 a高于多年平均值，且辐射偏多或偏少的年份部分重合，尤其在2015—2021年均表现为持续偏高。日照时数的月际与年际变化特征也呈类似规律，酒泉多年平均年日照时数为3 169.5 h，榆中为2 634.3 h；两站月际变化均表现为1月起逐渐增大，夏季达到高值后逐渐回落；年际变化主要在多年平均值附近小幅波动，偏多和偏少年份亦存在一定一致性。

采用辐射气候学经验关系（Prescott，1940），以日照百分率（n/N）估算总辐射：

式中：I、I₀分别为总辐射和天文太阳辐射，单位均为MJ·m^-2；n、N分别为日照时数和可照时数，单位均为h；a₁、a₂为经验系数。可照时数和天文辐射按照GB/T 31155—2014《太阳能资源等级总辐射》（全国气象防灾减灾标准化技术委员会，2014）和GB/T 37526—2019《太阳能资源评估方法》（全国气候与气候变化标准化技术委员会风能太阳能气候资源分技术委员会，2019）中的公式计算。

晴空指数K_t计算公式如下：

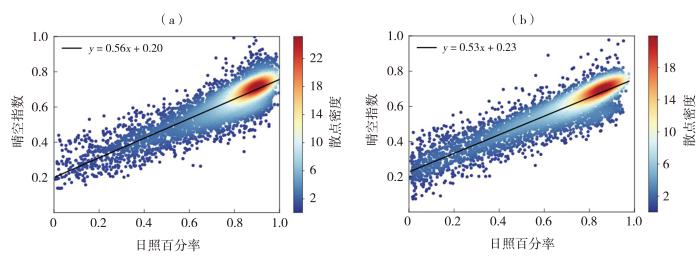
晴空指数与日照百分率的拟合关系及散点分布特征可反映云量、水汽和气溶胶等因素对辐射的综合影响（姚玉璧等，2023）。酒泉散点密集区域n/N∈[0.70,0.98]、K_t∈[0.55,0.80]；榆中散点密集区域n/N∈[0.65,0.95]、K_t∈[0.50,0.78]（图2）。两站K_t与n/N的拟合直线斜率接近，酒泉（斜率为0.56）略大于榆中（斜率为0.53），表明两地云层、水汽及气溶胶对太阳辐射的衰减特征具有相似性。

尽管酒泉与榆中在地理位置上存在一定距离，但两站均属西北干旱半干旱区，大尺度环流背景一致，均具有大气透明度高、日照时数长等典型大陆性气候特征，因而其辐射与日照变化规律明显相似。相比直接使用经典模型参数，榆中长期辐射观测数据更能精准反映区域太阳辐射特征，利用该资料修正直散辐射分离模型，并将其应用于张掖和酒泉电站的斜面辐射计算，具有较好的合理性和适用性。

首先对榆中站逐时总辐射与散射辐射数据进行质量控制。利用散射包络线法（Claywell et al.，2005）剔除异常值。具体步骤如下：1）计算散射辐射分数（Diffuse Radiation Fraction，DF，水平面散射辐射与总辐射的比值，简称“散射分数”）与晴空指数K_t，绘制二者的散点图，剔除超出[0,1]区间的异常数据；2）将K_t按其取值范围均分为10个数据带，对第m个数据带计算对应DF的平均值${\overline{\mathrm{D}\mathrm{F}}}_{m}$及标准偏差σ_m；3）将超出${\overline{\mathrm{D}\mathrm{F}}}_{m}$值±2σ_m的数据视为异常值，散射下包络线是10对（K_t，m，${\overline{\mathrm{D}\mathrm{F}}}_{m}$^－2σ_m）数据的二次拟合曲线，上包络线是10对（K_t，m，${\overline{\mathrm{D}\mathrm{F}}}_{m}$+2σ_m）数据的二次拟合曲线，K_t，m是第m个数据带中K_t的中值；4）未落入包络线区间的数据判定为异常并剔除。

利用榆中站观测资料得到的包络线表达式为

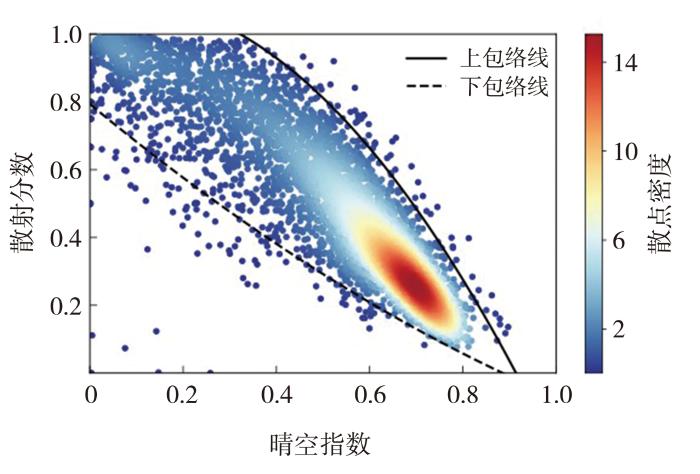
从散点密度分布（图3）可见，数据主要集中在K_t∈[0.5,0.8]、DF∈[0.1,0.6]区域，少量数据在包络线之外。质控后有效数据占观测时段的96.5%，可满足模型建模与检验需求。

选取3种典型直散分离模型Erbs模型、Orgill-Hollands模型与Liu-Jordan模型。三者参数易获取、应用广泛，具有代表性。

1）Erbs模型

基于晴空指数K_t的分段多项式模型，其表达式（Erbs et al.，1982）为

式中：ω为日落时角，单位为（°），计算方法参考国家标准GB/T 37526—2019（全国气候与气候变化标准化技术委员会风能太阳能气候资源分技术委员会，2019）。

2）Orgill-Hollands模型（简称“Orgill模型”）

基于K_t的线性分段模型，其表达式（Orgill and Hollands，1977）为

3）Liu-Jordan模型（简称“Liu模型”）

三次多项式模型，表达式（Liu and Jordan，1960）为

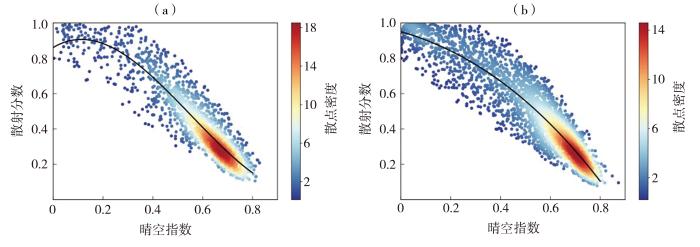
利用榆中站2004—2020年逐时水平面总辐射与散射辐射观测数据计算晴空指数K_t和散射分数DF，并基于二者的统计关系对典型直散分离模型进行本地化修正。图4为Erbs模型修正后2004—2020年榆中站不同日落时角K_t、DF的拟合曲线。修正后的Erbs模型表达式如下：

同样基于榆中站辐射资料，对Orgill模型与Liu模型的参数进行本地化修正，修正后的表达式分别为

Orgill模型：

Liu模型：

基于修正后的3种直散分离模型及光伏电站水平面总辐射观测数据计算得到水平面直接辐射和散射辐射，进一步利用Reindl各向异性模型计算光伏阵列斜面总辐射。该模型综合考虑环日辐射量、天空穹顶均匀散射及水平面亮度散射的地平分量，其表达式（Reindl et al.，1990）如下：

式中：I_tilt、I_b、I_d分别为斜面总辐射、水平面直接辐射、散射辐射，单位均为W·m^-2；ρ为地表反照率，一般取0.2；R_b为斜面直接辐射与I_b的比值；β为倾角，单位为（°）；A=I_b/I₀为各向异性指数，即直接辐射穿过大气的透光比；Z为太阳高度角，单位为（°）。

计算出斜面总辐射后，采用原理法（陈正洪等，2011）计算光伏输出功率。原理法基于光电转换效率与逆变器转换效率构建经验参数化模型，通过输入辐射数据计算得到光伏阵列直流功率，具体公式如下：

式中：P_dc为直流功率，单位为kW；NOCT为太阳能电池额定工作温度，T₀为气温，T_c为组件温度，单位均为℃；η为标准测试条件下的光电转换效率，单位为%；α为温度系数，单位为℃^-1；S为组件有效面积，单位为m²；k₁、k₂、k₃、k₄分别为光伏阵列老化损失、阵列失配损失、尘埃遮挡损失和直流线路损失系数；k₅为电站运行年限，单位为a；γ为太阳能电池材料年衰减率，单位为%。

为检验不同直散分离模型的修正效果及其对光伏发电功率估算的适用性，使用相关系数（Correlation coefficient，CORR）、平均绝对误差（Mean Absolute Error，MAE）、相对均方根误差（Relative Root Mean Square Error，RRMSE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）等统计指标进行综合评价（陈正洪等，2011）。

利用榆中站2021年总辐射和散射辐射观测数据，对模型修正前后的散射辐射计算结果进行检验（表1），结果表明，经过本地化修正后，各模型误差均有所降低，相关系数提升至0.89以上，说明修正后的模型能更好地反映区域辐射特性。

Erbs模型修正后MAE降低335.41 kJ·m^-2，Orgill模型、Liu模型修正后MAE分别降低211.39、823.76 kJ·m^-2；3种模型修正后的MAPE分别较原有模型降低6.72%、4.01%和9.65%，整体改进效果明显。

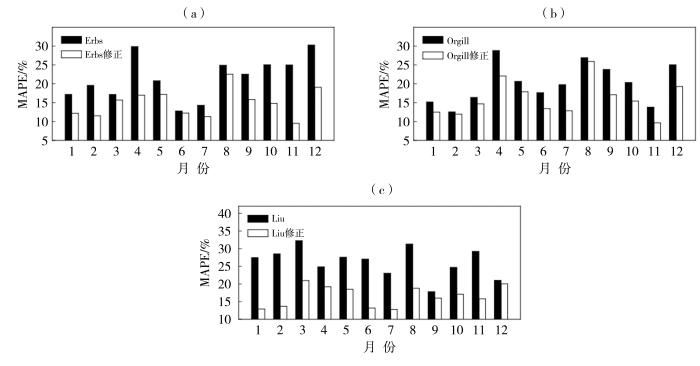
图5为3种模型修正前后榆中站2021年散射辐射的MAPE对比。可看出，3种模型修正后各月误差均有不同程度的降低，Erbs模型月均MAPE为12.78%~30.30%，修正后为9.52%~22.56%，其中11月改进最明显，MAPE降低15.47%；Orgill模型修正前后MAPE分别为12.56%~28.83%和9.66%~25.94%，改进幅度为0.61%~6.91%；Liu模型修正前后MAPE分别为17.82%~32.23%和12.77%~20.95%，改进幅度为0.99%~14.82%。

总体而言，3种直散分离模型修正后散射辐射计算精度均明显提升。Erbs修正模型的整体误差最低、相关性最高，性能优于另外两种模型。因此，在计算水平面散射辐射与直接辐射时，推荐优先采用Erbs修正模型。

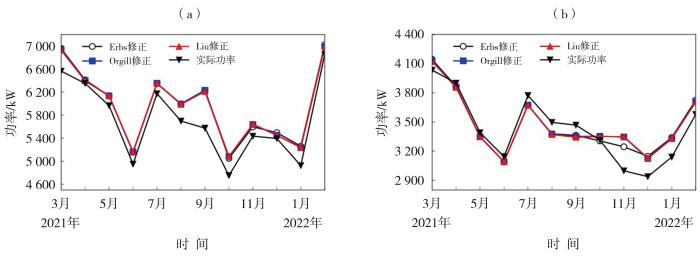
图6为张掖和酒泉电站实际发电功率与3种修正模型计算发电功率（简称“计算功率”）月均值的对比，3种修正模型计算得到的张掖电站月均发电功率能较为准确地描述实际发电功率的月变化趋势，模拟曲线与实况曲线吻合度较高。除9月计算值略高于实际值外（偏差为635.22 kW），其余月份偏差均较小，为42.88~364.93 kW，占实际发电功率的0.7%~5.6%，总体计算精度较高。

酒泉电站月均计算功率同样与实测值较为接近。除11月、12月和1月存在一定高估外（Erbs修正模型偏差为200.81~247.39 kW，占实际发电功率6.4%~8.3%），其他月份偏差为7.96~147.99 kW，占实际发电功率0.2%~4.1%，计算效果理想。

对比修正模型计算的光伏电站发电功率整体精度（表2），张掖和酒泉光伏电站实际发电功率与基于3种修正模型的计算功率相关系数均超过0.96，表明模型能够较好反映发电功率变化趋势。综合误差指标显示，Erbs修正模型表现最好，使用该模型得到的张掖电站计算功率的RRMSE、MAPE分别为5.38%和3.41%，酒泉电站分别为6.08%和4.39%，Erbs修正模型在两个电站均能达到较高的计算精度，适用于区域发电功率模拟研究。

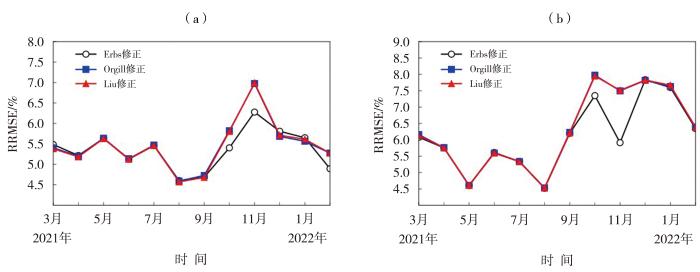
图7为张掖和酒泉电站3种修正模型计算功率月平均RRMSE对比。可看出，Erbs修正模型10、11月RRMSE明显低于另两种模型，其余月份3种模型差异较小。张掖电站Erbs修正模型的月均RRMSE为4.60%~6.28%，酒泉电站为4.52%~7.84%；Orgill模型与Liu模型修正后各月表现相近，张掖电站月均RRMSE为4.57%~6.99%，酒泉电站为4.53%~7.97%。Orgill模型与Liu模型利用实测数据直接修正多项式参数，未考虑其他因素的影响，因此两种模型修正后的计算性能接近。相比之下，Erbs模型依据水平面日落时角分段计算，能够体现太阳高度角变化对散射辐射的影响，因此修正后误差最低、相关性最好，且月际稳定性最强。

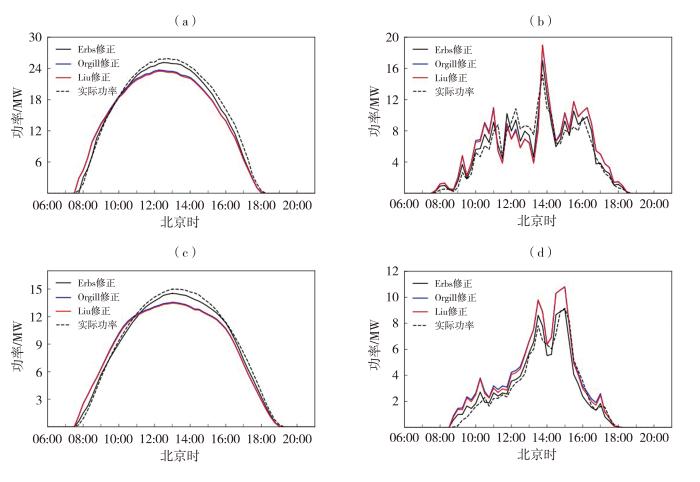
为进一步评估模型在更高时间分辨率下的适用性，选取模型差异最明显的2021年10—11月的晴天和多云天典型个例，分析张掖和酒泉电站计算功率与实际发电功率06：00—21：00的变化特征（图8）。晴天，计算功率呈平滑单峰结构，3种修正模型计算功率与实际发电功率均较为吻合，其中Erbs修正模型计算功率与实测发电功率最接近；多云天，计算功率波动变化，Orgill和Liu修正模型在不同时间段表现出不同程度的偏差，相比之下，Erbs修正模型计算功率与实际发电功率的整体偏差更小。

总体而言，3种修正模型均能较准确地计算光伏电站的斜面辐射及发电功率，月均发电功率与实测值接近，可用于斜面辐射研究及发电功率长时间序列分析。然而，从更高时间分辨率的模拟性能来看，Erbs修正模型误差最低、稳定性最好，并对发电功率日变化特点的把握也最准确，因此计算日尺度变化、15 min分辨率运行预测或进行短时发电功率模拟时，优先推荐使用Erbs修正模型。

基于甘肃省榆中站的历史辐射观测资料及张掖、酒泉光伏电站的运行数据，对3种典型直散分离模型进行参数修正，并将修正后的模型用于光伏阵列斜面辐射计算。通过对模型性能的系统评估，得出以下主要结论。

1）修正模型显著提升直散分离计算精度。修正后的Erbs、Orgill和Liu模型的MAPE分别较原模型下降6.72%、4.01%和9.65%，误差均明显降低。其中Erbs修正模型表现最好，能够更全面地呈现区域辐射特性。

2）3种修正模型计算的发电功率月均值均与实测结果高度一致。因此，在计算斜面辐射、分析发电功率月或年变化特征时，可根据需要任选其一。

3）Erbs修正模型计算功率整体误差最低，且在晴天及多云天均能准确再现实际发电功率日变化特征，计算功率与实测值更接近，在计算斜面辐射、分析发电功率的日变化特征或预测电站15 min发电功率时，优先推荐使用该修正模型。

本文基于现有资料初步对比分析了酒泉与榆中辐射月变化、年变化及与日照时数的关系，但两站之间的辐射差异可能还受到气溶胶、云量、水汽含量等因素影响，本文资料难以完全揭示其细节差异。后续研究需结合多源观测数据进一步验证修正模型在不同大气条件下的适用性。