基于ANUSPLIN软件的黑河流域降水空间插值方法研究

2.2 ANUSPLIN基本原理

ANUSPLIN软件使用薄盘光滑样条对多元噪声数据进行分析与插值，常用于分析气象数据。本文所使用的ANUSPLIN 4.37包含8个模块，分别为SPLINA、SPLINB、SELNOT、ADDNOT、DELNOT、GCVGML、LAPPNT、LAPGRD（Hutchinson，2007）。

SPLINA和SPLINB是ANUSPLIN的2个基本模块。SPLINA是使用FORTRAN 90编写的对多元噪声数据进行局部薄盘光滑样条插值的程序模块，适用于站点数小于2 000的情况，数据平滑度由广义交叉验证（Generalized Cross Validation， GCV）或最大似然法（Generalized Maximum Likelihood，GML）的最小化决定。SPLINB功能与SPLINA类似，针对更大的数据集（最多为10 000个站点）而设计，也可以应用于更小的数据集，能节省计算时间和存储空间，还可以用于提供更稳健的不良数据分析。SPLINB使用SELNOT选择初始节点，这些节点可以利用ADDNOT或DELNOT模块进行更新。GCVGML计算SPLINA和SPLINB所生成曲面的GCV或GML统计量，并将结果输出至文件以供检查与绘图。LAPPNT与LAPGRD分别在点或栅格上计算局部薄盘光滑样条曲面的值和贝叶斯标准误差估计。

局部样条模型可以表示为

（1）

z_{i} = f (x_{i}) + b^{T} y_{i} + e_{i} (i = 1, \dots, N)

式中： $z_{i}$ 为N个观察数据值， $x_{i}$ 为 $d$ 维样条独立变量， $f$ 为关于 $x_{i}$ 的未知光滑函数， $y_{i}$ 为 $p$ 维独立协变量，b为 $y_{i}$ 的 $p$ 维系数，T为迭代次数； $e_{i}$ 为期望值为0且方差为 $w_{i} σ^{2}$ 的自变量随机误差， $w_{i}$ 为相对误差方差（已知）， $σ^{2}$ 为误差方差，在所有数据点上为常数，但通常是未知的。该模型没有协变量（ $p = 0$ ）时简化为普通的薄盘样条模型， $f (x_{i})$ 不存在时为简单的多元线性回归模型。

2.3 插值模型对比与优选

ANUSPLIN通常至少有2个独立样条变量，即经度和纬度；第3个独立变量为海拔高度，通常用于拟合表面温度和降水，单位为km。在某些区域，有时可以将高程作为独立的协变量来提高完成度，如在拟合温度曲面时，协变量海拔的系数可能是经验温度递减率（Hutchinson，1991）。若能确定影响气候变量的其他因素并获得相关数据，可将其作为额外的协变量加入。样条次数最小为2。变量转换分为无转换、自然对数转换、平方根转换和发生转换。自然对数和平方根转换可以减少测量值的正偏态，适用于拟合自然非负数据。发生转换是将所有正数值设置为1.0，忽略所有负数值。Hutchinson（1998）发现在拟合薄盘光滑样条之前对日降雨量数据进行平方根转换，可将插值误差降低10%。

本研究拟采用独立样条变量个数、协变量个数、样条次数、变量转换方法等多种组合的27个薄盘光滑样条函数模型，利用SPLINA模块对2019年黑河流域12个月降水量数据进行插值实验（表2）。ANUSPLIN在日志文件中提供了一系列用于判别误差来源和诊断插值质量的统计参数，如均值（MEAN）、标准差（Standard Deviation，STDDEV）、拟合曲面参数的有效数量估计信号自由度（SIGNAL）、剩余自由度（ERROR）、平滑参数（RHO）、方差估计（Data Error Variance Estimate，VAR），广义交叉验证（GCV）、均方残差（Mean Square Residual，MSR）、期望真实均方误差（Mean Square Error，MSE）及其平方根RTGCV、RTMSR、RTMSE等。其中，模型质量主要由广义交叉验证（GCV）进行评估，GCV或RTGCV是对总体标准预测误差的保守估计，包含了估计数据误差。MSE是去除估计数据误差后的标准误差估计值。当平滑参数（RHO）过小时，SIGNAL可能达到最大值（等于SPLINA的数据点数或SPLINB的节点数）；当平滑参数（RHO）过大时，SIGNAL可能降至最小（取决于独立变量个数和粗糙惩罚阶数），这两种情况都表示曲面拟合过程未能找到最优平滑参数，在输出日志文件中用“*”标记（Hutchinson，2007）。Hutchinson和Gessler（1994）建议SIGNAL不超过站点数的一半，大于该值则表示数据量不足或存在数据误差正相关的问题。

表2 27个薄盘光滑样条函数模型

Tab.2 The 27 thin plate smoothing splines function models

序号	模型名称	独立变量	协变量	样条次数	变量转换	序号	模型名称	独立变量	协变量	样条次数	变量转换
1	V2S2	经度、纬度	—	2	—	15	V3S4_LOG	经度、纬度、高程	—	4	对数
2	V2S3	经度、纬度	—	3	—	16	V3S2_RT	经度、纬度、高程	—	2	平方根
3	V2S4	经度、纬度	—	4	—	17	V3S3_RT	经度、纬度、高程	—	3	平方根
4	V2S2_LOG	经度、纬度	—	2	对数	18	V3S4_RT	经度、纬度、高程	—	4	平方根
5	V2S3_LOG	经度、纬度	—	3	对数	19	V2C1S2	经度、纬度	高程	2	—
6	V2S4_LOG	经度、纬度	—	4	对数	20	V2C1S3	经度、纬度	高程	3	—
7	V2S2_RT	经度、纬度	—	2	平方根	21	V2C1S4	经度、纬度	高程	4	—
8	V2S3_RT	经度、纬度	—	3	平方根	22	V2C1S2_LOG	经度、纬度	高程	2	对数
9	V2S4_RT	经度、纬度	—	4	平方根	23	V2C1S3_LOG	经度、纬度	高程	3	对数
10	V3S2	经度、纬度、高程	—	2	—	24	V2C1S4_LOG	经度、纬度	高程	4	对数
11	V3S3	经度、纬度、高程	—	3	—	25	V2C1S2_RT	经度、纬度	高程	2	平方根
12	V3S4	经度、纬度、高程	—	4	—	26	V2C1S3_RT	经度、纬度	高程	3	平方根
13	V3S2_LOG	经度、纬度、高程	—	2	对数	27	V2C1S4_RT	经度、纬度	高程	4	平方根
14	V3S3_LOG	经度、纬度、高程	—	3	对数

注：“—”表示不取值。

最佳模型判断标准为GCV或RTGCV最小，SIGNAL小于站点数N的1/2，无“*”指示，SIGNAL与节点数（KNOTS）比值（S：NK）为0.20~0.80（Macdonald et al.，2021）。

2.4 站点数量敏感性实验

由于黑河流域气象与水文站点较少，且不同数据收集渠道也不同，为明确站点数量对降水量插值精度的影响，本研究拟利用SPLINA模块分别对黑河流域19个气象站点和26个水文站点2019年12个月降水量数据进行插值。并以5个站点为间隔数，利用SELNOT模块选用15、20、25、30、35、40、45个站点，SELNOT模块对独立样条变量空间进行等距采样，选取指定数量的站点作为节点集，大小约为数据集的1/4到1/3，所需的节点数取决于被拟合数据的空间复杂度，更多的节点用于更复杂的表面。再利用SPLINB模块对不同站点数量的降水数据进行插值，输出数据列表和拟合值，并计算SIGNAL与KNOTS比值，S：NK为0.20~0.80认为可接受，对比分析结果选取能代表流域降水真实值的最适宜站点数。

2.5 DEM分辨率敏感性实验

以分辨率分别为1 000、500、250、90 m的DEM高程数据作为变量，将优选模型的降水量曲面系数文件和误差协方差矩阵输入LAPGRD模块，生成栅格局部薄盘光滑样条曲面的值和贝叶斯标准误差估计，对比分析不同高程降水量插值的平均误差（Mean Error，ME）与标准误差（Standard Error， SE）。

3 结果与分析

3.1 不同模型插值结果

根据日志文件，分别统计每个薄盘光滑样条函数模型计算的12个面的统计数据平均值，变量转换的数据统计为近似的未转换数据值。通过对比27个薄盘光滑样条函数模型（表3），发现V3S4_LOG模型因节点数不足而无法运行，显示“TOO FEW KNOTS”，其余模型均成功输出插值结果。变量对数转换的模型KNOTS均值约为40，而变量不转换或变量平方根转换的模型KNOTS均值约为45，变量对数转换的模型筛选去除的站点数更多，独立变量为经度、纬度和海拔，样条次数为4的情况下，SPLINA筛选的站点数可能更少，导致模型运行出错。按照最佳模型判断标准，去除带“*”模型后，对比剩余V2S3、V2S4_LOG、V2S3_RT、V2S4_RT、V3S3、V2C1S3、V2C1S4、V2C1S4_LOG、V2C1S3_RT 9个模型，引入高程变量模型（编号10~27）的RTGCV较普通的薄盘样条模型（编号1~9）的RTGCV小，表明高程的引入有效减小了估计数据误差，V2C1S3_RT模型的RTGCV与RTMSE均最小，分别为6.10和4.82 mm，且S：NK均为0.20~0.80，拟合效果最优。因此，最优参数设置如下：独立变量为经度与纬度，协变量为海拔，样条次数为3，变量转换方式为平方根。

表3 27个薄盘光滑样条函数模型输出统计

Tab.3 Output statistics of 27 thin plate smoothing splines function models

编号	模型名称	KNOTS	SIGNAL	S：NK	RTGCV/mm	RTMSE/mm
1	V2S2	45	14.3（1个超过N的一半，2个带*）	0.31（1个超过0.80）	12.60	5.86
2	V2S3	45	12.3（1个超过N的一半）	0.27	13.20	5.90
3	V2S4	45	14.6（1个超过N的一半，3个带*）	0.32	13.70	6.38
4	V2S2_LOG	40	24.1（5个超过N的一半，4个带*）	0.60（4个超过0.80）	11.20	4.28
5	V2S3_LOG	40	19.3（3个超过N的一半，2个带*）	0.48（2个超过0.80）	13.90	5.82
6	V2S4_LOG	40	16.1（1个超过N的一半）	0.40	16.10	6.55
7	V2S2_RT	45	19.2（3个超过N的一半，1个带*）	0.43（1个超过0.80）	10.90	5.12
8	V2S3_RT	45	15.5（1个超过N的一半）	0.34	12.10	5.69
9	V2S4_RT	45	16.8（1个超过N的一半）	0.37	12.50	5.83
10	V3S2	45	23.2（5个超过N的一半，3个带*）	0.52（3个超过0.80）	5.40	7.08
11	V3S3	45	17.7（3个超过N的一半）	0.38	6.78	8.52
12	V3S4	45	23.0（7个超过N的一半，7个带*）	0.51	6.12	8.43
13	V3S2_LOG	40	35.6（11个超过N的一半，9个带*）	0.89（8个超过0.80）	1.58	1.43
14	V3S3_LOG	40	20.8（6个超过N的一半，2个带*）	0.52（2个超过0.80）	6.34	5.31
15	V3S4_LOG	—	—	—	—	—
16	V3S2_RT	45	29.9（6个超过N的一半，5个带*）	0.66（5个超过0.80）	3.53	3.29
17	V3S3_RT	45	19.6（2个超过N的一半，1个带*）	0.44（1个超过0.80）	5.63	4.40
18	V3S4_RT	45	23.5（4个超过N的一半，4个带*）	0.52（1个超过0.80）	5.24	5.15
19	V2C1S2	45	18.7（2个超过N的一半，2个带*）	0.42（2个超过0.80）	6.44	7.89
20	V2C1S3	45	16.9（2个超过N的一半）	0.38	7.07	8.53
21	V2C1S4	45	17.3（2个超过N的一半）	0.38	7.00	8.60
22	V2C1S2_LOG	40	27.1（8个超过N的一半，5个带*）	0.68（5个超过0.80）	3.52	3.60
23	V2C1S3_LOG	40	19.1（4个超过N的一半，1个带*）	0.48（1个超过0.80）	6.87	5.60
24	V2C1S4_LOG	40	17.0（2个超过N的一半）	0.43	8.25	6.11
25	V2C1S2_RT	45	20.5（3个超过N的一半，1个带*）	0.46（1个超过0.80）	5.27	4.26
26	V2C1S3_RT	45	18.1（2个超过N的一半）	0.40	6.10	4.82
27	V2C1S4_RT	45	17.2（1个超过N的一半，1个带*）	0.38	7.18	5.09

注：“—”表示数据缺失。

3.2 不同站点数插值结果

对比气象站点，将水文站点降水数据输入薄盘光滑样条函数模型得到的结果更加准确，2个带“*”，S：NK为0.27~0.48。而气象站点12个月降水拟合面中，11个超过站点数N的一半，5个带“*”，RTGCV最大为12.60 mm，表明大多数曲面拟合过程找不到最优平滑参数。利用SELNOT模块选取不同数目站点数，站点数越多，模型RTGCV越小，当站点数从19个增加至40个时，RTGCV与RTMSE均达到最小值，RTGCV从12.60 mm降至6.09 mm，降幅51.6%，RTMSE从5.50 mm降至4.81 mm，降幅12.5%，12个面中仅有2个面SIGNAL超过站点数N，且S：NK为0.27~0.74。而站点数进一步增加至45个时，RTGCV与RTMSE均略有上升（表4），这一现象可能与流域地形复杂度及站点空间分布均匀性有关。因此，选取40作为最适宜站点数。

表4 不同站点数降水数据运行V2C1S3_RT模型输出统计

Tab.4 Output statistics running V2C1S3_RT model with precipitation data from stations with different numbers

站点	N	KNOTS	SIGNAL	S：NK	RTGCV/mm	RTMSE/mm
气象站点	19	19	13.3（11个超过N的一半，5个带*）	0.70（4个大于0.80）	12.60	5.50
水文站点	26	26	9.4（2个带*）	0.36	6.82	5.32
15个站点	45	15	11.0（2个带*）	0.73（5个大于0.80）	8.31	5.04
20个站点	45	20	14.8（1个超过N的一半，1个带*）	0.74（3个大于0.80）	7.50	5.02
25个站点	45	25	16.9（1个超过N的一半，1个带*）	0.68（2个大于0.80）	6.50	4.99
30个站点	45	30	17.7（2个超过N的一半，1个带*）	0.59（1个大于0.80）	6.16	4.81
35个站点	45	35	17.9（2个超过N的一半）	0.51（1个大于0.80）	6.13	4.81
40个站点	45	40	18.1（2个超过N的一半）	0.45	6.09	4.81
45个站点	45	45	18.1（2个超过N的一半）	0.40	6.10	4.82

从表5可以看出，选取40个站点时，12个月降水量拟合面的RTGCV均值为6.09 mm，是对总体标准预测误差的保守估计，包含了程序估计的数据误差，12个月降水量拟合面的RTMSE为4.81 mm，是去除估计数据误差后的标准误差估计值。3月和6月降水量拟合面的SIGNAL大于站点数45的一半，利用SELNOT模块选择站点；当选择15个站点数时，3月降水量拟合面SIGNAL为11.9，小于站点数的一半，S：NK为0.79，符合要求，6月降水量拟合面SIGNAL为13.3，小于站点数的一半，S：NK为0.89，大于0.80，不符合要求；当选择20个站点数时，6月降水量拟合面SIGNAL为14.4，小于站点数的一半，S：NK为0.72，小于0.80，符合要求（表6）。

表5 40个站点2019年12个月降水数据运行V2C1S3_RT模型输出统计

Tab.5 Output statistics running V2C1S3_RT model with precipitation data in 12 months in 2019 from 40 stations

月份	N	KNOTS	SIGNAL	S：NK	MEAN/mm	RTGCV/mm	RTMSE/mm
1	45	40	17.3	0.43	4.86	3.50	1.66
2	45	40	18.6	0.47	2.95	2.38	1.14
3	45	40	23.5	0.59	1.61	1.31	0.64
4	45	40	16.5	0.41	22.90	8.62	4.13
5	45	40	22.1	0.55	40.40	11.80	5.88
6	45	40	29.5	0.74	73.60	17.00	8.06
7	45	40	12.9	0.32	52.80	13.90	6.25
8	45	40	15.0	0.38	40.80	12.40	5.83
9	45	40	15.0	0.38	57.70	15.80	7.41
10	45	40	11.8	0.30	21.10	9.32	4.06
11	45	40	18.9	0.47	10.10	6.95	3.36
12	45	40	15.6	0.39	2.68	2.23	1.03
平均	45	40	18.1	0.45	22.50	6.09	4.81

表6 不同站点数2019年3月和6月降水数据运行V2C1S3_RT模型输出统计

Tab.6 Output statistics running V2C1S3_RT model with precipitation data in March and June 2019 from stations with different numbers

月份	N	KNOTS	SIGNAL	S：NK	MEAN/mm	RTGCV/mm	RTMSE/mm
3	45	15	11.9	0.79	1.61	2.40	0.979
6	45	20	14.4	0.72	73.50	20.50	9.520

3.3 不同分辨率DEM插值结果

从表7可以看出，不同分辨率DEM对插值结果的影响较小。降水量预测值与实测值误差相差不大，平均误差为9.28~9.57 mm，标准误差为2.67~2.71 mm，平均误差与标准误差差异不足3.29%。其中，分辨率为1 000 m的DEM高程数据为协变量进行薄盘光滑样条插值后的降水量ME和SE最小，略优于更高分辨率数据，可能因更高分辨率DEM（如90 m）引入局部地形噪声，而1 000 m分辨率更契合流域宏观地形梯度，表明适度的DEM分辨率（1 000 m）更有利于平衡计算效率与精度。

表7 不同分辨率DEM降水量插值误差统计

Tab.7 Error statistics of precipitation interpolation with DEM of different resolutions

DEM/m	ME/mm	SE/mm
1 000	9.28	2.67
500	9.28	2.68
250	9.48	2.70
90	9.57	2.71

3.4 降水量空间分布特征与误差分析

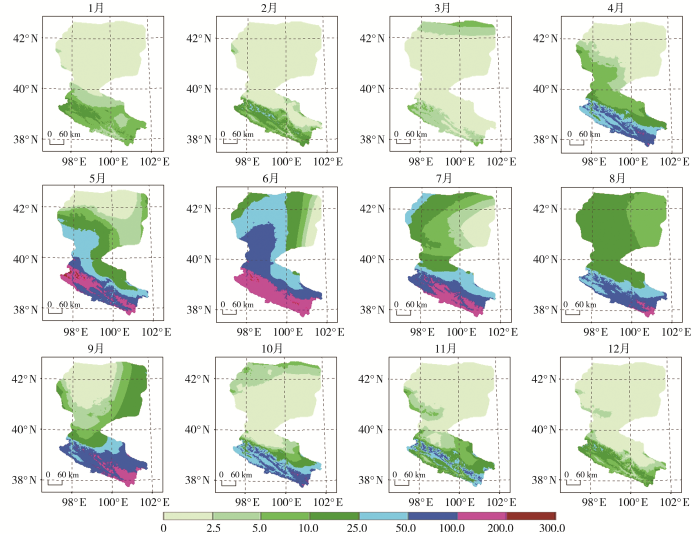
使用最优插值模型生成2019年黑河流域月降水量栅格数据。最优模型参数如下：独立变量为经度与纬度，协变量为海拔，样条次数为3，变量转换方式为平方根，站点数为40，DEM分辨率为1 000 m。在此基础上，利用ArcGIS平台将12个月的降水量栅格数据进行累加，得到年降水量栅格数据，并计算其像元平均值。2019年黑河流域平均降水量为211.39 mm，空间上自西南向东北递减（图2），与祁连山地形抬升效应一致。西南上游高海拔区（海拔>4 000 m）平均降水量达380.00 mm，而东北下游戈壁区（海拔<1 000 m）仅82.00 mm。1、2、3、12月降水量较少，月平均降水量分别为1.76、2.80、1.49、2.71 mm，降水量SE也较小。其中，3月降水量最少，仅有0.05~8.34 mm；自4月起，降水量超过25.00 mm的区域自西南向东北扩大；5月降水量大幅增加，月平均降水量为32.66 mm；汛期6—9月降水量较多，月平均降水量分别为56.48、29.63、24.05、26.84 mm，其中，6月降水量最大（0.13~238.00 mm），全流域降水量超过25.00 mm的区域占比最大（72.11%）；之后，全流域降水开始逐渐减少，10、11月平均降水量分别为11.64、7.26 mm。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 2019年黑河流域月均降水量（单位：mm）分布

Fig.2 Distribution of monthly average precipitation （Unit： mm） in the Heihe River Basin in 2019

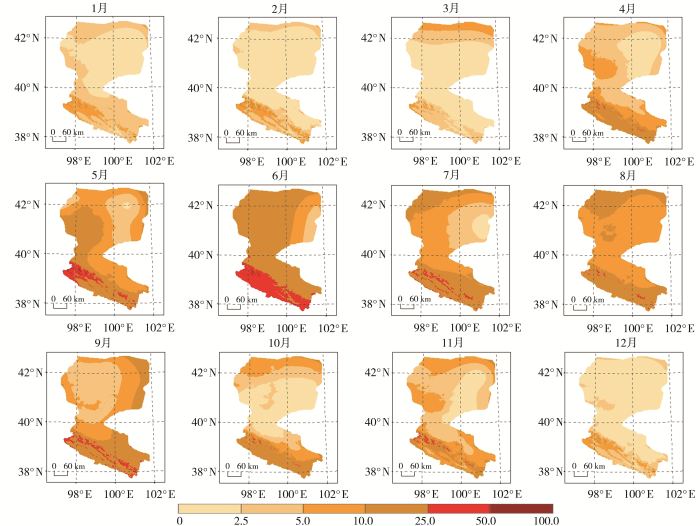
2019年黑河流域平均降水量SE为0.54~72.23 mm。降水量SE空间分异明显，黑河上游特别是上游西南地区SE较大，下游边界地区降水量SE较相邻地区大，主要是因为该区域气象和水文站点较少。1、2、3、12月降水量SE较小，为0.54~19.20 mm；5月降水量SE最大（72.23 mm）；汛期6—9月降水量SE较大，其中6月降水量最多，SE≥25.00 mm的区域占比最大（14.81%），主要集中在降水量≥100 mm的区域。汛期6—9月降水量高值区（≥100 mm）的SE普遍高于非汛期，表明极端降水事件的插值不确定性更高。10、11月降水量SE≥10.00 mm的区域较汛期减少，但较降水量较少的1、2、3、12月大（图3）。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 2019年黑河流域月均降水量标准误差（单位：mm）分布

Fig.3 The distribution of SE of monthly average precipitation in the Heihe River Basin in 2019 （Unit：mm）

4 结论与讨论

本研究在黑河流域结合气象与水文站点降水数据，利用ANUSPLIN软件构建局部薄盘光滑样条插值模型，探讨模型参数、站点数量及地形协变量对插值精度的影响，得出以下具体结论。

1）通过对比27个薄盘光滑样条函数模型，发现V2C1S3_RT模型（独立变量为经度、纬度，协变量为海拔，样条次数为3，变量转换方式为平方根）的插值精度最优。该模型的RTGCV和RTMSE均最小，分别为6.10和4.82 mm，信号自由度（SIGNAL）与节点数（KNOTS）比值（S：NK）为0.40，符合理论要求，表明其能够有效平衡模型复杂度与拟合精度。

2）站点数量显著影响插值误差，当站点数从19个（气象台站）增加至40个（联合气象台站与水文站）时，RTGCV从12.60 mm降至6.09 mm，降幅达51.6%。但站点数超过40后，误差指标RTGCV与RTMSE趋于稳定，表明40个站点是黑河流域降水插值的最优数据密度阈值。此外，水文站点数据的引入显著降低了插值误差，较单独使用气象台站数据RTMSE降低12.5%，验证了多源数据融合的有效性。

3）1 000、500、250与90 m等不同分辨率的DEM对降水量插值结果影响较小，平均误差与标准误差差异不足3.2%。但1 000 m分辨率DEM的插值误差略优于更高分辨率数据，ME与SE分别为9.28、2.67 mm，表明在复杂地形区，适度的DEM分辨率（1 000 m）更有利于平衡计算效率与精度。

4）2019年黑河流域平均降水量为211.39 mm，空间上自西南向东北递减，上游西南部及下游边界区域降水量SE显著高于其他区域，主要原因是该地区站点数较少。汛期6—9月降水量高值区（≥100 mm）的SE普遍高于非汛期，表明极端降水事件的插值不确定性更高。

本研究首次在黑河流域联合气象与水文站点数据，构建了基于ANUSPLIN的多源数据融合插值模型，为干旱区内陆河降水空间化提供了新范式。同时，量化了样条次数、变量转换方式对插值精度的敏感性，明确了最优参数组合，提出的“40站点阈值”和“1 000 m DEM优选”结论可直接应用于黑河流域的水文模拟与水资源管理，具有较高的应用价值。筛选的最优模型不仅其RTGCV较普通的薄盘样条模型显著降低，表明引入高程有效减小了估计数据误差；而且相较于单独使用气象台站数据，其RTMSE降低了12.5%，验证了多源数据融合在弥补西北内陆河等缺资料区数据不足方面的有效性。本研究仍存在以下不足：1）数据源局限于45个站点，未来可结合卫星降水产品（如GPM、TRMM）进一步优化；2）未考虑坡度、坡向等地形变量对插值的潜在影响；3）模型对极端降水事件的适应性需进一步验证。后续研究可尝试引入机器学习算法（如随机森林）与ANUSPLIN耦合，构建多模型融合框架，以提升复杂气候区的降水插值准确性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

耿蔚, 张亮, 杨进,

2019.

基于GIS的四川省区域性暴雨降水分布的空间插值方法与面积估测

[J]. 高原山地气象研究, 39(3): 75-81.

[2]

韩艳莉, 于德永, 陈克龙, 等,

2022.

2000—2018年青海湖流域气温和降水量变化趋势空间分布特征

[J]. 干旱区地理, 45(4): 999-1 009.

青藏高原是全球气候变化的敏感区,气温和降水量的空间分布及变化趋势是气候变化研究的核心和基础,为开展生态环境变化评估提供基础资料。基于2000—2018年青海湖流域及其周边气象站观测数据,以高程为协变量,结合专业气象插值软件ANUSPLIN对气温和降水量进行空间插值。利用线性回归法分析了青海湖流域2000—2018年气温和降水量的变化趋势;利用双变量空间自相关分析法分析了青海湖流域气温和降水量空间匹配关系。结果表明：（1） 2000—2018年青海湖流域年平均气温呈显著增加趋势,平均增速为0.30 ℃·（10a）-1,春季增温显著。（2）降水量呈显著增加趋势,平均增速为73.20 mm·（10a）-1,春夏季增速显著、秋季变化不明显、冬季趋于变干。（3）青海湖流域气温和降水量空间匹配差异显著。从年尺度来看,气温和降水量莫兰指数（Moran’s I）为-0.66,表现为显著的负相关,面积比为67.56%,水热组合空间匹配不佳。从季节尺度来看,青海湖流域春季、夏季、秋季和冬季的气温和降水量Moran’s I分别为-0.49、-0.80、-0.32和-0.14,均为空间负相关。春夏季,流域低海拔区域气温逐渐升高,高海拔区域降水量逐渐增多,气温和降水量空间负相关面积逐渐增大,水热组合空间匹配不佳。值得强调的是青海湖巨大水体对环湖区局地气温的调节作用明显,是青海湖流域的“气候调节器”。

[3]

施雅风, 沈永平, 胡汝骥,

2002.

西北气候由暖干向暖湿转型的信号、影响和前景初步探讨

[J]. 冰川冻土, 24(3): 219-226.

全球大幅度变暖,水循环加快,增强降水和蒸发.中国西北部从19世纪小冰期结束以来100a左右处于波动性变暖变干过程中.1987年起新疆以天山西部为主地区,出现了气候转向暖湿的强劲信号,降水量、冰川消融量和径流量连续多年增加,导致湖泊水位显著上升、洪水灾害猛烈增加、植被改善、沙尘暴减少.新疆其他地区以及祁连山中西段的降水和径流也有增加趋势.这样气候转型前景如何,是仅为年代际波动还是可发展为世纪性趋势,是只限于天山西部还是可能扩及整个西北以至华北.从引用现有区域气候模式预测,对径流变化模式预测和相似古气候情景的讨论,认为转向暖湿的趋势可以肯定,但目前尚不能确切预测转型扩大在时间上与空间上变化的速度和程度.

[4]

孙从建, 陈伟, 王诗语,

2022.

气候变化下的塔里木盆地西南部内陆河流域径流组分特征分析

[J]. 干旱区研究, 39(1): 113-122.

气候变化对中亚高山区水循环影响显著,加剧了区域水资源供需矛盾。认识区域内陆河径流组分特征对于水资源管理具有重要意义。基于塔里木盆地西南部提孜那甫河流域过去60 a（1957—2016年）的气象、径流数据,分析了区域气候变化特征及径流组分的响应。结果表明：（1）过去60 a来,流域气温及山区降水呈现出明显的上升趋势,自2010年以来区域增温增湿趋势更为明显,这一变化下提孜纳甫河夏、秋季径流呈现显著增长。（2）径流分割结果显示：冰雪融水、地下水及降水对于年径流的贡献率分别为17%,40%及43%;不同的季节的径流组分差异明显,降水对流域夏季径流的贡献较为显著。作为塔里木盆地西南部典型的内陆河流,未来区域气候变化尤其是降水的变化将会对于提孜纳甫河水资源的可持续利用影响显著。

[5]

谭剑波, 李爱农, 雷光斌,

2016.

青藏高原东南缘气象要素Anusplin和Cokriging空间插值对比分析

[J]. 高原气象, 35(4): 875-886.

选取地形起伏度巨大的青藏高原东南缘为研究区，利用该研究区96个气象站点，结合高程数据，分别采用Cokriging和Anusplin空间插值方法，获取2010年250 m分辨率的年均温度和年累计降水插值曲面。并采用交叉验证方法对比Anusplin与Cokriging插值精度，分析了误差的空间分布特征，重点对比两种插值曲面差异较大的区域精度优劣，评价两种方法在复杂地区的适用性。结果表明，Anusplin在复杂地表的插值表现优于Cokriging，其中Anusplin气温插值的均方差仅为0.82℃，而Cokriging的均方差为1.45℃；两者的降水插值精度基本一致，但Anusplin在气象要素空间异质性大的区域优于Cokriging。因此，与Cokriging相比，Anusplin更适合青藏高原东南缘复杂地表气象要素空间插值。

[6]

王海彬, 刘家宏, 刘希胜, 等,

2024.

基于ANUSPLIN插值法的青海湖流域数字流域模型研究

[J]. 水资源保护, 40(4): 82-91.

[7]

王宗太,

1991.

天山中段及祁连山东段小冰期以来的冰川及环境

[J]. 地理学报, 46(2): 160-168.

本文通过考察、航片判读、及AAR法测算了冰川变化,用地衣、文史资料、及树轮年表进行了小冰期的测年,使用实测资料分析、冰岩芯及树轮资料等估算了小冰期的气温与降水、并进而计算了地表径流的变化。在全部讨论中,还引用了一些试验性的方法和公式。

[8]

徐栋, 孔莹, 王澄海,

2016.

西北干旱区水汽收支变化及其与降水的关系

[J]. 干旱气象, 34(3): 431-439.

利用NCEP资料计算并分析1961—2010年西北干旱区（35°N—50°N，73°E—105°E）经纬向水汽输送、蒸发和水汽辐合辐散的变化特征，以及它们与同期西北干旱区降水之间的关系。结果显示：（1）西北干旱区冬、春、秋季经向水汽输送为净输入，纬向为净输出，总水汽输送为净输入。夏季经、纬向水汽输送均为净输出；（2）1961—2010年，西北干旱区各季节降水均增加，冬、春季降水增加显著，夏、秋季降水增加不显著。冬季纬向水汽净输出减少，导致西北干旱区冬季总水汽输送增加；春、秋季经向净输入减少和夏季经向净输出增加，导致春、夏、秋季总水汽输送减少；（3）1961—2010年，西北干旱区各季节蒸发量显著增加，且夏季增加趋势最显著；（4）各季节水汽通量散度显著减小，水汽辐合加强，且夏季水汽辐合增强最明显；（5）蒸发增大和水汽辐合增强是西北干旱区降水增加的主要原因，但外部水汽输送变化也会影响降水变化。

[9]

臧传富, 刘俊国,

2013.

黑河流域蓝绿水在典型年份的时空差异特征

[J]. 北京林业大学学报, 35(3): 1-10.

[10]

张乐,

2017. 渭北旱塬地区干旱—农业匹配特征研究[D]. 杨凌: 西北农林科技大学.

[11]

张强, 朱飙, 杨金虎, 等,

2021.

西北地区气候湿化趋势的新特征

[J]. 科学通报, 66(增刊2): 3 757-3 771.

[12]

张文奇, 赵媛媛, 赖宗锐, 等,

2024.

基于ANUSPLIN模型的柴达木盆地2000—2019年降水时空格局

[J]. 高原气象, 43(3): 737-748.

柴达木盆地既是响应青藏高原气候暖湿化的敏感区，又是生态环境脆弱带，评估该区域降水时空格局对水资源合理利用以及生态环境治理至关重要，然而盆地内部气象台站稀少且分布不均，为区域降水插值带来挑战。本文使用专业气象插值软件ANUSPLIN（Australian National University Spline）模型进行插值，以柴达木盆地及其周边气象台站2019年降水数据为基础，参与插值的气象台站数和9种薄盘光滑样条函数（独立变量、协变量和样条次数多种组合）为第三变量，筛选最优插值台站数和最优模型，并分析该区域2000 -2019年降水时空格局。结果表明：（1）选择盆地内部及其周边共120个气象台站，三变量局部薄盘光滑样条函数（TVPTPS4）进行区域尺度降水插值精度最高，均方根误差（RTGCV）、期望真实均方误差（RTMSE）和信噪比（SNR）均达到最小值，分别小于0.6 mm、 0.3 mm和0.25。（2）柴达木盆地降水量具有地域分布差异和季节性特征。年、季降水量东丰西少，具有明显的经向地带性特征；四季中夏季降水量最大，占全年总量的62.13%。（3）2000 -2019年，柴达木盆地年均、季节平均降水量均呈上升趋势，其中夏季降水量显著增加，最大增速达5.85 mm·a-1（p<0.05），显著增加区域约占盆地总面积的42.36%。本研究结果证明AUNSPLIN模型结果能更清晰地表达出柴达木盆地降水的分布状况，对于该区域水资源优化配置和管理等具有重要的理论和现实意义。

[13]

朱明飞, 刘海隆,

2018.

基于SWAT模型干旱区内陆河流域径流成分的模拟分析:以玛纳斯河上游为例

[J]. 石河子大学学报:自然科学版, 36(1): 89-94.

[14]

卓静, 朱延年,

2017.

秦岭主脊区年降水量空间插值最优方法研究

[J]. 干旱区地理, 40(3): 555-563.

[15]

HUTCHINSON

M F

1998.

Interpolation of rainfall data with thin plate smoothing splines-part I: Two dimensional smoothing of data with short range correlation

[J]. Journal of Geographic Information and Decision Analysis, 2(2): 152-167.

[16]

HUTCHINSON

M F

2007. ANUSPLIN Version 4.37 User Guide[M]. Canberra: The Australian National University, Centre for Resource and Environment Studies: 1-12.

[本文引用: 2]

[17]

HUTCHINSON

M F

, GESSLER

P E

1994.

Splines—more than just a smooth interpolator

[J]. Geoderma, 62(1/2/3): 45-67.

DOI URL [本文引用: 1]

[18]

HUTCHINSON

M F

1991. The application of thin plate smoothing splines to continent-wide data assimilation[M]// JASPER J D. Data Assimilation Systems. Melbourne: Bureau of Meteorology: 104-113.

[19]

KRIGE

D G

1951.

A statistical approach to some basic mine valuation problems on the witwatersrand

[J]. Journal of the Chemical, Metallurgical and Mining Society of South Africa, 52(6): 119-139.

[20]

MACDONALD

, MCKENNEY

D W

, PEDLAR

, et al,

2024.

Spatial datasets of 30-year (1991-2020) average monthly total precipitation and minimum/maximum temperature for Canada and the United States

[J]. Data in Brief, 55: 110561. DOI: 10.1016/j.dib.2024.110561.

URL [本文引用: 1]

[21]

MACDONALD

, MCKENNEY

D W

, WANG

X L

, et al,

2021.

Spatial models of adjusted precipitation for Canada at varying time scales

[J]. Journal of Applied Meteorology and Climatology, 60(3): 291-304.

DOI URL [本文引用: 1]

This study presents spatial models (i.e., thin-plate spatially continuous spline surfaces) of adjusted precipitation for Canada at daily, pentad (5 day), and monthly time scales from 1900 to 2015. The input data include manual observations from 3346 stations that were adjusted previously to correct for snow water equivalent (SWE) conversion and various gauge-related issues. In addition to the 42 331 models for daily total precipitation and 1392 monthly total precipitation models, 8395 pentad models were developed for the first time, depicting mean precipitation for 73 pentads annually. For much of Canada, mapped precipitation values from this study were higher than those from the corresponding unadjusted models (i.e., models fitted to the unadjusted data), reflecting predominantly the effects of the adjustments to the input data. Error estimates compared favorably to the corresponding unadjusted models. For example, root generalized cross-validation (GCV) estimate (a measure of predictive error) at the daily time scale was 3.6 mm on average for the 1960–2003 period as compared with 3.7 mm for the unadjusted models over the same period. There was a dry bias in the predictions relative to recorded values of between 1% and 6.7% of the average precipitations amounts for all time scales. Mean absolute predictive errors of the daily, pentad, and monthly models were 2.5 mm (52.7%), 0.9 mm (37.4%), and 11.2 mm (19.3%), respectively. In general, the model skill was closely tied to the density of the station network. The current adjusted models are available in grid form at ~2–10-km resolutions.

[22]

SHEPARD

1968.

A two-dimensional interpolation function for irregularly-spaced data

[C]// Rosenberg M. Proceedings of the 1968 23rd ACM National Conference. New York: Association for Computing Machinery: 517-524.

[23]

THIESSEN

A H

1911.

Precipitation averages for large areas

[J]. Monthly Weather Review, 39(7): 1 082-1 089.