基于空间结构函数的地面气象观测站网布局研究

doi:10.11755/j.issn.1006-7639-2025-02-0329

基于空间结构函数的地面气象观测站网布局研究

张玉洁^,¹^,²^,³

1.山东省气象工程技术中心，山东济南 250031

2.山东省气象防灾减灾重点实验室，山东济南 250031

3.长岛国家气候观象台，山东长岛 265800

Research on layout of surface meteorological observation stations based on spatial structure function

ZHANG Yujie^,¹^,²^,³

1. Shandong Meteorological Engineering Technology Center， Jinan 250031， China

2. Key Laboratory for Meteorological Disaster Prevention and Mitigation of Shandong， Jinan 250031， China

3. Changdao National Climatology Observatory， Changdao 265800， Shandong， China

责任编辑: 邓祖琴；校对：王涓力

收稿日期: 2024-04-13 修回日期: 2024-11-28

基金资助:

山东省气象局榜单类专项项目(2023SDBD08)
山东省气象局引导类科研项目(2021SDYD11)

Received: 2024-04-13 Revised: 2024-11-28

作者简介 About authors

张玉洁（1972—），女，山东烟台人，正高级工程师，主要从事探测资料应用研究。E-mail:yjzhyw@163.com。

摘要

为提高地面气象观测站网布局的科学合理性，利用1992—2021年国家级基准、基本及常规气象站观测资料，分析山东省平原和山地丘陵两类地形的气温、相对湿度、降水、气压（简称“4要素”）结构函数，确定4要素站网的最佳布站方案与布设距离，并评估现有观测站网布局的适宜性。结果表明，山地丘陵地区4要素的结构函数值均高于平原地区，平原地区结构函数更接近线性；山地丘陵在3种内插方式下的内插标准误差均高于平原地区；当距离满足点值内插标准误差小于观测标准误差时，4要素均以正三角形布站的内插精度最高。山东省国家级基准、基本及常规气象观测站的合理布站方式为正三角形布设；平原和山地丘陵的最佳布站距离分别不超过36.4、29.4 km。分要素看，气温分别不超过36.4 km和29.4 km；相对湿度不超过90.9 km和73.3 km；降水不超过81.9 km和52.3 km；气压不超过44.8 km和31.2 km。平原地区观测站网布局的适宜性优于山地丘陵地区。

关键词： 结构函数; 站网布局; 内插标准误差; 内插精度; 最大容许误差; 最大容许距离

Abstract

To enhance the scientific rationality of surface meteorological observation station network layout, this study analyzed the structural functions of air temperature, relative humidity, precipitation, and air pressure (collectively referred to as “the four elements”) in plain and hilly areas of Shandong Province using data from national reference, basic, and conventional meteorological observation stations from 1992 to 2021. The optimal station distribution scheme and spacing for the four elements were determined, and the suitability of the existing observation network was evaluated. The results show that the structural function values of the four elements are higher in hilly areas than those in plains, with structural functions in plains exhibiting a more linear pattern. The interpolation standard error under three interpolation methods is also higher in hilly areas. When the point-value interpolation standard error is smaller than the observation standard error, the highest interpolation accuracy for all four elements is achieved using an equilateral triangle station layout. In Shandong Province, the optimal layout for national reference, basic, and conventional meteorological observation stations is an equilateral triangle configuration. The optimal station spacing is no more than 36.4 km in plains and 29.4 km in hilly areas. Specifically, the optimal spacing is 36.4 km (plains) and 29.4 km (hilly areas) for air temperature; 90.9 km (plains) and 73.3 km (hilly areas) for relative humidity; 81.9 km (plains) and 52.3 km (hilly areas) for precipitation; and 44.8 km (plains) and 31.2 km (hilly areas) for air pressure. Overall, the suitability of the observation network layout is better in plain areas than in hilly areas.

Keywords： structure function; station network layout; interpolation standard error; interpolation accuracy; maximum allowable error; maximum allowable distance

PDF (2289KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张玉洁. 基于空间结构函数的地面气象观测站网布局研究[J]. 干旱气象, 2025, 43(2): 329-336 DOI:10.11755/j.issn.1006-7639-2025-02-0329

ZHANG Yujie. Research on layout of surface meteorological observation stations based on spatial structure function[J]. Arid Meteorology, 2025, 43(2): 329-336 DOI:10.11755/j.issn.1006-7639-2025-02-0329

0 引言

气象观测资料是开展天气预报预警、气候预测、气象服务和科学研究的基础（Ingleby and Lorenc，1993；Schindelegger and Ray，2014；Houchi et al.，2015；高娜等，2021；杨丽杰等，2022；杨艳玲等，2022），其中地面气象观测资料尤为重要。相比其他观测资料，地面气象观测资料能够更准确地反映近地面大气特征（Zhao et al.，2015；吕纯月等，2023）。我国对地面气象要素有着长期观测历史（王佐鹏，2020），资料主要来源于地面气象观测站，能够对气象要素进行定点、定时和高频次观测（黄晓龙等，2023）。布局合理的地面气象观测站网不仅可保障区域内任何地点观测值的内插精度，还可避免因站网过密导致的资源浪费。目前，我国国家级自动气象站多按行政区划进行布设，部分地区存在站点布局过密或过稀问题，合理性亟待提升。考虑到各省地理位置、地形地貌差异明显，因地制宜优化站网布局尤为重要。

站网布局设计最早起源于苏联，Drozdov和Shepelevskij（1946）提出气象要素内插标准误差仅与结构函数有关，结构函数由此被引入观测站网布局研究；Mooley和Ismail（1982）将结构函数应用于热带雨量站网设计中，建立了内插误差与距离的关系；Schneebeli和Laternser（2004）借助模糊数学与概率统计方法研究测雪站网布站间距；赵瑞霞等（2007）基于空间结构函数分析了北京站网布局，确定了北京东南部区域二类气象台站的最佳布站精度；岑思弦等（2015）利用四川省降水资料，通过旋转经验正交函数法计算了降水场的最大容许距离；2015年，WMO（World Meteorological Organization）在修订《WMO全球综合观测系统手册》（WMO，2015）时提出滚动需求评估（Rolling Review of Requirements，RRR）原则，以增强观测系统发展的科学性和针对性。RRR通过需求指标评估观测系统能力，分析观测需求与观测能力之间的差距，为观测站网优化提供依据。

尽管已有不少关于气象观测站网布局的研究，但大多未考虑地形地貌差异对布局设计的影响，相关成果亦较少。山东省地处华东沿海，地形复杂，涵盖平原、丘陵和山地等多种地貌类形，关于平原与山地丘陵地区站网布局的研究尚属空白。基于1992—2021年山东省国家级基准、基本及常规气象观测站资料，采用空间结构函数方法，结合地形特征，研究平原和山地丘陵两类地形的气温、相对湿度、降水和气压的最佳布站方式及距离。同时，依据WMO滚动需求评估原则，对现有国家级基准、基本及常规气象观测站网布站的适宜性进行评估，为山东省气象观测站网优化提供科学参考。

1 研究方法

1.1 结构函数

结构函数反映了变量在空间不同点间的离散程度，某气象要素在A、B两点间的结构函数 $b_{f} (A, B)$ 为该要素在两点距平差值平方的平均值（WMO，1970），计算公式如下：

（1）

b_{f} (A, B) = \bar{[∆ f (A) - ∆ f {(B)]}^{2}}

式中： $∆ f (A)$ 、 $∆ f (B)$ 分别表示气象要素f在A、B两点的距平值。用 $L$ 表示两点间距离， $L$ 可由经纬度和地球半径计算得到，计算公式如下：

（2）

L = R [2 - 2 s i n \emptyset_{A} \cdot s i n \emptyset_{B} - 2 c o s \emptyset_{A} \cdot c o s \emptyset_{B} \cdot c o s {(λ}_{A} - λ_{B} {)]}^{\frac{1}{2}}

式中： $R$ 为地球半径，单位：km； $\emptyset$ 、 $λ$ 分别为站点纬度和经度。

1.2 观测随机误差及内插标准误差

1.2.1 观测随机误差

气象要素的观测误差包括系统误差和随机误差两部分（于杰等，2003）。在计算结构函数时，系统误差已通过偏差处理消除，仅剩随机误差（范海娟，2013）。假设区域内气象要素的随机误差在各测点相互独立且方差相等，则

（3）

B_{f} (L) = b_{f} (L) + 2 σ_{f}^{2}

式中： $B_{f} (L)$ 、 $b_{f} (L)$ 分别为实际与理论结构函数， $σ_{f}^{2}$ 为观测随机标准误差。由式（3）可知，实际观测得到的结构函数高于理论值。当A、B两点重合（ $L$ =0）时， $b_{f} (0)$ =0，此时，

（4）

σ_{f}^{2} = \frac{1}{2} B_{f} (0)

将实际观测结构函数外推至零距离，可利用式（4）估算观测随机标准误差。

1.2.2 内插标准误差

讨论线段内插、正三角形内插和正方形内插3种情况。对于气象要素的插值而言，两点间中点的误差最大（王佐鹏，2020）。A、B两点间中点C的内插标准误差E计算公式（杨贤为等，1989）如下：

（5）

E = b_{f} (\frac{L}{2}) - \frac{1}{4} b_{f} (L) + \frac{1}{2} σ_{f}^{2}

在区域满足各向同性和均匀性条件下，由式（3）、（4），可得到线段内插标准误差与结构函数的关系式（杨贤为等，1989；赵瑞霞等，2007）如下：

（6）

E = B_{f} (\frac{L}{2}) - \frac{1}{4} B_{f} (L) - \frac{1}{2} B_{f} (0)

式中： $B_{f} (0)$ 为结构函数与距离关系曲线外推至零距离时的值。

对于平面正三角形和正方形中心点的内插，内插标准误差E计算公式（赵瑞霞等，2007）分别为

（7）

E = B_{f} (\frac{L}{\sqrt[]{3}}) - \frac{1}{3} B_{f} (L) - \frac{1}{2} B_{f} (0)

（8）

E = B_{f} (\frac{L}{\sqrt[]{2}}) - \frac{1}{4} B_{f} (L) - \frac{1}{8} B_{f} (\sqrt[]{2} L) - \frac{1}{2} B_{f} (0)

根据式（6）、（7）、（8），可基于各观测要素的结构函数计算不同距离下的内插标准误差E。

1.3 最大容许误差和最大容许距离

对于绝大多数气象要素，点值内插标准误差不应超过观测标准误差（WMO，1970），即最大容许误差可通过公式（5）右侧前两项的数值小于等于观测标准误差来得到（Mooley and Ismail，1982；卢文芳和王永华，1989）：

（9）

E \leq \frac{3}{2} σ_{f}^{2}

（10）即

E_{m a x} = \frac{3}{2} σ_{f}^{2} = \frac{3}{4} B_{f} (0)

因此，根据公式（10），利用站点间水平距离结构函数计算得到的最大水平容许误差E_max对应的距离即为最大水平容许距离；利用站点间垂直高度差结构函数得到的最大垂直容许误差E_max对应的距离即为最大垂直容许高度差。

1.4 观测站网水平站间距

观测站网水平站间距公式（吴薇等，2023）可表示为

（11）

C = \sqrt[]{S / (N_{1} + N_{2} + . . . + N_{m})}

（i=1，2，···，m）

式中：C为水平站间距，单位：km；S为面积，单位：km²；N_i为第i种仪器的观测站数量；m为观测要素的仪器种类数。

2 研究区及资料处理

2.1 研究区的选取

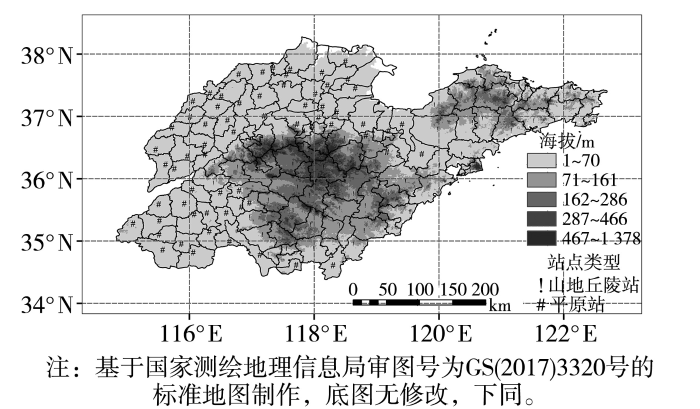
选取山东省119个国家级基准、基本及常规气象观测站，结合地形图与海拔高度，将119个站划分为64个平原站和55个山地丘陵站（图1），针对平原和山地丘陵地区的气温、相对湿度、降水和气压观测要素的站网布局进行研究。鉴于研究区域内山地和丘陵站的海拔高度差异较小，且空间分布相邻，本文将山地和丘陵合并为一类进行分析。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 山东省64个平原站和55个山地丘陵站分布

Fig.1 Distribution map of 64 plain stations and 55 mountain and hill stations in Shandong Province

相关研究（白光弼和刘岳俊，1992）表明，站网设计需同时考虑水平方向的最大容许距离和垂直方向的最大容许高度差。根据前文的计算方法，得到各要素在垂直方向的最大容许高度差，平原地区气温、相对湿度、降水和气压该值分别为102、149、156、135 m；山地丘陵地区该4要素垂直方向的最大容许高度差分别为303、369、357、326 m。在所选的64个平原站和55个山地丘陵站中，平原站的最大高度差为73 m，山地丘陵站点为300 m，均未超过相应气象要素的最大容许高度差，因此，本文研究中垂直高度差对内插标准误差的影响可忽略。

2.2 资料的选取与处理

使用山东省国家级基准、基本及常规气象观测站1992—2021年的日平均气温、相对湿度、降水量和平均气压资料。所有观测数据均经过空间一致性和时间连续性等质量控制。除降水资料外，其他要素每隔2 d选取1 d数据样本，以减弱相邻数据的过强相关性（赵瑞霞等，2007）。降水的绝对内插误差通常与降水量大小成正比，研究表明（Mooley and Ismail，1982；张强和杨贤为，1992），雨量站网设计需重点考虑降水集中的月份或季节。因此，本文选取每年4—10月的日降水数据开展雨量站网布局研究。

以平原站为例，资料处理步骤如下：

1 ）结构函数与距离的计算

根据公式（1）和公式（2），分别计算64个平原站任意两站间的结构函数与水平距离，共得到m（m-1）/2（m为站点个数64）对结构函数与距离值。参考相关研究（赵瑞霞等，2007；王佐鹏，2020），以20 km为间隔将站间距分组，计算各区间内结构函数的平均值，绘制距离与结构函数关系曲线，并将曲线外推至距离零处，以求得实际结构函数 $B_{f} (0)$ 的值。

2 ）内插标准误差计算

利用实际结构函数与距离的关系曲线拟合回归方程，代入公式（6）、（7）、（8），分别计算不同距离下线段、正三角形和正方形布设方式的内插标准误差，并绘制内插标准误差随距离变化的曲线。

3 ）最大容许误差与最大容许距离计算

将外推至距离零的结构函数代入公式（10），计算最大容许内插标准误差。结合不同布设方式下内插标准误差随距离的变化曲线，确定最大容许内插标准误差对应的距离，即为最大容许距离。

3 结果与讨论

3.1 地面气温、相对湿度、降水及气压的结构函数

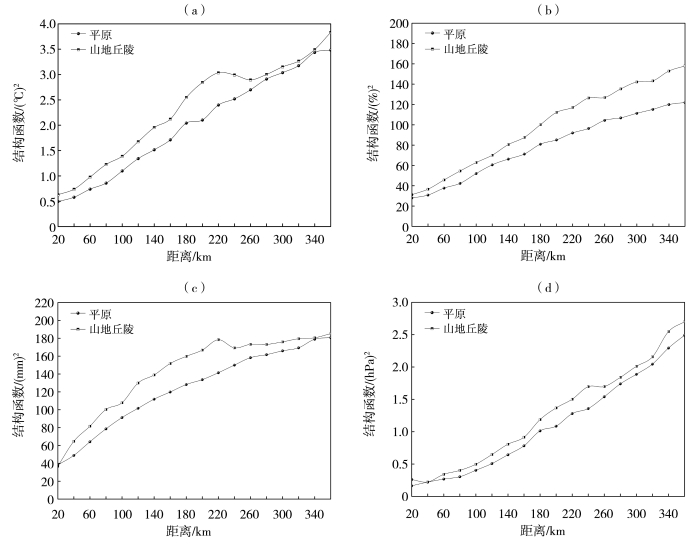
由图2可知，平原和山地丘陵两类地形下的气温、相对湿度、降水和气压的结构函数随距离的变化存在明显差异。平原地区各要素的结构函数随距离增大而平稳上升，整体变化较为平滑，接近线性；而山地丘陵地区各要素的结构函数随距离的波动幅度较大，且各要素的结构函数值普遍高于平原地区。这表明不同地形条件下观测要素的空间变异性存在差异，随着地形起伏和海拔高度的增加，各要素序列差值的离散程度加大。由于结构函数反映了气象要素在空间不同点之间的离散程度，因此山地丘陵与平原地区呈现不同的结构特征，体现了地形对要素空间变异性的影响。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 山东1992—2021年平原及山地丘陵日平均气温（a）、平均相对湿度（b）、降水量（c）及平均气压（d）的结构函数随距离的变化

Fig.2 Variation of the structural functions of daily average temperature (a), average relative humidity (b), precipitation (c) and average pressure (d) change with distance in plain and hilly areas in Shandong from 1992 to 2021

3.2 结构函数拟合

为得到气温、相对湿度、降水和气压结构函数随距离变化的回归方程，分别采用线性、二次多项式、三次多项式和指数函数进行拟合。结果表明，二次和三次多项式拟合效果较好，相关系数相近。考虑到兼顾拟合精度和模型简洁性，拟合效果差异较小时优先选用低阶多项式。各要素结构函数的拟合方程见表1。

表1 山东1992—2021年日平均气温、平均相对湿度、降水量及平均气压结构函数与距离的回归方程

Tab.1 The regression equations of the structural functions of daily average temperature， average relative humidity， precipitation and average pressure with distance in Shandong from 1992 to 2021

要素	站点类型	回归方程
气温	平原	$b'_{f} = 0.157 4 + 0.010 3 \times L - 2.454 \times 10^{- 6} \times L^{2}$
气温	山地丘陵	$b'_{f} = 0.184 6 + 0.015 1 \times L - 1.536 \times 10^{- 5} \times L^{2}$
相对湿度	平原	$b'_{f} = 15.473 2 + 0.407 1 \times L - 2.946 \times 10^{- 4} \times L^{2}$
相对湿度	山地丘陵	$b'_{f} = 16.134 1 + 0.526 4 \times L - 3.652 \times 10^{- 4} \times L^{2}$
降水	平原	$b'_{f} = 24.648 5 + 0.718 8 \times L - 8.059 \times 10^{- 4} \times L^{2}$
降水	山地丘陵	$b'_{f} = 23.237 4 + 1.063 1 \times L - 1.780 \times 10^{- 3} \times L^{2}$
气压	平原	$b'_{f} = 0.054 7 + 0.002 9 \times L + 1.073 \times 10^{- 5} \times L^{2}$
气压	山地丘陵	$b'_{f} = 0.057 8 + 0.004 4 \times L + 7.825 \times 10^{- 6} \times L^{2}$

新窗口打开| 下载CSV

3.3 内插标准误差与距离的关系

将表1中的回归方程分别代入公式（6）、（7）、（8），得到平原和山地丘陵地区气温、相对湿度、降水和气压在不同布站方式（线段、正三角形、正方形）下的内插标准误差与距离的关系式（表2）。由表2绘制的内插标准误差随距离变化的曲线（图3）显示，平原和山地丘陵各要素在3种布站方式下的内插标准误差均随距离增加而增大，且山地丘陵地区的内插标准误差普遍高于平原地区，反映出其时间变幅和空间梯度较大。

表2 山东1992—2021年3种内插方式气温、相对湿度、降水量和气压的内插标准误差与距离的关系式

Tab.2 The relationship between the interpolation standard error of temperature， relative humidity， precipitation and pressure and distance under three interpolation methods in Shandong from 1992 to 2021

要素	站点类型	内插方式	内插标准误差与距离的关系式	要素	站点类型	内插方式	内插标准误差与距离的关系式
气温	平原	线段	$E = 0.039 4 + 2.575 \times 10^{- 3} \times L$	降水	平原	线段	$E = 6.162 + 1.797 \times 10^{- 1} \times L$
		正三角形	$E = 0.026 2 + 2.513 \times 10^{- 3} \times L$			正三角形	$E = 4.108 + 1.754 \times 10^{- 1} \times L$
		正方形	$E = 0.019 7 + 2.887 \times 10^{- 3} \times L$			正方形	$E = 3.081 + 2.015 \times 10^{- 1} \times L$
	山地丘陵	线段	$E = 0.046 2 + 3.775 \times 10^{- 3} \times L$		山地丘陵	线段	$E = 5.809 + 2.658 \times 10^{- 1} \times L$
		正三角形	$E = 0.030 8 + 3.685 \times 10^{- 3} \times L$			正三角形	$E = 3.873 + 2.594 \times 10^{- 1} \times L$
		正方形	$E = 0.023 1 + 4.233 \times 10^{- 3} \times L$			正方形	$E = 2.905 + 2.980 \times 10^{- 1} \times L$
相对湿度	平原	线段	$E = 3.868 + 1.018 \times 10^{- 1} \times L$	气压	平原	线段	$E = 0.013 7 + 7.250 \times 10^{- 4} \times L$
		正三角形	$E = 2.579 + 9.934 \times 10^{- 2} \times L$			正三角形	$E = 0.009 1 + 7.076 \times 10^{- 4} \times L$
		正方形	$E = 1.934 + 1.141 \times 10^{- 1} \times L$			正方形	$E = 0.006 8 + 8.130 \times 10^{- 4} \times L$
	山地丘陵	线段	$E = 4.034 + 1.316 \times 10^{- 1} \times L$		山地丘陵	线段	$E = 0.014 5 + 1.10 \times 10^{- 3} \times L$
		正三角形	$E = 2.689 + 1.285 \times 10^{- 1} \times L$			正三角形	$E = 0.009 6 + 1.074 \times 10^{- 3} \times L$
		正方形	$E = 2.017 + 1.476 \times 10^{- 1} \times L$			正方形	$E = 0.007 2 + 1.233 \times 10^{- 3} \times L$

新窗口打开| 下载CSV

进一步分析表2和图3可见，距离较小时，正方形布站内插精度最高，线段内插精度最低；当距离超过某一临界值后，正三角形布站的内插精度最高，正方形最低。该临界值随气象要素种类而异。距离相同时，降水的内插标准误差最大，与其结构函数值最大的特征相一致。这主要由于降水在时间和空间上的分布极不均匀，变化幅度大，从而导致内插标准误差明显高于其他要素。

图3

新窗口打开| 下载原图ZIP| 生成PPT

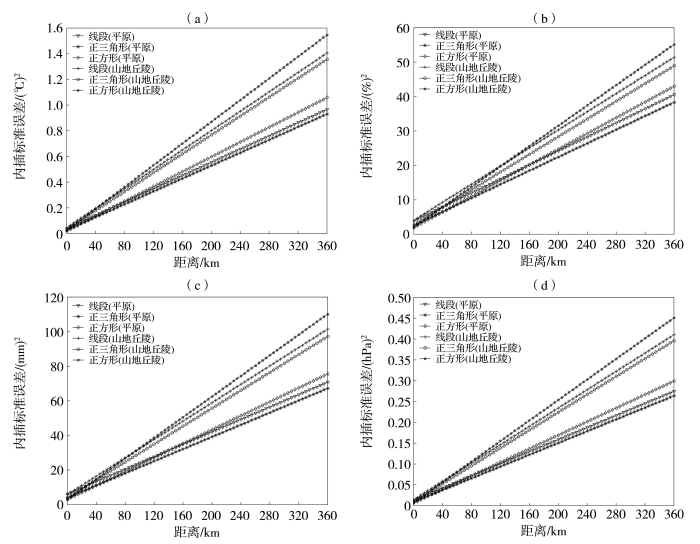
图3 山东1992—2021年平原和山地丘陵气温（a）、相对湿度（b）、降水量（c）和气压（d）在3种内插方式下的内插标准误差随距离的变化

Fig.3 The changes of interpolation standard errors of temperature (a), relative humidity (b), precipitation (c) and air pressure (d) with distance in plains and hilly areas in Shandong from 1992 to 2021 under three interpolation methods

3.4 最大容许内插标准误差与最大容许距离

表3为气温、相对湿度、降水和气压在线段、正三角形和正方形3种内插方式下的最大容许距离。由表可见，对于平原地区，气温、相对湿度和气压的最大容许内插误差均小于山地丘陵，且在3种内插方式下的最大容许距离均大于山地丘陵；而降水的最大容许内插误差在平原地区高于山地丘陵，对应的最大容许距离也更大。各要素的最大容许内插距离由最大容许误差和内插精度共同决定，受要素的时间变化幅度、空间梯度及观测随机标准误差等因素影响。山地丘陵地区受复杂地形和局地气候影响，各要素时间变化幅度和空间梯度普遍大于平原地区，且图3显示山地丘陵地区内插精度低于平原地区，这些差异共同导致两类地形间最大容许内插距离的差异。

表3 各观测要素在3种布站方案下的最大容许内插标准误差和最大容许距离

Tab.3 Maximum allowable interpolation standard error and maximum allowable distance of each observation element under three stationing schemes

要素	区域	E_max	$\sqrt[]{E_{m a x}}$	最大容许距离/km
要素	区域	E_max	$\sqrt[]{E_{m a x}}$	线段内插	正三角形内插	正方形内插
气温	平原	0.118/（℃）²	0.344/℃	30.4	36.4	33.9
气温	山地丘陵	0.138/（℃）²	0.371/℃	24.6	29.4	27.4
相对湿度	平原	11.605/（%）²	3.407/%	76.0	90.9	84.7
相对湿度	山地丘陵	12.101/（%）²	3.479/%	61.3	73.3	68.3
降水	平原	18.486/（mm）²	4.30/mm	68.6	81.9	76.5
降水	山地丘陵	17.428/（mm）²	4.175/mm	43.7	52.3	48.7
气压	平原	0.041/（hPa）²	0.202/hPa	37.5	44.8	41.8
气压	山地丘陵	0.043/（hPa）²	0.207/hPa	26.1	31.2	29.1

新窗口打开| 下载CSV

结合图3和表3可知，在距离满足点值内插标准误差小于观测标准误差的条件下，对于平原和山地丘陵地区气温、相对湿度、降水和气压的最佳内插方式均为正三角形布设，其最大容许距离也相对最大。因此，正三角形布设是山东省平原和山地丘陵地区气象观测站科学合理的布局方式。具体而言，平原（山地丘陵）地区的最佳布站距离为：气温36.4 km（29.4 km）、相对湿度90.9 km（73.3 km）、降水81.9 km（52.3 km）、气压44.8 km（31.2 km）。

由于山东省国家级基准、基本及常规气象观测站为多要素联合观测站，因此，其布站方案需综合考虑各要素需求。根据最小布设需求，以气温要素的最佳布站距离为控制标准，平原地区的最佳站间距不超过36.4 km，山地丘陵不超过29.4 km。

3.5 基于最佳站间距的山东省国家级基准、基本及常规气象观测站布局评估

基于观测站网水平站间距计算公式（11），计算了山东省16个地市国家级基准、基本及常规气象观测站各要素的现有水平站间距，并根据研究得到的最大容许距离估算了最佳站间距下的布设站点数（表4）。在评估过程中，将16个地市划分为平原、山地丘陵、平原与山地丘陵混合3类地形。其中，济南、济宁、临沂、泰安、潍坊、枣庄、淄博7个地市属混合地形，计算最佳站间距对应的站点需求时按各地实际地貌将总面积按平原和山地丘陵占比分别计算站点数（具体占比情况见表4的表注2）。由于缺乏山东省精细化地形数据，相关占比为估算值，且分析仅考虑平原和山地丘陵两类地貌。

表4 山东省16个地市现有国家级基准、基本及常规气象观测站站间距、站点数与最佳站间距及站点数的对比

Tab.4 Comparison of the existing station spacing and number of national reference， basic and conventional meteorological observation stations in 16 prefecture-level cities of Shandong Province with the optimal station spacing and number

地市	现有国家级基准、基本及常规气象观测站		国家级基准、基本及常规气象观测站最佳站间距及站点数
	站间距/km	站点数/个	平原		山地丘陵
	站间距/km	站点数/个	站间距/km	站点数/个	站间距/km	站点数/个
滨州	36.2	7	36.4	7
东营	40.6	5	36.4	6
菏泽	36.8	9	36.4	9
德州	30.7	11	36.4	8
聊城	32.8	8	36.4	7
济南	33.8	7	36.4	4	29.4	4
济宁	31.9	11	36.4	5	29.4	5
临沂	41.5	10	36.4	5	29.4	12
泰安	35.9	6	36.4	2	29.4	6
潍坊	42.4	9	36.4	8	29.4	7
枣庄	30.2	5	36.4	2	29.4	3
淄博	27.3	8	36.4	1	29.4	5
青岛	40.2	7			29.4	13
日照	42.3	3			29.4	6
威海	31.1	6			29.4	7
烟台	35.5	11			29.4	16

注： 1. 平原和山地丘陵站点数为四舍五入法取整；2. 混合地形面积占比（地名/平原面积占比/山地丘陵面积占比）：济南/60%/40%，济宁/65%/35%，临沂/40%/60%，泰安/40%/60%，潍坊/65%/35%，枣庄/45%/55%，淄博/28%/72%。

新窗口打开| 下载CSV

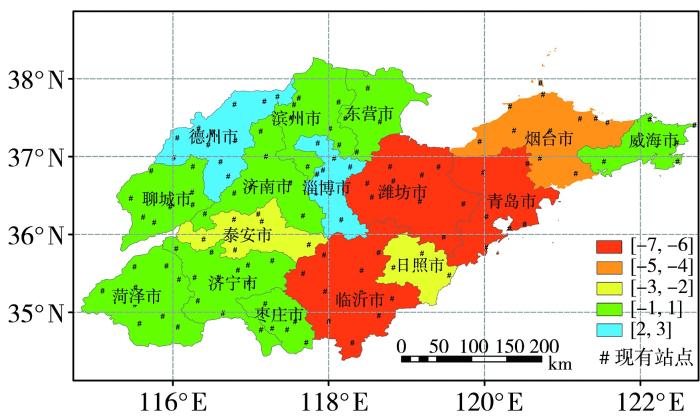
通过山东省现有国家级基准、基本及常规气象观测站的站间距和站点数量与研究所得最佳值的对比（表4、图4）可见，平原地区的5个地市中，德州和东营现有站间距与最佳站间距差异较大，其余3地接近最佳值；平原与山地丘陵混合地区的7个地市中，淄博的现有站间距小于最佳站间距，潍坊和临沂大于最佳站间距，其余4地介于二者之间；山地丘陵地区的4个地市现有站间距均大于最佳站间距，其中青岛、日照差异最明显。图4显示，鲁西北（除德州）、鲁南（除临沂、日照）、鲁中（济南）及半岛（威海）的站网布局较为合理，现有站点数与最佳站点数的差值为-1~1。临沂、潍坊、青岛、烟台4地的站点数明显不足，与最佳站点数的差值为-7~-5；泰安、日照分别少2个和3个站点，也需适当增补；德州、淄博的站点数分别超出最佳站点数3个和2个，布局稍显密集。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 山东省16个地市国家级基准、基本及常规气象观测站现有站点数与最佳站点数的差值分布

Fig.4 The difference distribution between the existing number of sites and the optimal number of sites of national reference， basic and conventional meteorological observation stations in the 16 prefecture-level cities of Shandong Province

综上，山东省国家级基准、基本及常规气象观测站的布局适宜性总体上平原地区优于山地丘陵地区。

4 结论与讨论

利用山东省1992—2021年的国家级基准、基本及常规气象观测站的资料，分析了平原与山地丘陵地区气温、相对湿度、降水、气压的结构函数及内插标准误差的变化特征，确定了最佳布站方式和布站距离，并评估了现有站网布局的适宜性，得到以下主要结论。

1 ）平原地区气温、相对湿度、降水、气压的结构函数均随距离增加而增大，函数较为平滑，接近线性；山地丘陵地区的结构函数波动幅度更明显，且在相同距离下，其结构函数值普遍高于平原地区。

2 ）采用线段、正三角形或正方形内插方式，平原和山地丘陵地区的各要素内插标准误差均随距离增加而增大，且呈线性关系。在相同距离下，山地丘陵地区的内插标准误差高于平原地区。当点值内插标准误差小于观测标准误差时，正三角形内插方式的精度最高。

3 ）山东省平原和山地丘陵地区的气温、相对湿度、降水、气压最佳的布站方式均为正三角形布设。最佳布站距离分别为：气温36.4 km（平原）、29.4 km（山地丘陵）；相对湿度90.9 km（平原）、73.3 km（山地丘陵）；降水81.9 km（平原）、52.3 km（山地丘陵）；气压44.8 km（平原）、31.2 km（山地丘陵）。降水的最佳布站距离大于气温和气压，可能与研究选取降水集中的4—10月数据，以及降水采用日降水量，而气温和气压采用日平均值有关。

4 ）山东省国家级基准、基本及常规气象观测站的合理布站方式为正三角形布设，平原地区的最佳布站距离不超过36.4 km，山地丘陵地区不超过29.4 km。现有站点布设评估结果显示，平原地区站点布局适宜性优于山地丘陵地区。

由于山东省区域气象观测站资料的时序较短，数据质控效果有待提升，本文仅基于国家级基准、基本及常规气象观测站的资料讨论了平原和山地丘陵地区主要气象要素的最佳布站方式与距离。鉴于日平均风速受站点环境影响较大，本文未对风要素进行分析，但研究方法同样适用于风场站网布局。此外，本文研究方法也可推广至其他省份的不同地形区域，用于优化各气象要素的布站方式和布站距离，对于加密布设的区域气象观测站，若数据时序较长、连续性好、质控效果佳，亦可用本研究方法优化布站方案和距离。本研究结果对自动气象观测站的站网布局优化和升级具有重要参考价值。然而，气象观测站网布局还涉及站点位置的优化及不同观测要素的合理配置等复杂问题，仍需进一步深入研究。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

白光弼, 刘岳俊,

1992.

高原和山区气象站网的合理布局

[J]. 陕西气象(3):18-21.