新疆戈壁地区风沙流结构及其粒径特征研究
1
2019
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
兰新铁路百里风区风沙流结构特性研究
1
2010
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
兰新铁路十三间房段的戈壁风沙流特征分析
1
2010
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
利用静态小波变换的非定常阵风分析与模拟
1
2009
... 图2、图4~6各时间序列对应的Hilbert边际谱见图7~10.可以看出,虽然不同序列的脉动项差异很大,但谱特征非常一致.这是因为通过定义沙尘事件剔除了时间序列中无风沙活动的影响.所有计算结果均表明,无论风、沙还是尘的各种特征量的Hilbert边际谱均随着频率升高先迅速上升后缓慢下降.这说明公式(6)和(7)的幂次标度律猜测比较合理.可能轻视风沙流的间歇性、小波基选取不当或者对极少序列的不恰当平均等原因,Baas(2006)得到的风速和输沙率密度小波谱并没有如此良好的规律性.由Karman经验谱公式能够得到很好的全局性风速能谱拟合结果(刘江和王元,2009).在壁湍流的不同频率区间内,风速能谱分别符合经典的“-1”和“-5/3”标度律(Marusic and Monty,2019).可能受沙尘运动或地形起伏影响,我们得到的能谱难以进一步按频率区间进行区分.因此,将Hilbert边际谱最大值时的频率作为幂次标度律区间起点来拟合公式(6)和(7)中的各标度指数.对于同一个沙尘事件,跃移沙粒动能和个数的标度指数可能存在较大差异(图7),也可能非常接近(图8).跃移沙粒动能和个数是相互独立的物理量,在个别事件中的标度指数接近属于巧合.人工地表和天然地表的粗糙元差别很大,前者以砾石为主,后者存在植被,从而导致二者的近地表气流场结构及相同高度处粉尘浓度标度指数均存在很大差异. ...
两种戈壁地表风沙流特征的野外观测
3
2020
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
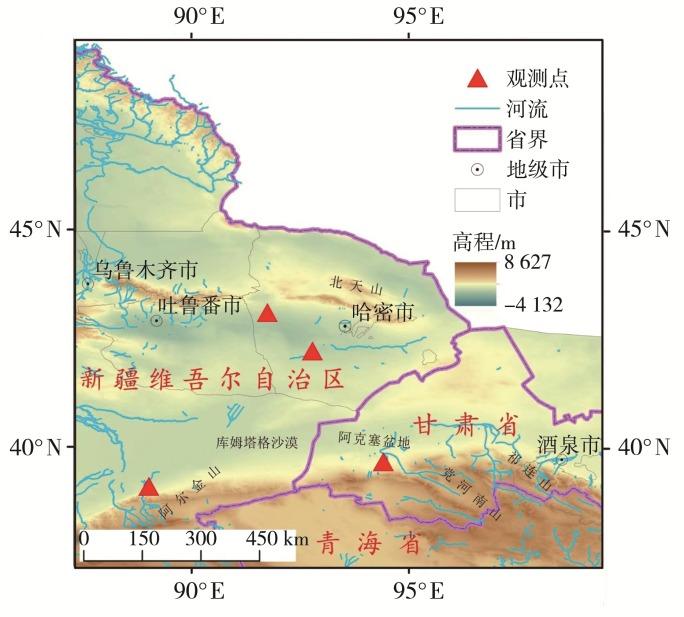
... 4 )观测地点位于党河南山以北的阿克塞盆地中(94.40°E,39.70°N),分别在去除植被并对上风向地表实施化学固沙措施的人工观测场和约15%植被盖度的自然观测场中进行观测,所测量的PM10质量浓度分别称为人工地表和天然地表粉尘浓度.两个观测场地表物质均以粗砂和中砂为主,质量比83%~91%.受地形影响,观测地点处于低风能环境中.对观测场的具体描述见相关文献(刘旭阳等,2020;Zhang et al.,2022).该数据集包括14 d人工观测场和5 d自然观测场内5个高度处的PM10质量浓度和2个高度处的3个风速分量,由本研究团队于2017年3月16日—5月2日期间陆续观测获得. ...
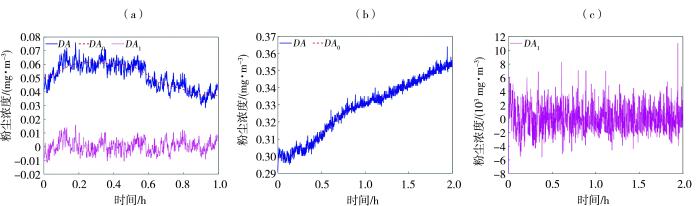
... 0.10 m高度处两组粉尘浓度时间序列的分解结果见图5,模态项数均为6.其中,人工地表粉尘浓度专指在去除植被且对上风向边界处地表做过不可蚀处理的观测场(刘旭阳等,2020;Zhang et al.,2022)内测量的粉尘浓度.因为并非同步观测,图5中人工和天然戈壁观测场的粉尘浓度不具有可比性.在1 h内,人工观测场近地表粉尘浓度大致表现为先增加后稳定再下降的趋势,因趋势项数值较低,脉动现象比较明显;天然观测场的沙尘浓度一直呈缓慢上升趋势,因为趋势项数值较大,脉动项更像在零点附近波动的噪声,实际并非如此,脉动项振幅与人工观测场很接近,亦有一定的动态规律性. ...
莫高窟顶戈壁偏东风作用下输沙率变化的观测研究
1
2010
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
戈壁风沙流结构特性及其意义
1
2005
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
几种典型戈壁床面风沙流特性比较
1
2012
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
1
2008
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
金阿铁路戈壁风沙流输沙量研究
1
2019
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
戈壁地表风沙运动特征的野外观测研究
1
2010
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
砾漠大风地区风沙流及铁路防沙技术研究
1
1990
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
戈壁风沙流结构和风速廓线特征研究
1
2005
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
人工模拟戈壁风沙流与风程效应观测
1
2011
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
戈壁风沙流若干特征研究
1
1995
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
Wavelet power spectra of aeolian sand transport by boundary layer turbulence
2
2006
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
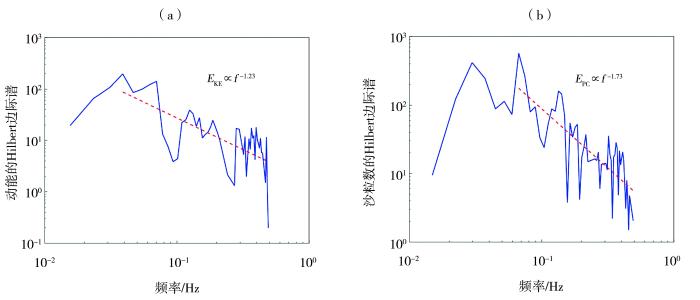
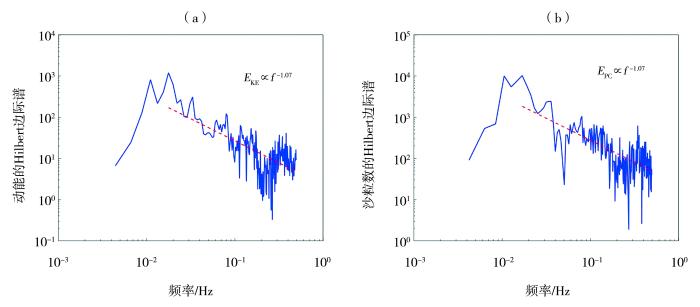
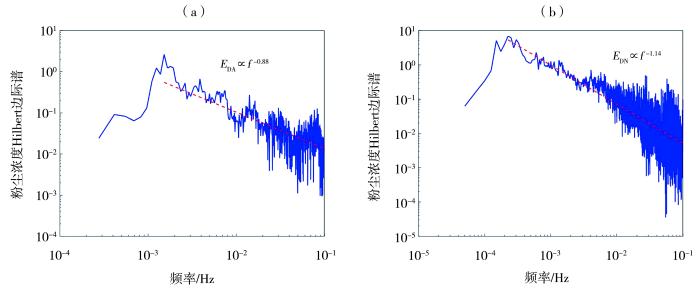
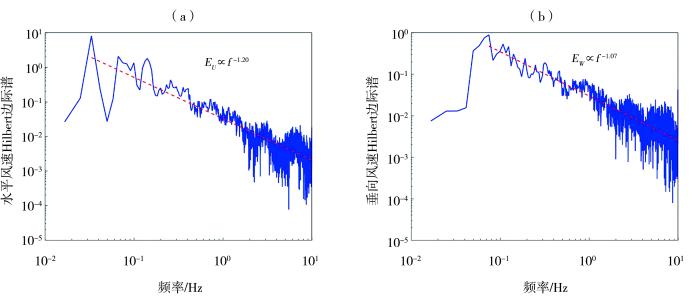
... 图2、图4~6各时间序列对应的Hilbert边际谱见图7~10.可以看出,虽然不同序列的脉动项差异很大,但谱特征非常一致.这是因为通过定义沙尘事件剔除了时间序列中无风沙活动的影响.所有计算结果均表明,无论风、沙还是尘的各种特征量的Hilbert边际谱均随着频率升高先迅速上升后缓慢下降.这说明公式(6)和(7)的幂次标度律猜测比较合理.可能轻视风沙流的间歇性、小波基选取不当或者对极少序列的不恰当平均等原因,Baas(2006)得到的风速和输沙率密度小波谱并没有如此良好的规律性.由Karman经验谱公式能够得到很好的全局性风速能谱拟合结果(刘江和王元,2009).在壁湍流的不同频率区间内,风速能谱分别符合经典的“-1”和“-5/3”标度律(Marusic and Monty,2019).可能受沙尘运动或地形起伏影响,我们得到的能谱难以进一步按频率区间进行区分.因此,将Hilbert边际谱最大值时的频率作为幂次标度律区间起点来拟合公式(6)和(7)中的各标度指数.对于同一个沙尘事件,跃移沙粒动能和个数的标度指数可能存在较大差异(图7),也可能非常接近(图8).跃移沙粒动能和个数是相互独立的物理量,在个别事件中的标度指数接近属于巧合.人工地表和天然地表的粗糙元差别很大,前者以砾石为主,后者存在植被,从而导致二者的近地表气流场结构及相同高度处粉尘浓度标度指数均存在很大差异. ...
Challenges in aeolian geomorphology: Investigating aeolian streamers
1
2008
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
Transitional behaviour of saltation: Wind tunnel observations of unsteady winds
1
1998
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
Fundamental causes of model inaccuracies in predicting wind-blown sand fluxes
1
2023
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
Characteristics of the disastrous wind-sand environment along railways in the Gobi area of Xinjiang, China
2
2015
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
... 1 )观测地点位于吐鲁番—哈密盆地中部十三间房的天山冲洪积扇上(91.73°E,43.13°N),鹅卵石覆盖度高达87%左右,年平均风速7.13 m·s-1,最大瞬时风速56.60 m·s-1,年均大风(10 m高度处风速超过17.10 m·s-1)日数179 d(Cheng et al.,2015),处于高风能环境中.仪器布设详见Wang等(2022)文献,观测的物理量包括气温、气压、空气湿度、风速、输沙率等.本文仅分析一个由862 000条风速记录组成的子数据集. ...
Improved complete ensemble EMD: A suitable tool for biomedical signal processing
2
2014
... 式中:t为时间, 为趋势项, 为总脉动项, 为有限阶脉动项,m为项数.每个脉动项又称模态,必须满足极值点与过零点个数最多相差一个且上下包络之和处处为零两个条件.最初的经验模态分解算法存在分解不彻底与模态混杂问题(Huang et al.,1998;de Souza et al.,2022).通过在每个分解步骤中添加自适应白噪声信号,可以保证模态之间的正交性(Colominas et al.,2014). ...
... 具体计算时,首先按Colominas等(2014)改进的自适应噪声完备集合经验模态分解(Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, ICEEMDAN)算法实现公式(1)形式的正交分解,然后根据公式(2)~(5)得到Hilbert边际谱,最后探讨各Hilbert边际谱是否符合公式(6)和(7)的形式,若符合则利用最小二乘法拟合得到各指数值. ...
High-frequency sediment transport responses on a vegetated foredune
2
2012
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... )、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
A survey on Hilbert-Huang transform: Evolution, challenges and solutions
4
2022
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... 式中:t为时间, 为趋势项, 为总脉动项, 为有限阶脉动项,m为项数.每个脉动项又称模态,必须满足极值点与过零点个数最多相差一个且上下包络之和处处为零两个条件.最初的经验模态分解算法存在分解不彻底与模态混杂问题(Huang et al.,1998;de Souza et al.,2022).通过在每个分解步骤中添加自适应白噪声信号,可以保证模态之间的正交性(Colominas et al.,2014). ...
... 式中:t1和t2分别为沙尘事件的起止时刻,时长T=t2-t1.Hilbert边际谱 表征特征频率为f的脉动风速的能量密度,是传统Fourier谱的一种替代,二者总体特征类似,但局部细节有所区别(de Souza et al.,2022).同样地,可以得到垂向风速W、跃移沙粒动能KE和个数PC、粉尘浓度DA和DN的Hilbert边际谱. ...
... 按照沙尘事件定义和时间序列选取方法,从4个数据集中筛选出1~37个时长不等的沙尘事件,并依次选取1 724、1 006、98和486个风速序列.实际计算表明,脉动项个数m一般为4~10.每个风速脉动项具有不同的特征时间尺度,彼此叠加即可构成复杂的湍流相干结构.除了地表影响,沙尘脉动主要由风速脉动引起.如果表征风与沙的脉动项之间的小波相干系数较大,那么二者之间大致成正比例关系(Wang et al.,2018).每个脉动项都有自己的特征频率,可通过构造复频率方式定量描述风与沙脉动项之间的相互作用(Wang,2024).不同于小波变换,Hilbert-Huang变换尚缺乏严格的数学基础(de Souza et al.,2022).这里仅将模态分解算法作为计算Hilbert谱的一种有效手段. ...
Cross-wavelet analysis of coherent wind and saltation events
1
2023
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis
1
1971
... 式中:t为时间, 为趋势项, 为总脉动项, 为有限阶脉动项,m为项数.每个脉动项又称模态,必须满足极值点与过零点个数最多相差一个且上下包络之和处处为零两个条件.最初的经验模态分解算法存在分解不彻底与模态混杂问题(Huang et al.,1998;de Souza et al.,2022).通过在每个分解步骤中添加自适应白噪声信号,可以保证模态之间的正交性(Colominas et al.,2014). ...
A review on Hilbert-Huang transform: Method and its applications to geophysical studies
1
2008
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
Large scale sand saltation over hard surface: A controlled experiment in still air
1
2021
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
Wind speed characteristics and blown sand flux over a gravel surface in a compact wind tunnel
1
2018
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
Attached eddy model of wall turbulence
1
2019
... 图2、图4~6各时间序列对应的Hilbert边际谱见图7~10.可以看出,虽然不同序列的脉动项差异很大,但谱特征非常一致.这是因为通过定义沙尘事件剔除了时间序列中无风沙活动的影响.所有计算结果均表明,无论风、沙还是尘的各种特征量的Hilbert边际谱均随着频率升高先迅速上升后缓慢下降.这说明公式(6)和(7)的幂次标度律猜测比较合理.可能轻视风沙流的间歇性、小波基选取不当或者对极少序列的不恰当平均等原因,Baas(2006)得到的风速和输沙率密度小波谱并没有如此良好的规律性.由Karman经验谱公式能够得到很好的全局性风速能谱拟合结果(刘江和王元,2009).在壁湍流的不同频率区间内,风速能谱分别符合经典的“-1”和“-5/3”标度律(Marusic and Monty,2019).可能受沙尘运动或地形起伏影响,我们得到的能谱难以进一步按频率区间进行区分.因此,将Hilbert边际谱最大值时的频率作为幂次标度律区间起点来拟合公式(6)和(7)中的各标度指数.对于同一个沙尘事件,跃移沙粒动能和个数的标度指数可能存在较大差异(图7),也可能非常接近(图8).跃移沙粒动能和个数是相互独立的物理量,在个别事件中的标度指数接近属于巧合.人工地表和天然地表的粗糙元差别很大,前者以砾石为主,后者存在植被,从而导致二者的近地表气流场结构及相同高度处粉尘浓度标度指数均存在很大差异. ...
Intermittent aeolian saltation: A protocol for quantification
2
2018
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... )等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
Influence of sand transport rate on rolling wear and damage behaviors of wheel/rail in Gobi and desert windblown sand environments
1
2022
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
One-dimensional transitional behaviour in saltation
1
2000
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
Intermittent saltation
2
1997
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... ).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
Intermittent aeolian saltation over a gobi surface: Threshold, saltation layer height, and high-frequency variability
9
2020
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... Datasets of aeolian sand and dust motions over Gobi and measurement conditions
Tab.1 | 数据来源 | 高度/m | 物理量 | 传感器(厂家) | 采样频率/Hz | 采样精度 |
| Wang et al.,2022 | 0.30、0.83、3.00 | U、V、W | WindMaster Pro(Gill) | 20 | 0.001 m·s-1 |
| Tan et al.,2020 | 0.05、0.12、0.38、0.80、1.38 | KE、PC | H11-Lin(Sensit) | 1 | 1×10-7 J·s-1、s-1 |
| 0.70、2.00 | U、φ、θ | Young-81000(RM Young) | 20 | 0.01 m·s-1、0.1° |
| Wang et al.,2023 | 0.05、0.12、0.38、0.80、1.41 | KE、PC | H11-Lin(Sensit) | 1 | 1×10-7 J·s-1、s-1 |
| 1.20、2.80 | U、V、W | WindMaster Pro(Gill) | 1 | 0.001 m·s-1 |
| 本研究团队 | 0.10、0.20、0.50、1.00、1.50、2.00 | DA、DN | DustTrak-II(TSI) | 0.2 | 0.001 mg·m-3 |
| 0.50、1.00 | U、V、W | Young-81000(RM Young) | 20 | 0.01 m·s-1 |
注:U为球坐标系下的风速大小或直角坐标系下的水平风速分量;V为直角坐标系下的另一个水平风速分量;W为垂向风速;φ为仰角,θ为方位角;KE为动能,PC为个数;DA为人工地表粉尘浓度,DN为天然地表粉尘浓度.下同. ...
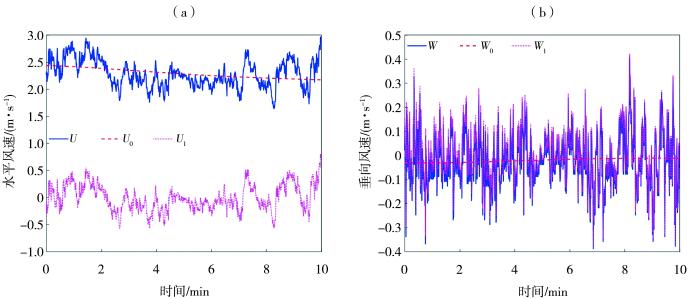
... 2 )观测地点位于阿尔金山西麓新疆若羌县米兰镇的阿尔金山冲洪积扇上(89.00°E,39.13°N),40%~50%的地表被细小砾石覆盖,年均大风日数为13 d,处于高风能环境中.仪器布设详见Tan等(2020)文献.该数据集共有25 200条跃移沙粒记录和504 000条风速记录,每条记录包含5个高度处的沙粒动能和个数与2个高度处的风速、仰角和方位角,详细描述及下载链接见Mendeley网站(https://doi.org/10.17632/jdjmg8s544.1). ...
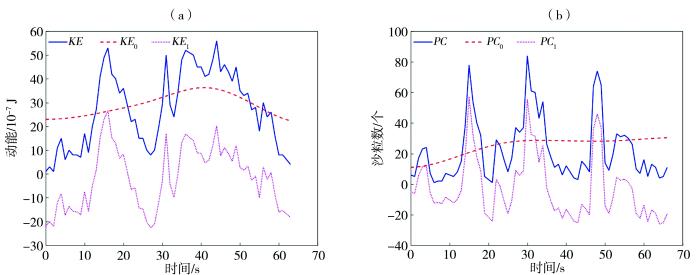
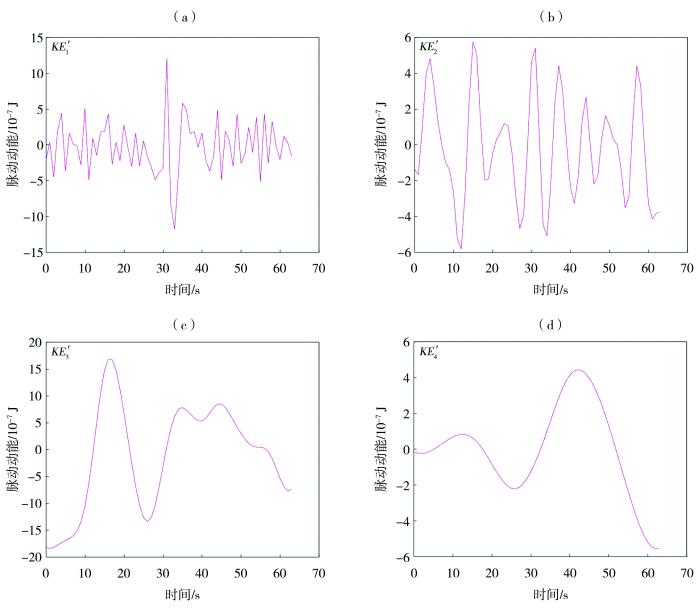
... [数据来自Tan等(2020)文献,测量高度0.05 m;物理量下标0为趋势项,1为脉动项,下同] ...
... (Data are sourced from the ref. (Tan et al., 2020), measured at 0.05 m height. Subscripts of variables 0 is for trend, 1 is for fluctuation, the same as follows) ...
... [数据来自Tan等(2020)文献,测量高度0.05 m] ...
... (Data are sourced from the ref. (Tan et al., 2020), measured at 0.05 m height) ...
... The fitting results of scaling exponents of energy spectrum of physical variables describing aeolian sand and dust motions under different measurement conditions
Tab.2 | 数据来源 | 高度/m | 物理量 | 序列数 | 均值 | 标准差 | 95%置信区间 | 物理量 | 序列数 | 均值 | 标准差 | 95%置信区间 |
| Wang et al.,2022 | 0.30 | U | 1 724 | 1.438 | 0.418 | [1.418, 1.457] | W | 1 724 | 1.336 | 0.491 | [1.313, 1.360 ] |
| 0.83 | 1.445 | 0.345 | [1.429, 1.461] | 1.360 | 0.456 | [1.339, 1.382 ] |
| 3.00 | 1.468 | 0.360 | [1.451, 1.485] | 1.404 | 0.508 | [1.380, 1.428] |
| Tan et al.,2020 | 0.05 | KE | 37 | 1.141 | 0.175 | [1.083, 1.200] | PC | 34 | 1.393 | 0.295 | [1.290, 1.496] |
| 0.12 | 37 | 1.110 | 0.193 | [1.046, 1.174] | 34 | 1.380 | 0.198 | [1.311, 1.449] |
| 0.38 | 18 | 1.038 | 0.165 | [0.956, 1.120] | 24 | 1.224 | 0.212 | [1.135, 1.314] |
| 0.80 | PC | 1 | 1.451 | | | | | | | |
| 0.70 | U | 1 006 | 1.192 | 0.055 | [1.188, 1.195] | W | 1 006 | 1.313 | 0.143 | [1.305, 1.322] |
| 2.00 | 1.313 | 0.143 | [1.305, 1.322] | 1.134 | 0.184 | [1.123, 1.146] |
| Wang et al., 2023 | 0.05 | KE | 30 | 1.021 | 0.208 | [0.943, 1.098] | PC | 23 | 1.234 | 0.145 | [1.172, 1.297] |
| 0.12 | 24 | 0.929 | 0.215 | [0.839, 1.020] | 28 | 1.176 | 0.186 | [1.104,1.248] |
| 0.38 | 15 | 0.992 | 0.138 | [0.916, 1.068] | 14 | 1.055 | 0.185 | [0.948,1.161] |
| 0.80 | 21 | 0.907 | 0.131 | [0.847, 0.966] | 15 | 1.121 | 0.137 | [1.045,1.197] |
| 1.41 | 19 | 0.781 | 0.183 | [0.692, 0.869] | 21 | 1.204 | 0.216 | [1.106,1.302] |
| 1.20 | U | 98 | 0.835 | 0.106 | [0.813, 0.856] | W | 98 | 0.590 | 0.089 | [0.572,0.608] |
| 2.80 | 0.891 | 0.100 | [0.871, 0.911] | 0.629 | 0.104 | [0.608,0.650] |
| 本研究 | 0.10 | DA | 11 | 1.513 | 0.228 | [1.360, 1.665] | DN | 12 | 1.015 | 0.210 | [0.882,1.149] |
| 0.20 | 7 | 1.400 | 0.192 | [1.224, 1.577] | 11 | 1.276 | 0.185 | [1.152,1.401] |
| 0.50 | 11 | 1.276 | 0.185 | [1.152, 1.401] | 18 | 0.965 | 0.164 | [0.883,1.046] |
| 1.00 | 23 | 0.922 | 0.199 | [0.837, 1.008] | 12 | 0.756 | 0.077 | [0.708,0.805] |
| 1.50 | 10 | 1.022 | 0.216 | [0.868, 1.176] | | | | |
| 2.00 | 15 | 0.901 | 0.108 | [0.842, 0.961] | 11 | 0.932 | 0.117 | [0.854, 1.010] |
| 0.50 | U | 486 | 1.187 | 0.043 | [1.183, 1.190] | W | 486 | 0.899 | 0.067 | [0.893, 0.905] |
| 1.00 | 1.214 | 0.042 | [1.211, 1.218] | 1.214 | 0.041 | [1.210, 1.218] |
4 讨论戈壁地表附近的沙尘运动由气流驱动.根据牛顿力学原理,沙尘颗粒的轨迹和运动速度应该能够被气流速度精确预测.目前,无论流沙地表,还是戈壁地表,瞬时输沙率都难以预测.主要原因可能在于地表附近湍流结构复杂多样、风沙流输运过程的间歇性特征、气流和沙粒在不同时空尺度上的相互作用.传统风沙输运模型中的摩阻速度代表了气流对地表的时均剪切力,不能描述瞬时气流场.本研究通过连续非零数据定义沙尘事件,克服了间歇性带来的困难,进而由Hilbert-Huang变换得到了特征物理量的能谱.符合幂次标度律的Hilbert边际谱意味着戈壁沙尘运动很可能像湍流那样建立统计理论,进而实现风沙运动的统计预测,克服瞬时输沙率预测的困难.各物理量的幂次律标度指数随高度变化则说明沙尘运动规律比壁湍流更复杂.本文的不足之处在于,风速和沙尘物理量的空间测量位置存在较大差异,难以从实验上测定戈壁气流和沙尘在采样间隔及更小时间尺度上的相互作用,进而揭示物理机制.利用更小尺寸与更高采样频率的传感器开展野外观测,并通过更先进的数学工具分析数据,可望克服这一缺陷.另外,弄清戈壁沙尘事件中风速、沙尘颗粒速度、浓度等物理量的概率密度是统计描述和预测的前提,亦有赖于将来的工作. ...
Field observation evidence for kink points in the vertical kinetic energy flux profiles of wind-blown sand over gobi and its significance
1
2021
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
Vertical flux density and frequency profiles of wind-blown sand as a function of the grain size over gobi and implications for aeolian transport processes
1
2022
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
The effect of roughness density of gobi beds on the entrainment of sediment by wind: A wind tunnel study
1
2019
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
Aeolian sand transport over gobi with different gravel coverages under limited sand supply: A mobile wind tunnel investigation
1
2013
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
Aeolian sediment transport over gobi: Field studies atop the Mogao Grottoes, China
1
2016
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
Unsteady saltation on Mars
1
2015
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
Aeolian sediment transport over sandy gobi: Field studies in the Nanhu gobi along the Hami-Lop Nor Railway
5
2023
... Datasets of aeolian sand and dust motions over Gobi and measurement conditions
Tab.1 | 数据来源 | 高度/m | 物理量 | 传感器(厂家) | 采样频率/Hz | 采样精度 |
| Wang et al.,2022 | 0.30、0.83、3.00 | U、V、W | WindMaster Pro(Gill) | 20 | 0.001 m·s-1 |
| Tan et al.,2020 | 0.05、0.12、0.38、0.80、1.38 | KE、PC | H11-Lin(Sensit) | 1 | 1×10-7 J·s-1、s-1 |
| 0.70、2.00 | U、φ、θ | Young-81000(RM Young) | 20 | 0.01 m·s-1、0.1° |
| Wang et al.,2023 | 0.05、0.12、0.38、0.80、1.41 | KE、PC | H11-Lin(Sensit) | 1 | 1×10-7 J·s-1、s-1 |
| 1.20、2.80 | U、V、W | WindMaster Pro(Gill) | 1 | 0.001 m·s-1 |
| 本研究团队 | 0.10、0.20、0.50、1.00、1.50、2.00 | DA、DN | DustTrak-II(TSI) | 0.2 | 0.001 mg·m-3 |
| 0.50、1.00 | U、V、W | Young-81000(RM Young) | 20 | 0.01 m·s-1 |
注:U为球坐标系下的风速大小或直角坐标系下的水平风速分量;V为直角坐标系下的另一个水平风速分量;W为垂向风速;φ为仰角,θ为方位角;KE为动能,PC为个数;DA为人工地表粉尘浓度,DN为天然地表粉尘浓度.下同. ...
... 3 )观测地点位于吐鲁番—哈密盆地东南部的南湖戈壁(92.77°E,42.25°N),36.59%的地表被8~10 mm大小的砾石所覆盖,处于中等风能环境中.仪器布设详见Wang等(2023)文献.该数据集共有19 799条记录,每条记录包含5个高度处的沙粒动能和个数与2个高度处的3个风速分量,详细描述及下载链接见Mendeley网站(https://doi.org/10.17632/mwyftts329.1). ...
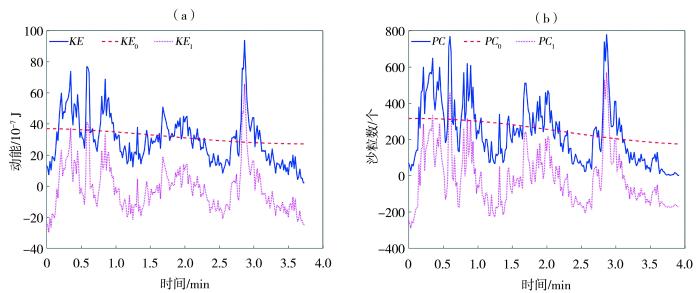
... [数据来自Wang等(2023)文献,测量高度0.05 m] ...
... (Data are sourced from the ref. (Wang et al., 2023), measured at 0.05 m height) ...
... The fitting results of scaling exponents of energy spectrum of physical variables describing aeolian sand and dust motions under different measurement conditions
Tab.2 | 数据来源 | 高度/m | 物理量 | 序列数 | 均值 | 标准差 | 95%置信区间 | 物理量 | 序列数 | 均值 | 标准差 | 95%置信区间 |
| Wang et al.,2022 | 0.30 | U | 1 724 | 1.438 | 0.418 | [1.418, 1.457] | W | 1 724 | 1.336 | 0.491 | [1.313, 1.360 ] |
| 0.83 | 1.445 | 0.345 | [1.429, 1.461] | 1.360 | 0.456 | [1.339, 1.382 ] |
| 3.00 | 1.468 | 0.360 | [1.451, 1.485] | 1.404 | 0.508 | [1.380, 1.428] |
| Tan et al.,2020 | 0.05 | KE | 37 | 1.141 | 0.175 | [1.083, 1.200] | PC | 34 | 1.393 | 0.295 | [1.290, 1.496] |
| 0.12 | 37 | 1.110 | 0.193 | [1.046, 1.174] | 34 | 1.380 | 0.198 | [1.311, 1.449] |
| 0.38 | 18 | 1.038 | 0.165 | [0.956, 1.120] | 24 | 1.224 | 0.212 | [1.135, 1.314] |
| 0.80 | PC | 1 | 1.451 | | | | | | | |
| 0.70 | U | 1 006 | 1.192 | 0.055 | [1.188, 1.195] | W | 1 006 | 1.313 | 0.143 | [1.305, 1.322] |
| 2.00 | 1.313 | 0.143 | [1.305, 1.322] | 1.134 | 0.184 | [1.123, 1.146] |
| Wang et al., 2023 | 0.05 | KE | 30 | 1.021 | 0.208 | [0.943, 1.098] | PC | 23 | 1.234 | 0.145 | [1.172, 1.297] |
| 0.12 | 24 | 0.929 | 0.215 | [0.839, 1.020] | 28 | 1.176 | 0.186 | [1.104,1.248] |
| 0.38 | 15 | 0.992 | 0.138 | [0.916, 1.068] | 14 | 1.055 | 0.185 | [0.948,1.161] |
| 0.80 | 21 | 0.907 | 0.131 | [0.847, 0.966] | 15 | 1.121 | 0.137 | [1.045,1.197] |
| 1.41 | 19 | 0.781 | 0.183 | [0.692, 0.869] | 21 | 1.204 | 0.216 | [1.106,1.302] |
| 1.20 | U | 98 | 0.835 | 0.106 | [0.813, 0.856] | W | 98 | 0.590 | 0.089 | [0.572,0.608] |
| 2.80 | 0.891 | 0.100 | [0.871, 0.911] | 0.629 | 0.104 | [0.608,0.650] |
| 本研究 | 0.10 | DA | 11 | 1.513 | 0.228 | [1.360, 1.665] | DN | 12 | 1.015 | 0.210 | [0.882,1.149] |
| 0.20 | 7 | 1.400 | 0.192 | [1.224, 1.577] | 11 | 1.276 | 0.185 | [1.152,1.401] |
| 0.50 | 11 | 1.276 | 0.185 | [1.152, 1.401] | 18 | 0.965 | 0.164 | [0.883,1.046] |
| 1.00 | 23 | 0.922 | 0.199 | [0.837, 1.008] | 12 | 0.756 | 0.077 | [0.708,0.805] |
| 1.50 | 10 | 1.022 | 0.216 | [0.868, 1.176] | | | | |
| 2.00 | 15 | 0.901 | 0.108 | [0.842, 0.961] | 11 | 0.932 | 0.117 | [0.854, 1.010] |
| 0.50 | U | 486 | 1.187 | 0.043 | [1.183, 1.190] | W | 486 | 0.899 | 0.067 | [0.893, 0.905] |
| 1.00 | 1.214 | 0.042 | [1.211, 1.218] | 1.214 | 0.041 | [1.210, 1.218] |
4 讨论戈壁地表附近的沙尘运动由气流驱动.根据牛顿力学原理,沙尘颗粒的轨迹和运动速度应该能够被气流速度精确预测.目前,无论流沙地表,还是戈壁地表,瞬时输沙率都难以预测.主要原因可能在于地表附近湍流结构复杂多样、风沙流输运过程的间歇性特征、气流和沙粒在不同时空尺度上的相互作用.传统风沙输运模型中的摩阻速度代表了气流对地表的时均剪切力,不能描述瞬时气流场.本研究通过连续非零数据定义沙尘事件,克服了间歇性带来的困难,进而由Hilbert-Huang变换得到了特征物理量的能谱.符合幂次标度律的Hilbert边际谱意味着戈壁沙尘运动很可能像湍流那样建立统计理论,进而实现风沙运动的统计预测,克服瞬时输沙率预测的困难.各物理量的幂次律标度指数随高度变化则说明沙尘运动规律比壁湍流更复杂.本文的不足之处在于,风速和沙尘物理量的空间测量位置存在较大差异,难以从实验上测定戈壁气流和沙尘在采样间隔及更小时间尺度上的相互作用,进而揭示物理机制.利用更小尺寸与更高采样频率的传感器开展野外观测,并通过更先进的数学工具分析数据,可望克服这一缺陷.另外,弄清戈壁沙尘事件中风速、沙尘颗粒速度、浓度等物理量的概率密度是统计描述和预测的前提,亦有赖于将来的工作. ...
Aeolian sediment transport over the Gobi with high gravel coverage under extremely strong winds in the Hundred Miles windy area along the Lanzhou-Xinjiang High-Speed Railway
4
2022
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
... Datasets of aeolian sand and dust motions over Gobi and measurement conditions
Tab.1 | 数据来源 | 高度/m | 物理量 | 传感器(厂家) | 采样频率/Hz | 采样精度 |
| Wang et al.,2022 | 0.30、0.83、3.00 | U、V、W | WindMaster Pro(Gill) | 20 | 0.001 m·s-1 |
| Tan et al.,2020 | 0.05、0.12、0.38、0.80、1.38 | KE、PC | H11-Lin(Sensit) | 1 | 1×10-7 J·s-1、s-1 |
| 0.70、2.00 | U、φ、θ | Young-81000(RM Young) | 20 | 0.01 m·s-1、0.1° |
| Wang et al.,2023 | 0.05、0.12、0.38、0.80、1.41 | KE、PC | H11-Lin(Sensit) | 1 | 1×10-7 J·s-1、s-1 |
| 1.20、2.80 | U、V、W | WindMaster Pro(Gill) | 1 | 0.001 m·s-1 |
| 本研究团队 | 0.10、0.20、0.50、1.00、1.50、2.00 | DA、DN | DustTrak-II(TSI) | 0.2 | 0.001 mg·m-3 |
| 0.50、1.00 | U、V、W | Young-81000(RM Young) | 20 | 0.01 m·s-1 |
注:U为球坐标系下的风速大小或直角坐标系下的水平风速分量;V为直角坐标系下的另一个水平风速分量;W为垂向风速;φ为仰角,θ为方位角;KE为动能,PC为个数;DA为人工地表粉尘浓度,DN为天然地表粉尘浓度.下同. ...
... 1 )观测地点位于吐鲁番—哈密盆地中部十三间房的天山冲洪积扇上(91.73°E,43.13°N),鹅卵石覆盖度高达87%左右,年平均风速7.13 m·s-1,最大瞬时风速56.60 m·s-1,年均大风(10 m高度处风速超过17.10 m·s-1)日数179 d(Cheng et al.,2015),处于高风能环境中.仪器布设详见Wang等(2022)文献,观测的物理量包括气温、气压、空气湿度、风速、输沙率等.本文仅分析一个由862 000条风速记录组成的子数据集. ...
... The fitting results of scaling exponents of energy spectrum of physical variables describing aeolian sand and dust motions under different measurement conditions
Tab.2 | 数据来源 | 高度/m | 物理量 | 序列数 | 均值 | 标准差 | 95%置信区间 | 物理量 | 序列数 | 均值 | 标准差 | 95%置信区间 |
| Wang et al.,2022 | 0.30 | U | 1 724 | 1.438 | 0.418 | [1.418, 1.457] | W | 1 724 | 1.336 | 0.491 | [1.313, 1.360 ] |
| 0.83 | 1.445 | 0.345 | [1.429, 1.461] | 1.360 | 0.456 | [1.339, 1.382 ] |
| 3.00 | 1.468 | 0.360 | [1.451, 1.485] | 1.404 | 0.508 | [1.380, 1.428] |
| Tan et al.,2020 | 0.05 | KE | 37 | 1.141 | 0.175 | [1.083, 1.200] | PC | 34 | 1.393 | 0.295 | [1.290, 1.496] |
| 0.12 | 37 | 1.110 | 0.193 | [1.046, 1.174] | 34 | 1.380 | 0.198 | [1.311, 1.449] |
| 0.38 | 18 | 1.038 | 0.165 | [0.956, 1.120] | 24 | 1.224 | 0.212 | [1.135, 1.314] |
| 0.80 | PC | 1 | 1.451 | | | | | | | |
| 0.70 | U | 1 006 | 1.192 | 0.055 | [1.188, 1.195] | W | 1 006 | 1.313 | 0.143 | [1.305, 1.322] |
| 2.00 | 1.313 | 0.143 | [1.305, 1.322] | 1.134 | 0.184 | [1.123, 1.146] |
| Wang et al., 2023 | 0.05 | KE | 30 | 1.021 | 0.208 | [0.943, 1.098] | PC | 23 | 1.234 | 0.145 | [1.172, 1.297] |
| 0.12 | 24 | 0.929 | 0.215 | [0.839, 1.020] | 28 | 1.176 | 0.186 | [1.104,1.248] |
| 0.38 | 15 | 0.992 | 0.138 | [0.916, 1.068] | 14 | 1.055 | 0.185 | [0.948,1.161] |
| 0.80 | 21 | 0.907 | 0.131 | [0.847, 0.966] | 15 | 1.121 | 0.137 | [1.045,1.197] |
| 1.41 | 19 | 0.781 | 0.183 | [0.692, 0.869] | 21 | 1.204 | 0.216 | [1.106,1.302] |
| 1.20 | U | 98 | 0.835 | 0.106 | [0.813, 0.856] | W | 98 | 0.590 | 0.089 | [0.572,0.608] |
| 2.80 | 0.891 | 0.100 | [0.871, 0.911] | 0.629 | 0.104 | [0.608,0.650] |
| 本研究 | 0.10 | DA | 11 | 1.513 | 0.228 | [1.360, 1.665] | DN | 12 | 1.015 | 0.210 | [0.882,1.149] |
| 0.20 | 7 | 1.400 | 0.192 | [1.224, 1.577] | 11 | 1.276 | 0.185 | [1.152,1.401] |
| 0.50 | 11 | 1.276 | 0.185 | [1.152, 1.401] | 18 | 0.965 | 0.164 | [0.883,1.046] |
| 1.00 | 23 | 0.922 | 0.199 | [0.837, 1.008] | 12 | 0.756 | 0.077 | [0.708,0.805] |
| 1.50 | 10 | 1.022 | 0.216 | [0.868, 1.176] | | | | |
| 2.00 | 15 | 0.901 | 0.108 | [0.842, 0.961] | 11 | 0.932 | 0.117 | [0.854, 1.010] |
| 0.50 | U | 486 | 1.187 | 0.043 | [1.183, 1.190] | W | 486 | 0.899 | 0.067 | [0.893, 0.905] |
| 1.00 | 1.214 | 0.042 | [1.211, 1.218] | 1.214 | 0.041 | [1.210, 1.218] |
4 讨论戈壁地表附近的沙尘运动由气流驱动.根据牛顿力学原理,沙尘颗粒的轨迹和运动速度应该能够被气流速度精确预测.目前,无论流沙地表,还是戈壁地表,瞬时输沙率都难以预测.主要原因可能在于地表附近湍流结构复杂多样、风沙流输运过程的间歇性特征、气流和沙粒在不同时空尺度上的相互作用.传统风沙输运模型中的摩阻速度代表了气流对地表的时均剪切力,不能描述瞬时气流场.本研究通过连续非零数据定义沙尘事件,克服了间歇性带来的困难,进而由Hilbert-Huang变换得到了特征物理量的能谱.符合幂次标度律的Hilbert边际谱意味着戈壁沙尘运动很可能像湍流那样建立统计理论,进而实现风沙运动的统计预测,克服瞬时输沙率预测的困难.各物理量的幂次律标度指数随高度变化则说明沙尘运动规律比壁湍流更复杂.本文的不足之处在于,风速和沙尘物理量的空间测量位置存在较大差异,难以从实验上测定戈壁气流和沙尘在采样间隔及更小时间尺度上的相互作用,进而揭示物理机制.利用更小尺寸与更高采样频率的传感器开展野外观测,并通过更先进的数学工具分析数据,可望克服这一缺陷.另外,弄清戈壁沙尘事件中风速、沙尘颗粒速度、浓度等物理量的概率密度是统计描述和预测的前提,亦有赖于将来的工作. ...
Unsteady aeolian saltation
4
2018
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... ).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... )、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... 按照沙尘事件定义和时间序列选取方法,从4个数据集中筛选出1~37个时长不等的沙尘事件,并依次选取1 724、1 006、98和486个风速序列.实际计算表明,脉动项个数m一般为4~10.每个风速脉动项具有不同的特征时间尺度,彼此叠加即可构成复杂的湍流相干结构.除了地表影响,沙尘脉动主要由风速脉动引起.如果表征风与沙的脉动项之间的小波相干系数较大,那么二者之间大致成正比例关系(Wang et al.,2018).每个脉动项都有自己的特征频率,可通过构造复频率方式定量描述风与沙脉动项之间的相互作用(Wang,2024).不同于小波变换,Hilbert-Huang变换尚缺乏严格的数学基础(de Souza et al.,2022).这里仅将模态分解算法作为计算Hilbert谱的一种有效手段. ...
Some statistical properties of aeolian saltation
6
2024
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... ).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... ;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... 只有在大于起动风速时,才会有风沙活动.因此,沙尘输运过程具有非常显著的间歇特点.只有先定义沙尘事件,才能进行精细的数据分析.当没有沙尘活动时,表1中的跃移沙粒动能KE、个数PC、粉尘浓度DA和DN均为零.参照对流沙地表附近风沙事件的定义(Wang,2024),这里仍将任意一个沙尘特征物理量在某段时间内均不为零的序列定义为一个戈壁沙尘事件.据此,沙尘事件持续的最短时间为一个采样间隔,即表1中采样频率的倒数.除了采样频率,沙尘事件还依赖于传感器灵敏度和精度等.在相同环境条件下,不同传感器探测到的沙尘事件时间和强度往往有所不同,从而由观测数据定义的沙尘事件有一定程度的不确定性.如果沙尘运动服从某种统计规律,那么由不同时间序列得到的统计特征及其定量描述中的概率密度函数和相关参数应该一致. ...
... 按照沙尘事件定义和时间序列选取方法,从4个数据集中筛选出1~37个时长不等的沙尘事件,并依次选取1 724、1 006、98和486个风速序列.实际计算表明,脉动项个数m一般为4~10.每个风速脉动项具有不同的特征时间尺度,彼此叠加即可构成复杂的湍流相干结构.除了地表影响,沙尘脉动主要由风速脉动引起.如果表征风与沙的脉动项之间的小波相干系数较大,那么二者之间大致成正比例关系(Wang et al.,2018).每个脉动项都有自己的特征频率,可通过构造复频率方式定量描述风与沙脉动项之间的相互作用(Wang,2024).不同于小波变换,Hilbert-Huang变换尚缺乏严格的数学基础(de Souza et al.,2022).这里仅将模态分解算法作为计算Hilbert谱的一种有效手段. ...
... 表2列出了不同观测条件下标度指数的平均值、标准差和根据t分布计算的95%置信区间.作为气流场的边界,地面影响着附近的风速和沙粒运动.空中运动的沙尘颗粒也改变了湍动能的传递和耗散过程.因此,沙尘运动各物理量标度指数与净气流速度的“-1”或“-5/3”有所差别.从均值看,跃移沙粒动能KE的指数大致随高度上升而下降;沙粒个数PC的指数随高度上升而下降(第2数据集)或者先降后升(第3数据集).这是因为前者缺少0.80 m及以上高度的时间序列.人工戈壁观测场粉尘浓度的指数基本随高度上升而下降,天然观测场的则无明显规律.从数值上看,沙尘特征量和风速的各指数差别较大,范围分别为0.78~1.51和0.59~1.47.此前,利用Hilbert-Huang变换得到的流沙地表4 cm高度内跃移沙粒数序列和平坦地面上10 m高度处水平风速序列的Hilbert边际谱指数分别为1(Wang,2024)和1.27(Wei et al.,2017),包含在表2中的能谱指数平均值范围之内. ...
Intermittency of aeolian saltation
2
2014
... 瞬时输沙率难以预测的根本原因在于气流与运动沙粒之间同时存在不同时空尺度的复杂耦合作用(Wang,2024).风沙流在空间上表现为一丝一缕的条带状(Baas,2008),在时间上具有明显的间歇性(Stout and Zobeck,1997;Davidson-Arnott et al.,2012;Wang et al.,2014;Sherman et al.,2018;Tan et al.,2020)和非平稳性(Butterfield,1998;Spies et al.,2000;Wang and Zheng,2015;Wang et al.,2018).这些特征给瞬时风沙流的数学描述与实验数据分析带来极大挑战.从数学描述角度看,虽然平均风速大于起动风速所占的时间比例(Stout and Zobeck,1997)、跃移活动参数(Davidson-Arnott et al.,2012)、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
... )、沙粒浓度峰度(Wang et al.,2014)等均被作为间歇性指标,但因缺乏统一的测量和量化标准而使不同实验结果之间难以比较(Sherman et al.,2018).对于驱动沙尘运动的湍流,流体力学研究者们已经给出成熟的统计描述.对沙尘运动进行统计预测可能是替代瞬时输沙率预测的可行方案.物理量随时空尺度的变化规律称为标度律.在湍流统计理论中,标度律专指高雷诺数流动的速度结构函数随空间两点间隔的幂次律.著名的K41理论给出了各向同性均匀湍流在惯性区的标度指数为‒5/3.在阿拉善高原两处流动沙丘迎风坡顶的野外观测初步显示,流沙地表附近几乎饱和风沙流的跃移输沙密度也存在类似规律(Wang,2024).戈壁地表的风沙流与流沙地表的差别很大,虽然进行了大量观测,但尚未探讨可能存在的标度律.从实验数据分析角度看,沙尘和气流的运动都是非平稳的,统计特征随时间而变(Wang et al.,2018).许多基于线性或平稳过程发展起来的数学工具不适合非平稳过程.适用于风沙物理量非平稳时间序列分析的有效方法包括小波变换(Baas,2006;Ellis and Sherman,2023)、Hilbert-Huang变换(Wang et al.,2018;Wang,2024)和动态时间规整等.其中,Hilbert-Huang变换的适应性很强,提取出的信号特征通常具有明确的物理意义(Huang and Wu,2008;de Souza et al.,2022).本文借鉴湍流的统计描述思想,利用Hilbert-Huang变换分析处理中国西部典型戈壁区的观测数据,探讨近地表气流、沙和尘物理量的统计特征,以期为沙尘运动的统计预测提供方法参考和数据支撑. ...
Investigation of turbulence behaviour in the stable boundary layer using arbitrary-order Hilbert spectra
1
2017
... 表2列出了不同观测条件下标度指数的平均值、标准差和根据t分布计算的95%置信区间.作为气流场的边界,地面影响着附近的风速和沙粒运动.空中运动的沙尘颗粒也改变了湍动能的传递和耗散过程.因此,沙尘运动各物理量标度指数与净气流速度的“-1”或“-5/3”有所差别.从均值看,跃移沙粒动能KE的指数大致随高度上升而下降;沙粒个数PC的指数随高度上升而下降(第2数据集)或者先降后升(第3数据集).这是因为前者缺少0.80 m及以上高度的时间序列.人工戈壁观测场粉尘浓度的指数基本随高度上升而下降,天然观测场的则无明显规律.从数值上看,沙尘特征量和风速的各指数差别较大,范围分别为0.78~1.51和0.59~1.47.此前,利用Hilbert-Huang变换得到的流沙地表4 cm高度内跃移沙粒数序列和平坦地面上10 m高度处水平风速序列的Hilbert边际谱指数分别为1(Wang,2024)和1.27(Wei et al.,2017),包含在表2中的能谱指数平均值范围之内. ...
The varying fetch effect of aeolian sand transport above a gobi surface and its implication for gobi development process
3
2022
... 我国戈壁主要分布在西北极端干旱区,面积约5.695×105 km2(王涛和陈广庭,2008).戈壁地区往往地势平坦,植被稀疏,强风及其携带的沙尘经常破坏基础设施.以新疆戈壁大风区的铁路系统为例,风沙危害具体表现为降低能见度、磨蚀轮轨、损坏车窗、掩埋线路、吹翻列车等(尹永顺,1990;Cheng et al.,2015;Shu et al.,2022).充分了解戈壁沙尘运动基本规律是科学开展其相关危害预警与防治的重要前提.在过去30余年内,国内风沙工作者以野外观测和室内风洞为主要研究手段,对这种现象的认识越来越深入.与流沙地表附近的风沙流相同,戈壁风沙流的常规研究内容也是起动机制、跃移轨迹、发展过程、风沙流结构与输沙率等.其中,处于核心地位的输沙率指单位时间单位宽度内顺风向输运的沙物质质量.戈壁风沙流输沙特征的主要控制因素包括风况和沙源丰富度(柳本立等,2010)、地表物质机械组成(Tan et al.,2022)、砾石盖度(Liu and Kimura,2018;Tan et al.,2019;Wang et al.,2022)和风程(张正偲等,2011;Zhang et al.,2022)等.地表紧实且风速较大导致跃移轨迹具有起跳角、高度和长度都很大的突出特点(邹学勇等,1995).实验结果表明,跃移轨迹的高度和长度可达到4.8和9.0 m(Liu et al.,2021).因沙源有限,地表的松散沙粒难以满足风的最大搬运能力,风沙流常处于非饱和状态,出现异常结构.早期的集沙仪与风速廓线仪观测表明,输沙通量在一定高度处呈现最大值并随风速的增加而增大(屈建军等,2005;张克存等,2005),沙粒的质量浓度则随高度增加而单调下降(蒋富强等,2010;李凯崇等,2010).多项式函数、指数函数和幂函数均被用于描述风沙流结构(屈建军等,2012;黄雨晖等,2019).近年来的碰撞传感器和超声风速仪观测显示,沙粒数随高度呈指数形式递减,跃移沙动能通量是高度的Pearson VII函数(Tan et al.,2021).实际上,输沙率和风沙流结构实验结果均与观测时间有关.在分钟及更长时间尺度上,平均输沙率与风速之间具有良好对应关系.1 min的平均输沙率符合Owen公式(Tan et al.,2013;Tan et al.,2016);10 min到数小时的平均输沙率是风速的指数(王志强等,2010)或低阶多项式函数(刘旭阳等,2020);以Bagnold公式为基础,可建立年际尺度的输沙量算法(王旭,2019).目前,在秒及以下的短时间尺度上预测输沙率是公认难题(Chamecki and Kok,2023),难以在戈壁风沙流瞬时输沙率与风速之间建立对应关系(Tan et al.,2020). ...
... 4 )观测地点位于党河南山以北的阿克塞盆地中(94.40°E,39.70°N),分别在去除植被并对上风向地表实施化学固沙措施的人工观测场和约15%植被盖度的自然观测场中进行观测,所测量的PM10质量浓度分别称为人工地表和天然地表粉尘浓度.两个观测场地表物质均以粗砂和中砂为主,质量比83%~91%.受地形影响,观测地点处于低风能环境中.对观测场的具体描述见相关文献(刘旭阳等,2020;Zhang et al.,2022).该数据集包括14 d人工观测场和5 d自然观测场内5个高度处的PM10质量浓度和2个高度处的3个风速分量,由本研究团队于2017年3月16日—5月2日期间陆续观测获得. ...
... 0.10 m高度处两组粉尘浓度时间序列的分解结果见图5,模态项数均为6.其中,人工地表粉尘浓度专指在去除植被且对上风向边界处地表做过不可蚀处理的观测场(刘旭阳等,2020;Zhang et al.,2022)内测量的粉尘浓度.因为并非同步观测,图5中人工和天然戈壁观测场的粉尘浓度不具有可比性.在1 h内,人工观测场近地表粉尘浓度大致表现为先增加后稳定再下降的趋势,因趋势项数值较低,脉动现象比较明显;天然观测场的沙尘浓度一直呈缓慢上升趋势,因为趋势项数值较大,脉动项更像在零点附近波动的噪声,实际并非如此,脉动项振幅与人工观测场很接近,亦有一定的动态规律性. ...