0 引言
冰雹是我国主要的灾害性天气之一,特别是低纬高原区域冰雹灾害多发、频发,具有局地性强、生命史短、早识别难等特点,极易对烟叶、茶叶、特色经果林、设施农业等造成毁灭性破坏(冯晓莉等,2021)。冰雹识别预警越早,冰雹防御效果则越好,利用卫星观测资料实时动态研判和争取更多冰雹预警提前量意义重大。
多年来国内外针对冰雹识别预警技术开展了大量研究。如部分研究建立了冰雹和稳定指数间的关系,并能利用这些关系有效预测对流天气(Neumann,1971;Reap and Foster,1979;Johns and DoswellⅢ,1992;Lee and Passner,1993;McNulty,1995;Tudurí and Ramis,1997),但这些预报技术具有显著的地域特征,当这些指数被应用到其他地区时,通常预报效果会明显下降(López et al.,2001;López et al.,2007)。部分美国和欧洲学者也在寻求能在不同区域都能有效预测对流的指数(Collier and Liliey,1994;Huntrieser et al.,1997),但效果并不十分理想。Reap和Macgorman(1989)研究云地闪和对流之间的关系和特征时发现闪电对对流云团的产生、发展有一定的指示作用;López等(2001)尝试将稳定指数与探空仪采集的气象参数一同作为参数训练冰雹识别模型,并取得一定进展;Orlanski(1975)建立了能量不稳定区域和对流触发机制的冰雹识别模型,但此识别模型会出现较多的空报;López等(2007)基于西班牙北部埃布罗河谷地区C波段雷达与探空仪观测资料建立了短期预报Logistics回归模型并开展冰雹识别研究,该模型对冰雹识别准确率达87%,冰雹误报率为18%;彭宇翔等(2021)以FY-2G卫星反演产品为输入参数建立决策树模型,对2020年贵州降雹进行识别,发现该模型降雹识别准确率达80%。此外,通过数据挖掘能实现变量特征提取,采用的方法如LASSO(Tibshirani,1996)、SCAD(Fan and Li,2001)、Adaptive Lasso(Zou,2006)及Dantzig Selector(Candes and Tao,2007)等,这些方法对连续性响应变量的高维数据处理效果较好,但在二值响应变量的应用中效果并不理想。因此,需要寻找新的方法对所分析数据进行降维和变量筛选,Mai 和Zou(2013)提出了Kolmogorov变量筛选过滤器,针对二值响应变量涉及的预测变量进行筛选。
目前,国内外对冰雹天气过程的研究主要针对其发展演变的宏微观物理特征及个例分析开展,FY-2G卫星虽然已投入使用多年,但缺乏基于其反演产品建立定量化的冰雹识别指标并开展系统化冰雹智能识别等方面的研究。同时,支持向量机作为一种典型的机器学习算法,已广泛应用于医学、金融及空间天气(Lu et al.,2016;彭宇翔等,2016)等领域,但它在冰雹快速识别预警中的应用还处于初级阶段,特别是气候变化对大气环境影响深远(张强等,2010;冯蜀青等,2019;朱生翠等,2020;易雪等,2021;曹晓云等,2022;王姝等,2024),近年来冰雹天气多发、频发,冰雹识别技术需求更显突出。本文基于支持向量机模型利用FY-2G卫星提供的反演产品开展智能冰雹识别研究,并利用Kolmogorov变量筛选过滤器对模型输入变量进行筛选,分析利用不同核函数以及进行变量筛选前后支持向量机模型对非降雹点与降雹点的识别准确率,验证支持向量机模型和数据挖掘技术对冰雹识别的有效性与可靠性。
1 资料
风云二号系列气象卫星是我国研制的第一代静止气象卫星,共计发射6颗,这些气象卫星与极轨卫星构成了我国气象卫星的主要应用体系。FY-2G作为风云二号系列的03批次卫星中的第2颗,是现阶段我国人工影响天气业务主要使用的气象卫星之一,其观测数据对人工影响天气业务工作的顺利开展非常重要。中国气象局人工影响天气中心以FY-2G卫星观测资料为基础,提供的7项反演产品(云顶高度、云顶温度、过冷层厚度、光学厚度、有效粒子半径、液水路径、黑体亮温)为我国人工影响天气监测和预警工作提供了有力支撑。
采用贵州省2020—2022年30个冰雹日的368组FY-2G卫星7项反演产品数据,这些数据包含184组降雹点与184组未降雹点资料。将每一个降雹点降雹前后15 min内的反演产品近似作为该点降雹时刻的反演数据。同时,随机选取同一冰雹过程中的非冰雹云(未发现降雹区域的云系)对应的反演产品作为对比组,且降雹点和未降雹点数量保持一致。
2 研究方法
基于FY-2G卫星提供的7项反演产品开展智能冰雹识别研究,分析各解释变量与响应变量的关联性,并剔除相关性较弱的变量开展冰雹识别,提升模型的有效性和运行效率。
2.1 Kolmogorov变量筛选过滤器
引入Mai和Zou(2013)建立的Kolmogorov变量筛选过滤器,开展冰雹识别的解释变量筛选。其主要思路:对
式中:
2.2 支持向量机
式中:
SVM的最主要目标是实现泛化误差界的最小化,而泛化误差界则是由结构风险(模型的复杂性)和经验风险(模型的训练误差)共同组成,因此泛化误差界表达式如下:
式中:
该限制条件的优化可以通过拉格朗日乘子解决。因此,公式(2)可转换为
式中:
核函数有很多种,常用的主要有Radial Basis Function(RBF)核函数、Linear核函数、Sigmoid核函数等。其中,RBF核函数通过计算欧几里得距离的平方来度量两个特征向量之间的相似性;Linear核函数是最常见、最简单的SVM的核函数,这个核函数返回一个线性超平面,它被用作分离类的决策边界,通过计算特征空间中两个输入向量的点积得到超平面;Sigmoid函数理论上擅长映射输入值并返回0到1之间的值,该函数通常用于神经网络中,其中s形函数作为分类的激活函数。基于不同种类的核函数所建立的SVM模型预测预报性能差别很大(Yang et al.,2006),为建立冰雹识别性能最优的SVM模型,本研究基于RBF核函数、Linear核函数、Sigmoid核函数分别建立RBF-SVM模型、L-SVM模型和S-SVM模型,通过检验对比,选取最优的冰雹识别模型。
3 结果与分析
3.1 数据分布特征
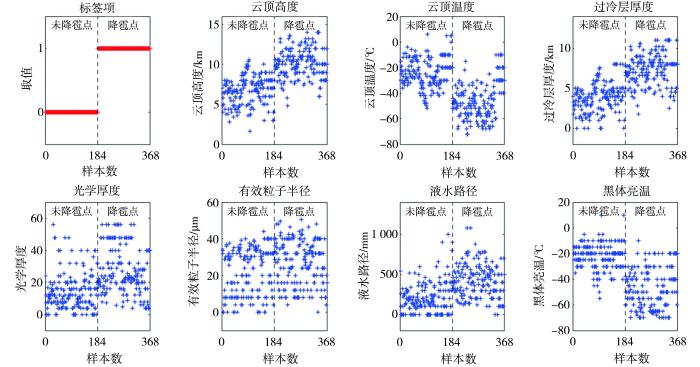
将贵州省2020—2022年30个冰雹日的368组FY-2G卫星反演产品数据依次排列,前184组为未降雹点数据(标记为0),后184组为降雹点数据(标记为1)。图1为未降雹点与降雹点分类标签数据,以及FY-2G卫星的7项反演产品数据分布,可以看出虽然这些产品的分布能体现出一些特征,但仅仅依靠数据分布无法直观识别冰雹。
图1
图1
数据分类与反演产品分布散点图
Fig.1
Scatter diagrams of data classification and inversion products distribution
3.2 识别结果对比
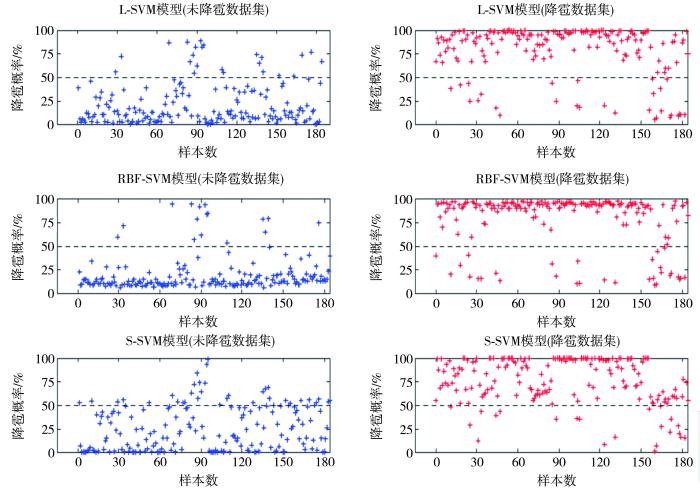
基于SVM模型和有关算法,分别利用Linear核函数、RBF核函数、Sigmoid核函数建立L-SVM模型、RBF-SVM模型与S-SVM模型,采用7-Fold交叉验证(即将整个数据集分为7个部分,每次都用其中6个部分建立模型,剩余1个部分进行检验,从而获得整个数据集的预测结果)检验模型识别性能。图2为3个模型对368组数据的识别结果分布,将50%作为界限(图2中虚线),当模型识别出的冰雹概率超过50%时认为该点会出现降雹,当模型识别的冰雹概率低于50%时,认为不会降雹。可以看出,3个模型均能有效识别大部分降雹点和未降雹点。由3个模型识别结果统计(表1)可知,对于184组未降雹点:L-SVM模型正确识别162组,错误识别22组,识别准确率为88.04%;RBF-SVM模型正确识别169组,错误识别15组,识别准确率为91.85%;S-SVM模型正确识别134组,错误识别50组,识别准确率为72.83%。对于184组降雹点:L-SVM模型正确识别155组,错误识别29组,识别准确率为84.24%;RBF-SVM模型正确识别153组,错误识别31组,识别准确率为83.15%;S-SVM模型正确识别164组,错误识别20组,识别准确率为89.13%。对于368组未降雹和降雹数据的总识别准确率RBF-SVM模型最高(87.50%),其次为L-SVM模型(86.14%),S-SVM模型最低(80.98%)。
图2
图2
L-SVM模型、RBF-SVM模型与S-SVM模型对未降雹点与降雹点识别结果分布
(虚线为识别概率50%分界线)
Fig.2
Distribution of hail and non hail points identification results based on L-SVM model, RBF-SVM model and S-SVM model
(The dotted line is the boundary line of 50% identification probability)
表1 3个模型识别结果统计
Tab.1
| 模型 | 分类 | 样本数量 | 识别为未降雹 | 识别为降雹 | 未降雹点识别准确率/% | 降雹点识别准确率/% | 总识别准确率/% |
|---|---|---|---|---|---|---|---|
| L-SVM | 未降雹 | 184 | 162 | 22 | 88.04 | 86.14 | |
| 降雹 | 184 | 29 | 155 | 84.24 | |||
| RBF-SVM | 未降雹 | 184 | 169 | 15 | 91.85 | 87.50 | |
| 降雹 | 184 | 31 | 153 | 83.15 | |||
| S-SVM | 未降雹 | 184 | 134 | 50 | 72.83 | 80.98 | |
| 降雹 | 184 | 20 | 164 | 89.13 |
3.3 模型识别概率分布
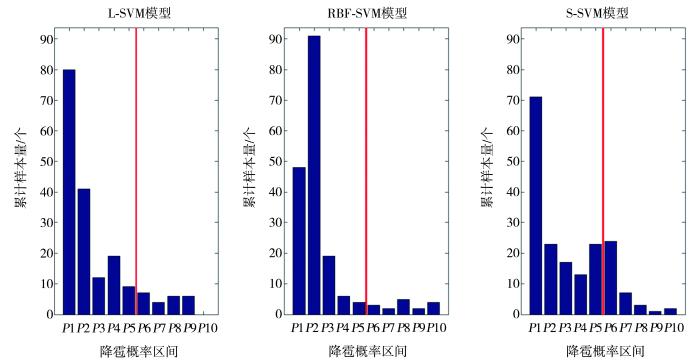
当模型识别概率P处于[0,50]%区间时,认为模型将该点识别为未降雹点;P处于(50,100]%区间时,则认为模型将该点识别为降雹点。当P越接近50%时,在某些特定情况下越容易引起误判;而P越接近0%或100%时,引起误判的概率越小。因此,模型识别概率的分布一定程度上能体现模型的识别性能。图3~4分别为模型对未降雹点和降雹点的识别概率分布,横轴P1表示0%≤P≤10%,P2表示10%<P≤20%,P3表示20%<P≤30%,P4表示30%<P≤40%,P5表示40%<P≤50%,P6表示50%<P≤60%,P7表示60%<P≤70%,P8表示70%<P≤80%,P9表示80%<P≤90%,P10表示90%<P≤100%。对于未降雹点,P1~P5为识别准确区间(红色竖线左侧区域);对于降雹点,P6~P10为识别准确区间(红色竖线右侧区域)。
图3
图3
3个模型对未降雹点的识别概率分布
(红色竖线为识别概率50%分界线,下同)
Fig.3
The distribution of three models’recognition probability for non-hail spots
(The red vertical line is the boundary line of 50% identification probability, the same as below)
图4
图4
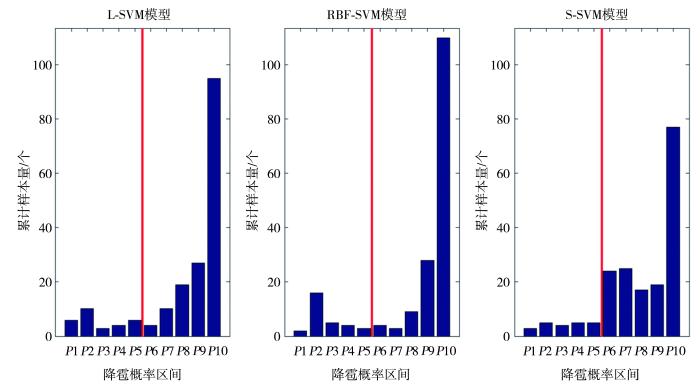
3个模型对降雹点的识别概率分布
Fig.4
The distribution of three models’ recognition probability for hail spots
对于未降雹点,由图3可知,L-SVM模型的识别概率分布最集中的是P1区间,其次是P2、P4、P3区间,其余区间样本量均小于10个;RBF-SVM模型识别概率分布最集中的是P2区间,其次是P1、P3区间,其余区间样本量均小于10个;S-SVM模型识别概率分布最集中的是P1区间,P6、P2、P5区间样本量较为接近,且均超过20个,然后是P3、P4区间,其余区间样本量均小于10个,由于较多的未降雹点样本被识别到P6、P5区间,因此导致S-SVM模型对未降雹点样本的识别准确率低于L-SVM模型和RBF-SVM模型。
对于降雹点,由图4可知,L-SVM模型的识别概率分布最集中的是P10区间,其次是P9、P8区间,其余区间样本量均小于10个;RBF-SVM模型识别概率分布最集中的是P10区间,其次是P9、P2区间,其余区间样本量均小于10个,P2区间样本数较多一定程度上导致RBF-SVM模型为3个模型中对降雹点识别准确率最低的模型;S-SVM模型识别概率分布最集中的是P10区间,其次为P7、P6、P9、P8区间,且样本量较为接近,其他区间样本量均少于5个。虽然对于降雹点S-SVM模型的识别准确率最高,但较多的样本分布在临界值(50%)附近区间(P6和P7),可能会导致在某些特定情况下该模型对降雹点识别准确率降低。
3.4 模型输入变量优化
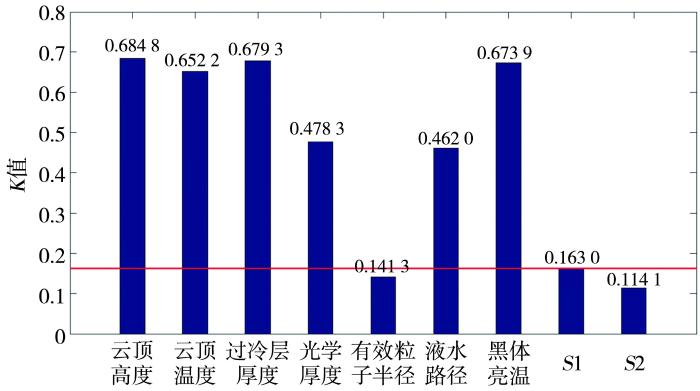
选用Kolmogorov变量筛选过滤器深度挖掘FY-2G卫星7项反演产品与降雹的关联性,关联性越高数值越接近1,关联性越低则越接近0。为明确变量选择标准,生成2个同维度的随机变量(S1和S2),利用公式(1)计算出7项反演产品及2个随机变量与是否降雹的Kolmogorov值(简称“K值”)。2个随机变量的生成与是否降雹没有关联性,因此将2个随机变量中最大的K值(K0)作为分界线,K值小于K0的反演产品与是否降雹没有关联性。
由图5可见,随机变量S1和S2的K值分别为0.163 0和0.114 1,因此K0=0.163 0,7项反演产品中仅有效粒子半径的K值小于K0,其余产品的K值均远高于K0,即有效粒子半径与降雹没有关联性,其余6项反演产品与是否降雹明显相关。
图5
图5
FY-2G卫星7项反演产品与2个随机变量(S1和S2)的K值
Fig.5
The K values of 7 inversion products of FY-2G satellite and 2 random variables (S1 and S2)
3.5 输入变量优化前后识别结果对比
以Kolmogorov变量筛选过滤器选定的FY-2G卫星6项反演产品(云顶高度、云顶温度、过冷层厚度、光学厚度、液水路径、黑体亮温)作为优化后的参数作为模型输入,分别利用LK-SVM模型、RBFK-SVM模型与SK-SVM模型,对184组降雹点与184组未降雹点进行识别,并采用7-Fold交叉验证获取全序列的识别结果,检验模型识别性能,识别结果见表2。
表2 变量优化前后模型识别结果统计
Tab.2
| 模型 | 未降雹点识别准确率 | 降雹点识别 准确率 | 总识别 准确率 |
|---|---|---|---|
| L-SVM | 88.04 | 84.24 | 86.14 |
| LK-SVM | 88.59 | 84.24 | 86.41 |
| RBF-SVM | 91.85 | 83.15 | 87.50 |
| RBFK-SVM | 92.93 | 83.70 | 88.04 |
| S-SVM | 72.83 | 89.13 | 80.98 |
| SK-SVM | 92.93 | 79.35 | 86.14 |
对于未降雹数据集,利用Kolmogorov变量筛选过滤器优化变量输入后各模型的准确率均有所提升。其中,L-SVM模型输入变量优化前后识别准确率分别为88.04%、88.59%;RBF-SVM模型优化前、后识别准确率分别为91.85%、92.93%;S-SVM模型输入变量优化后识别准确率提升最明显,从72.83%提升到92.93%。
对于降雹点数据集,L-SVM模型输入变量优化前后识别准确率没有变化(84.24%);RBF-SVM模型识别准确率为83.15%,输入变量优化后识别准确率略微提升到83.70%;S-SVM模型识别准确率为89.13%,经过输入变量优化后识别准确率反而明显下降至79.35%。
对于降雹点和未降雹点所有368组数据,经过变量筛选后,模型识别准确率均有不同程度上升,L-SVM模型识别准确率为86.14%,经过输入变量优化后提升不明显(86.41%);RBF-SVM模型识别准确率为87.50%,优化后识别准确率提升到88.04%;S-SVM模型识别准确率为80.98%,输入变量优化后提升最明显,识别准确率达86.14%。
4 结论
本文基于支持向量机Linear核函数、RBF核函数、Sigmoid核函数建立SVM模型开展冰雹识别研究,在对样本识别结果的检验过程中均采用交叉验证方法提升模型识别结果的可靠性,并利用Kolmogorov变量筛选过滤器优化变量输入,对比优化前后模型的识别准确率,得到以下具体结论。
1)基于支持向量机Linear核函数、RBF核函数、Sigmoid核函数建立的SVM模型均能有效解决基于FY-2G卫星资料的冰雹识别问题,且对于降雹点和未降雹点的识别准确率最低超过70%,最高超过90%。
2)RBF-SVM模型和L-SVM模型的识别稳定性优于S-SVM模型,在实际使用中其识别结果更可靠。
3)Kolmogorov变量筛选过滤器优化变量输入后,各模型对总数据集和未降雹点数据集的识别准确率均有所提升;对于降雹点数据集优化模型变量输入后,RBF-SVM模型、L-SVM模型识别准确率提升不明显,而S-SVM模型识别准确率反而明显下降。出现这种现象的原因可能是解释变量数量较少导致每个解释变量对结论的影响较大,且基于不同核函数的SVM模型从变量和样本中提取的特征存在差异。
4)对于未降雹点数据集,识别效果最好的是输入变量优化后的RBF-SVM模型和S-SVM模型,准确率均达92.93%;对于降雹点数据集,识别效果最好的是S-SVM模型;对总数据集而言,识别效果最好的是输入变量优化后的RBF-SVM模型。因此,综合识别效果最好的是输入变量优化后的RBF-SVM模型,如果识别降雹区域的话则主要关注S-SVM模型的识别结果。
参考文献
The dantzig selector: Statistical estimation when p is much larger than n
[J].
Forecasting thunderstorm initiation in north-west Europe using thermodynamic indices, satellite and radar data
[J].
Variable selection via nonconcave penalized likeli-hood and its oracle properties
[J].
Comparison of traditional and newly developed thunderstorm indices for Switzerland
[J].
Severe local storms forecasting
[J].
The development and verification of TIPS: An expert system to forecast thunderstorm occurrence
[J].
Support vector machine combined with distance correlation learning for Dst forecasting during intense geomagnetic storms
[J].
A short-term forecast model for hail
[J].
CAPE values and hailstorms on northwestern Spain
[J].
The Kolmogorov filter for variable screening in high-dimensional binary classification
[J].
Severe and convective weather: A central region forecasting challenge
[J].
The thunderstorm forecasting system at the kennedy space center
[J].
A rational subdivision of scales for atmospheric processes
[J].
Automated 12-36 hour probability forecasts of thunderstorms and severe local storms
[J].
Cloud-to-ground lightning: Climatological characteristics and relationships to model fields, radar observations, and severe local storms
[J].
Regression shrinkage and selection via the lasso
[J].
The environments of significant convective events in the western Mediterranean
[J].
Nemani, prediction of continental-scale evapotranspiration by combining MODIS and AmeriFlux data through support vector machine
[J].
The adaptive lasso and its oracle properties
[J].