基于随机森林算法的青藏高原东北边坡输电线路覆冰厚度预报模型

doi:10.11755/j.issn.1006-7639-2025-03-0488

基于随机森林算法的青藏高原东北边坡输电线路覆冰厚度预报模型

吕玫霞^,, 闫昕旸, 何金梅^,, 程鹏, 王小勇, 李晓琴

甘肃省气象服务中心，甘肃兰州 730020

Wire icing thickness prediction model of transmission line in the northeastern slope region of Qinghai-Xizang Plateau based on random forest algorithm

LYU Meixia^,, YAN Xinyang, HE Jinmei^,, CHENG Peng, WANG Xiaoyong, LI Xiaoqin

Meteorological Service Center of Gansu Province， Lanzhou 730020， China

通讯作者: 何金梅（1977—），女，甘肃兰州人，正高级工程师，主要从事专业气象预报服务工作。E-mail：441916974@qq.com。

责任编辑: 王涓力；校对：邓祖琴

收稿日期: 2024-05-14 修回日期: 2025-04-1

基金资助:

甘肃省自然科学基金项目(23JRRA1574)
甘肃省青年科技基金计划(24JRRA1186)
及甘肃省气象局重点项目(Zd2022-04)

Received: 2024-05-14 Revised: 2025-04-1

作者简介 About authors

吕玫霞（1995—），女，甘肃武威人，硕士，主要从事专业气象预报服务工作。E-mail：957985776@qq.com。

摘要

电线覆冰是危害青藏高原东北边坡地区输电线路安全运行的重要因素之一，研究区域内输电线路覆冰时空变化特征，建立覆冰预报模型，对电力部门融冰除冰及冰害防御有重要意义。基于随机森林算法，利用电力部门提供的2019－2022年青藏高原东北边坡地区输电线路覆冰个例，结合覆冰个例沿线气象实况监测资料，训练出最大等值覆冰厚度与气象要素间相关性的回归模型，并对模型进行评价。结果表明：覆冰线路主要分布在甘南高原、陇中高原、陇东高原及陇南山区地带，冬季覆冰事件频发；通过调整随机森林回归模型决策树的棵数、特征个数及最小叶子数可以有效提高模型预测精度；相对湿度、过去24 h降水量对各地理分区导线覆冰有较大影响；随机森林训练出的分区域输电线路最大等值覆冰厚度模型训练集平均绝对误差均小于2.8 mm，决定系数R²>0.7。随机森林模型能够预测青藏高原东北边坡地区输电线路最大等值覆冰厚度，可实现输电线路覆冰的短期预报。

关键词： 输电线路覆冰; 时空变化; 随机森林; 预报效果评估

Abstract

Wire icing is one of the important factors endangering the safe operation of power grid in northeastern slope region of Qinghai-Xizang Plateau. It is of great significance to study the temporal and spatial variation characteristics of transmission line icing and establish the icing forecasting model for the power department to remove ice and prevent ice damage. Based on the random forest algorithm, a regression model of the correlation between maximum equivalent ice thickness and meteorological elements was trained by using the cases of transmission line icing in northeastern slope region of Qinghai-Xizang Plateau from 2019 to 2022 provided by the power department, combined with the meteorological monitoring data along the icing cases, and the model was evaluated. The results show that transmission line icing accidents are mainly distributed in Gannan Plateau, Plateau of middle Gansu, Plateau of eastern Gansu, and Longnan mountainous area, and icing accidents occurred frequently in winter. The number of trees and features and the minimum number of leaves in the decision tree of the random forest regression model were adjusted to improve the prediction accuracy of the model. The relative humidity and the precipitation in the past 24 hours have great influence on transmission line icing in each geographical area. The mean absolute errors of the training set of maximum equivalent ice thickness prediction model of transmission line trained by random forest are all less than 2.8 mm, and the coefficient of determination R² is above 0.7. Therefore, the random forest model can predict the maximum equivalent ice thickness of transmission lines in the northeastern slope region of Qinghai-Xizang Plateau and realize short-term forecast, reduce the economic loss caused by transmission line icing in power grid.

Keywords： transmission line icing; temporal and spatial change characteristics; random forest; evaluation of prediction result

PDF (6976KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

吕玫霞, 闫昕旸, 何金梅, 程鹏, 王小勇, 李晓琴. 基于随机森林算法的青藏高原东北边坡输电线路覆冰厚度预报模型[J]. 干旱气象, 2025, 43(3): 488-497 DOI:10.11755/j.issn.1006-7639-2025-03-0488

LYU Meixia, YAN Xinyang, HE Jinmei, CHENG Peng, WANG Xiaoyong, LI Xiaoqin. Wire icing thickness prediction model of transmission line in the northeastern slope region of Qinghai-Xizang Plateau based on random forest algorithm[J]. Arid Meteorology, 2025, 43(3): 488-497 DOI:10.11755/j.issn.1006-7639-2025-03-0488

0 引言

输电线路覆冰是指气温低于0 ℃时，冷雾、冻雨或湿雪冻结在输电线路上的一种现象（Kringlebotn Nygaard et al.， 2013），它会引发线路跳闸、导线舞动、过荷载、覆冰闪络等电气事故，严重情况下甚至可导致倒塔断线、电网解列、绝缘子闪络等现象（Niu et al.，2012；王传辉等，2019），严重损坏电力设备，危害国民经济。青藏高原东北边坡地形复杂，山地起伏，沟壑纵横，密集的输电线路在跨越山区时受地形导致的局地小气候影响较大（李清华等，2022），运行条件极为恶劣，该区域电线覆冰一直是危害电网安全运行的重要因素之一。近年来甘肃河东冬季降雪及极端寒冷天气呈增加趋势（赵一飞等，2013），更是加大了输电线路覆冰的频率（Cohen et al.，2018）。因此，研究区域输电线路覆冰时空变化特征，建立更加准确的覆冰预报模型，为电力部门提前采取防冰除冰措施提供科学依据，无疑具有极大的科学价值与现实意义。

影响覆冰厚度的气象因素主要有降水、温度、湿度、风速等（赵晓萌等，2011；朱君等，2011；胡艳楠等，2017；覃武等，2019）。目前覆冰预报模型大致可以分为物理学预报模型与统计学预报模型。物理学覆冰预报模型或者通过热力学、流体力学原理建立守恒方程，从微观层面将覆冰重量同各类气象要素建立联系（朱永灿等，2015），或者综合考虑雾凇和雨凇以及热力学原理，建立输电线路覆冰模型（邓芳萍等，2017）。物理模型能很好地模拟电线积冰增长情况，预测标准冰厚的时空增长过程，模拟时空分辨率较高，但由于覆冰形成的微物理过程十分复杂，建模时对实际物理过程的简化，以及模型中如液滴撞击速度等重要参数无法准确测量，导致此类模型在实际业务工作中很少应用（Li et al.，2014）。传统的统计学预报模型基于温度、气压、风速、风向和相对湿度等气象要素，与输电线路覆冰厚度做简单的线性拟合。该方法依赖于大量历史资料，操作简便，可以较快得到电线覆冰规律（温华洋等，2011；王奇等，2021），但模型泛化能力较弱，全局预测能力不强（Hao et al.，2019）。而基于机器学习方法所建立的统计学模型则表现出较高的预报准确率（Sun and Wang，2019），使用机器学习方法建立的多种覆冰预报模型，取得了很好的应用效果（Niu et al.，2017；林刚等，2018；Zhao et al.，2022）。目前可建立不同电线绝缘子仿真物理模型，实现绝缘子覆冰情况下冰层厚度及冰棱长度模拟（赵多青等，2022）；还可融合Ridge及XGBoost等多种机器学习算法，学习历史时间序列下气象因子与覆冰厚度的相关性，结合WRF模式预报，实现覆冰预测（李晨曦，2023）；另外考虑微地形因素结合CALMET模式，实现复杂地形下导线覆冰的数值模拟（王帅等，2024）。

目前，甘肃省针对具体线路的精细化覆冰预报模型研究工作尚未开展，与电力部门的迫切需求形成鲜明对比。本文利用甘肃省电力部门提供的2019—2022年青藏高原东北边坡地区共计14个覆冰个例及覆冰发生时段各气象监测站点资料，分析覆冰的时空变化特征，基于机器学习中的随机森林方法分区域建立输电线路覆冰预报模型，并检验模型的预报性能，以期为今后开展输电线路覆冰专项预报提供技术支撑，为甘肃电网减少覆冰带来的经济损失，实现“双碳”目标保驾护航。

1 研究区概况

青藏高原东北边坡地区包括甘肃省河东地区以及宁夏固原地区，区域内地形复杂、地貌多样，横跨青藏高原及黄土高原（王莺等，2014），地形多为高原、山地及丘陵。区域内的特高压线路包括±1 100 kV吉泉线，±800 kV天中线、±800 kV祁韶线、±800 kV青豫线等，线路总长度超过3 000 km。按照覆冰区域内气候背景、地貌特征及输电线路分布，分陇南（Ⅰ区）、定西—天水（Ⅱ区）、甘南—临夏（Ⅲ区）、平凉—固原（Ⅳ区）、兰州—白银（Ⅴ区）等5个区域（图1）建立最大等值覆冰厚度预报模型，并选取覆冰个例杆塔附近15 km内气象站为代表性站点。

图1

新窗口打开| 下载原图ZIP| 生成PPT

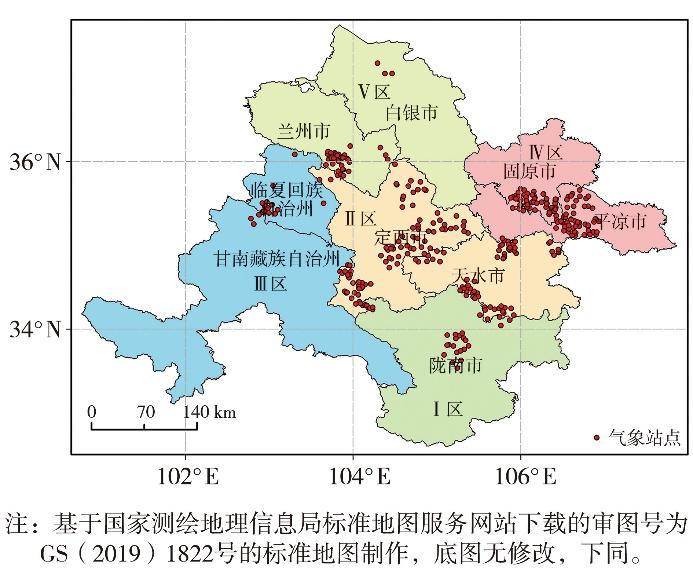
图1 覆冰区域及气象站点空间分布

Fig.1 Spatial distribution of transmission line icing region and meteorological stations

2 资料和方法

2.1 资料

输电线路覆冰资料为甘肃省电力部门提供的2019年11月—2022年1月青藏高原东北边坡地区共计14个覆冰个例，包含个例发生时间、天气现象、地理位置、覆冰持续时间、覆冰形态、最大等值覆冰厚度等信息。

综合以往研究成果（赵晓萌等，2011；吴息等，2012；胡艳楠等，2017；王馨等，2020），建模时用到的自变量包括10.5 m高度10 min平均风速（V₁₀），1.5 m高度气温（T）、最高气温（T_max）、最低气温（T_min），以及相对湿度（RH）和覆冰个例所在县区内对应国家站过去24 h降水量（R₂₄），所有数据均经过严格的质量控制，通过界限值检查、时间一致性及空间一致性检查。

随机森林模型的因变量为覆冰个例出现时间段内的最大等值覆冰厚度。本研究共收集到8 063个有效样本，按照5个地理分区境内输电线路分别建立模型，建模时随机打乱所有样本，按照4∶1的分段抽样比例生成训练集和测试集。表1为5个地区训练集和测试集样本数。

表1 研究区域训练集和测试集样本数

Tab.1 The number of training set and test set samples in the study area

样本	Ⅰ区	Ⅱ区	Ⅲ区	Ⅳ区	Ⅴ区
训练集	635	2 923	790	1 883	218
测试集	159	731	198	471	55

新窗口打开| 下载CSV

2.2 随机森林算法及模型构建

随机森林算法（Random Forest，RF）基于集成学习理论，使用Bootstrap抽样方式，通过构建多棵决策树形成森林，较好地解决了单个决策树容易出现过拟合的问题，学习速度较快，在处理离散变量及非线性回归问题方面有着出色表现，与传统的支持向量机等方法相比，RF具有准确率高、适应性强的特点（刘新伟等，2021）。

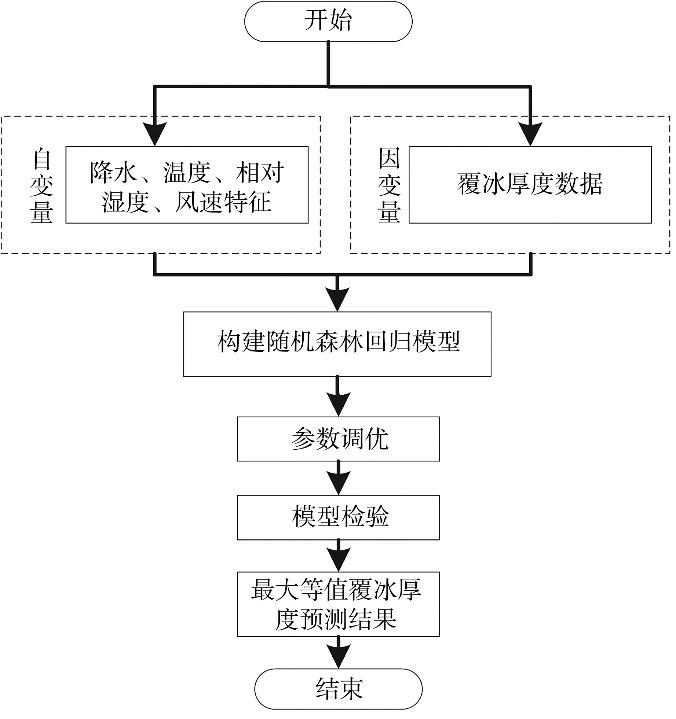
随机森林回归算法示意图见图2，本文构建的随机森林回归模型流程如图3所示。第1步使用覆冰个例发生时段内气温、降水、湿度、风速等6个气象因子作为模型输入，最大等值覆冰厚度作为模型输出，建立样本训练集。第2步样本训练首先针对数据分布不均匀的情况，使用Randperm方法打乱总样本数，解决类别不平衡问题；其次随机抽取出覆冰记录观测数据中的20%作为回归模型的测试数据，将剩余数据作为训练数据，由于各类特征数据间的差异性，将训练集与测试集进行归一化处理；然后使用Bootstrap抽样方式随机抽取n个样本数据集，未被抽取的剩余样本形成袋外数据（Out of Bag， OOB）（Rahman et al.，2006）。第3步随机抽取每个样本子集特征，按照最优特征子空间方法生成回归决策子树，每棵树不进行剪枝，将生成的决策子树建立随机森林（沈润平等，2017）。第4步对生成的RF模型进行参数调优及模型检验，生成最终预测结果。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 随机森林回归算法示意图

Fig.2 Schematic map of the random forest regression algorithm

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 随机森林回归模型构建流程图

Fig.3 Flow chart of the random forest regression model construction

使用平均袋外误差 $\bar{O O B}$ 进行参数调优（王可心等，2021），其公式为

（1）

\bar{O O B} = \frac{1}{N_{t r e e}} \sum_{i - 1}^{N_{t r e e}} O O B_{i}

（2）

O O B_{i} = \frac{1}{m} \sum_{j - 1}^{m} (y_{j} - {\hat{y}}_{j})^{2}

式中：N_tree为随机森林中决策树的棵数，i为回归树的序号，m为袋外样本个数，j为袋外样本编号，OOB_i为第i个回归树的袋外误差，y_j为袋外样本真实值， ${\hat{y}}_{j}$ 为袋外样本预测值。

2.3 模型评估指标

使用平均绝对误差（Mean Absolute Error， MAE）、平均偏差误差（Mean Bias Error， MBE）、决定系数（R²）、均方根误差（Root Mean Square Error， RMSE）进行模型的检验（王可心等，2021），计算公式分别为

（3）

M A E = \frac{1}{n} \sum_{i = 1}^{n} |{\hat{y}}_{i} - y_{i}|

（4）

M B E = \frac{1}{n} \sum_{i = 1}^{n} ({\hat{y}}_{i} - y_{i})

（5）

R^{2} = 1 - \frac{\sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})^{2}}{\sum_{i = 1}^{n} (y_{i} {- \bar{y})}^{2}}

（6）RMSE=

\sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}

式中：y_i为因变量真实值， ${\hat{y}}_{i}$ 为因变量预测值， $\bar{y}$ 为因变量真实值的平均值，n为样本数量，i为样本序号。

计算特征变量因子的重要性评分（Variable Importance Measure， VIM），评分越高代表该变量因子重要程度越高，对因变量的影响程度越高，即回归模型解释程度越高（Groemping，2009）。VIM通过决策树平均袋外误差变化评估特征因子重要程度。首先计算m个袋外数据（OOB）的均方误差（Mean Square Error， MSE），为MSE₁，MSE₂，…，MSE_m，其次随机置换m个OOB数据集特征分裂时选择的特征，形成新的OOB并计算MSE，重复M次，M为自变量的个数，使用随机置换后的OOB均方误差建立如下矩阵：

（7）

\begin{array}{l} [\begin{matrix} M S E_{11} & M S E_{12} & \dots & M S E_{1 m} \\ M S E_{21} & M S E_{22} & \dots & M S E_{2 m} \\ ⋮ & ⋱ & M S E_{i j} & ⋮ \\ M S E_{M 1} & M S E_{M 2} & \dots & M S E_{M m} \end{matrix}] \\ (1 \leq i \leq M, 1 \leq j \leq m) \end{array}

最后计算第i个特征变量因子的VIM，公式（杨明悦和毛献忠，2022）如下：

（8）

E_{S} = \sqrt{\frac{\sum_{i = 1}^{M} M S E_{i j} - \bar{M S E_{j}}}{M - 1}}

（9）

V I M_{i} (M S E) = (\frac{1}{m} \sum_{j = 1}^{m} (M S E_{j} - M S E_{i j})) / E_{S}

式中：E_S代表标准误差，VIM_i（MSE）代表第i个特征变量因子的重要性评分。

采用命中率（Probability Of Detection，POD）、空报率（False Alarm Rate，FAR）、漏报率（Missing Alarm Rate，MAR）评估模型拟合效果（唐文苑等，2017）。

2.4 参数调优

影响RF模型预测能力的3个重要可变参数为决策树的棵数N_tree、特征分裂时选择的特征个数f以及最小叶子数L_min。一般情况下f取值为 $\sqrt{M} / 2$ 、M/3、log₂M、M，其中M为原始数据集中自变量个数，即为6。

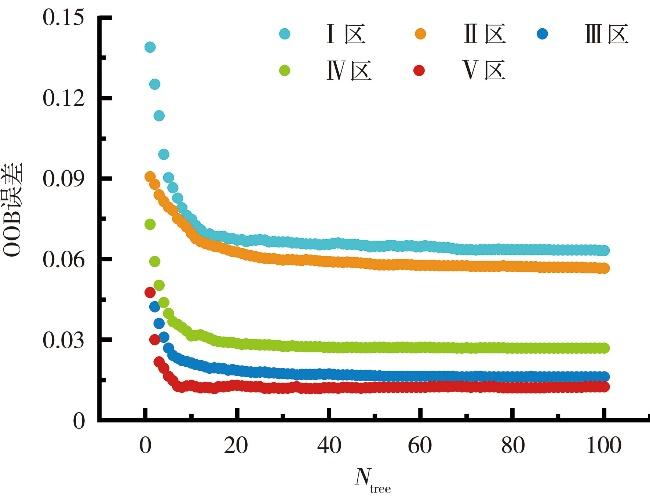
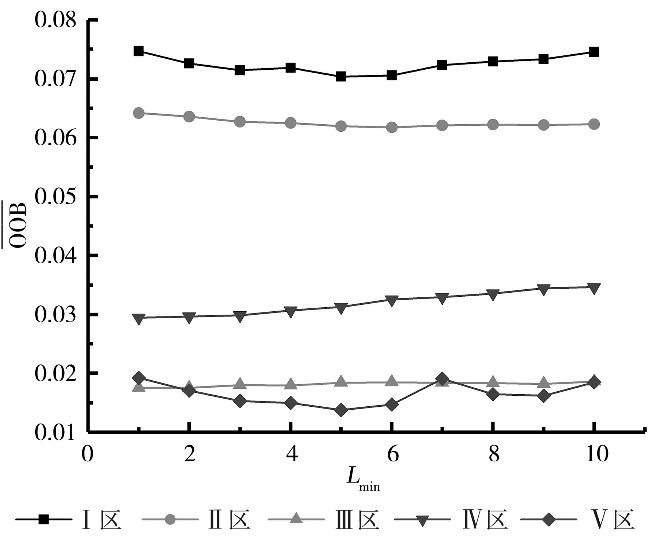
1）默认N_tree最大为100，L_min为5，然后分别观察5个地理分区建立100棵决策子树的 $\bar{O O B}$ 随f的变化趋势，为保证每次随机采样结果一致，固定设置随机数生成器的种子来确保每次回归得到相同结果。随着N_tree的增大，各区当f=M=6时曲线误差最小， $\bar{O O B}$ 最低，因此确定f=6。

2）固定L_min为5，当f=6时观察OOB误差随N_tree的变化（图4）。可以看到，随着N_tree增加，OOB误差逐渐趋于平稳。通常认为当OOB误差维持稳定时，决策树数目为最优。观察各区OOB误差变化情况，I区误差总体最高，决策树迭代70次以后，误差稳定在0.063左右；II区误差次高，决策树迭代80次以后，决策树误差稳定在0.057左右；IV区，决策树迭代50次以后，误差稳定在0.027左右；III区误差较低，决策树迭代90次以后，误差稳定在0.016左右；V区决策树迭代50次以后，误差稳定在0.012左右。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 5个区域OOB误差与N_tree关系（L_min=5， f=6）

Fig.4 The relationship between OOB errorand N_tree in five zones （L_min=5 and f=6）

综合考虑5个区域OOB误差趋势，当决策树数目超过50以后，误差曲线下降趋势缓慢，趋于平稳，模型过拟合，增加决策树数量对减少误差效果不明显。因此Ⅰ~Ⅴ区选择决策树数目分别为70、80、90、50、50。

图5为不同区域 $\bar{O O B}$ 随L_min的变化趋势。Ⅰ区， $\bar{O O B}$ 在L_min=5时达到最低，然后迅速上升；Ⅱ区， $\bar{O O B}$ 在L_min=6时最低，然后缓慢上升；Ⅲ区， $\bar{O O B}$ 随L_min的增多呈震荡上升趋势；Ⅳ区， $\bar{O O B}$ 呈平缓上升趋势；Ⅴ区， $\bar{O O B}$ 在L_min=5时达到最低。最终各区域模型参数调优结果见表2。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 The relationship between $\bar{O O B}$ and L_min in five zones

Fig.5

表2 各区域模型参数调优结果

Tab.2 The results of model parameter tuning for each zone

区域	N_tree	f	L_min
I区	70	6	5
II区	80	6	6
III区	90	6	2
IV区	50	6	1
V区	50	6	5

新窗口打开| 下载CSV

3 结果分析

3.1 输电线路覆冰灾害时空变化

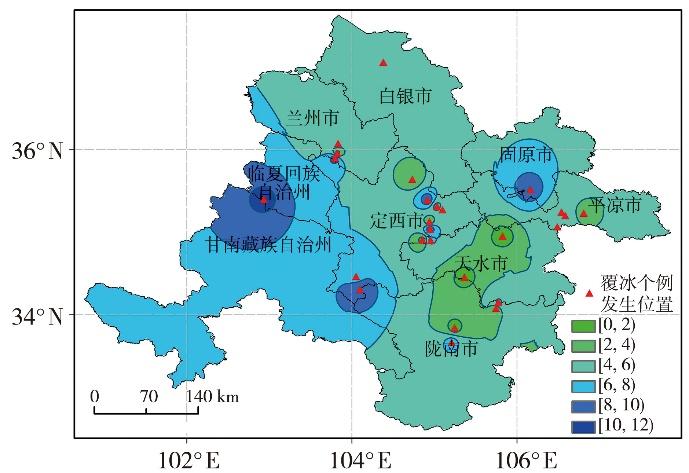
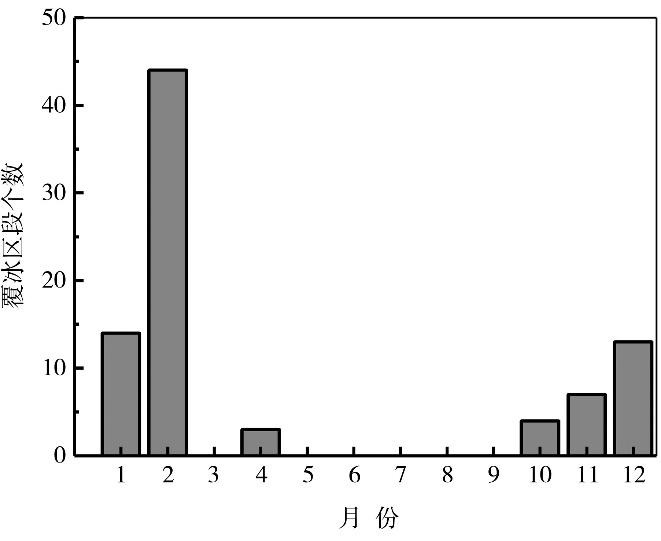
2019—2022年14个输电线路覆冰个例共计72个电线区段发生覆冰。其中，Ⅱ区覆冰区段最多（34个），定西市24个区段发生覆冰，主要发生在定西东部通渭县，天水市10个，主要发生在秦州区、秦安县及武山县；Ⅳ区覆冰区段次多，为23个，主要发生在平凉中部华亭市、崆峒区及宁夏固原市；Ⅴ区、Ⅰ区、Ⅲ区分别出现7、6、2个覆冰区段，覆冰主要发生在兰州南部七里河区、陇南中部武都区及甘南州北部夏河县。Ⅲ区及固原南部最大等值覆冰厚度最大，为10 mm及以上，陇南北部、天水中部、定西北部及平凉东部最大等值覆冰厚度为4 mm及以下，其余地区最大等值覆冰厚度为4~10 mm（图6）。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 2019－2022年输电线路覆冰个例位置分布及最大等值覆冰厚度（单位：mm）插值

Fig.6 Distribution of transmission line icing cases position and interpolation of maximum equivalent ice thickness （Unit： mm） during 2019-2022

从输电线路覆冰区段个数月变化（图7）可见，覆冰主要发生在冬季11月至次年2月，其中2月覆冰区段最多（44个），1月、12月次多，分别为14、13个覆冰区段，这与我国其他地区的研究结论较为一致（黄新波等，2008）。一般而言，当气温在-20 ℃与0 ℃之间时，气温越高，覆冰速率越快，气温为-5~-1 ℃时，最容易形成覆冰（刘春城和刘佼，2011）。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 2019—2022年输电线路覆冰区段个数月变化

Fig.7 Monthly variation of number of the transmission line icing section from 2019 to 2022

3.2 模型评价及检验

3.2.1 模型评价

通过多次交叉验证，选取最优值得出5个区域输电线路最大等值覆冰厚度预报模型的MAE、MBE、R²、RMSE评价结果如表3所示。各区域训练集平均绝对误差均小于2.8 mm，决定系数R²>0.7。Ⅲ区MAE、MBE及RMSE最高，其次为Ⅱ区和Ⅰ区，Ⅳ区及Ⅴ区的误差较小，MAE、MBE均小于0.950 mm，RMSE均小于1.680 mm，说明Ⅳ区及Ⅴ区模型预测偏差较小，预估能力较好。Ⅰ区、Ⅲ区、Ⅳ区及Ⅴ区训练集R²都在0.840以上，测试集R²在0.690以上，其中Ⅳ区及Ⅴ区训练集R²在0.913与0.960之间，测试集R²在0.765与0.841之间，代表Ⅳ区及Ⅴ区模型拟合效果较好，对最大等值覆冰厚度解释程度较强，具备较好的泛化能力。综合对比分析得到，Ⅳ区及Ⅴ区模型预测性能较优，预测结果较为理想；Ⅰ区模型预测精度较高，模型拟合优度较高；Ⅲ区模型自变量对因变量的解释能力较强；Ⅱ区训练集R²为0.701，模型自变量对最大等值覆冰厚度的解释能力尚可。

表3 输电线路最大等值覆冰厚度预报模型评价结果

Tab.3 Evaluation results of maximum equivalent ice cover thickness prediction model for transmission lines

区域	MAE/mm		MBE/mm		R²		RMSE/mm
区域	训练集	测试集	训练集	测试集	训练集	测试集	训练集	测试集
Ⅰ区	1.048	1.387	-0.001	-0.064	0.842	0.695	1.558	2.117
Ⅱ区	1.326	1.962	-0.003	-0.184	0.701	0.409	1.827	2.633
Ⅲ区	1.438	2.765	0.023	0.660	0.945	0.857	2.883	4.833
Ⅳ区	0.379	0.947	0.003	0.014	0.960	0.765	0.707	1.670
Ⅴ区	0.259	0.420	0.009	0.038	0.913	0.841	0.995	1.266

新窗口打开| 下载CSV

3.2.2 拟合效果

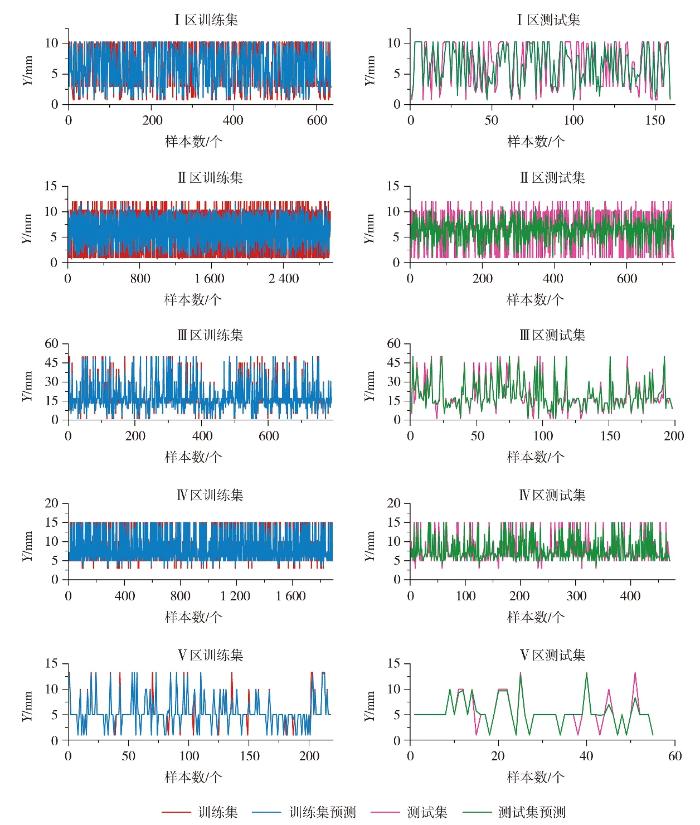
表4为输电线路最大等值覆冰厚度（Y）模型拟合效果评估，划分Y所属类别范围时参考《中重冰区架空输电线路设计技术规定》（国家电网有限公司，2024），其中除III区外，其余各区均不存在Y≥20 mm的样本；图8为5个区域输电线路最大等值覆冰厚度Y预测结果与真实值对比。综合可以看到，对于I区，模型训练集预测结果与真实值变化趋同，但10<Y<20 mm时存在漏报；Y≤10 mm时存在空报。对于II区，对Y≤10 mm样本，模型命中率（POD）较高，预测结果较好，存在少量漏报和空报情况；对10<Y<20 mm样本，模型POD较低，存在较高的漏报情况。对于III区，训练集、测试集与真实值拟合精度均较高，对Y≤10 mm样本，训练集没有漏报情况；对10<Y<20 mm样本，训练集没有空报情况；对Y≥20 mm样本，训练集与测试集均无漏报情况。对于IV区，对Y≤10 mm样本，POD超过0.896，拟合效果较好；对10<Y<20 mm样本，模型存在一定的空报情况。对于V区，训练集与测试集预测结果均较好，POD均达到0.667以上，测试集对Y≤10 mm样本的漏报率与10<Y<20 mm样本的空报率均为0。

表4 输电线路最大等值覆冰厚度（Y）模型拟合效果评估

Tab.4 Evaluation of model fitting effect of maximum equivalent ice thickness （Y） for transmission lines

区域	样本集	POD			FAR			MAR
区域	样本集	Y≤10 mm	10<Y<20 mm	Y≥20 mm	Y≤10 mm	10<Y<20 mm	Y≥20 mm	Y≤10 mm	10<Y<20 mm	Y≥20 mm
Ⅰ区	训练集	0.794	0.545	/	0.206	0	/	0	0.455	/
Ⅰ区	测试集	0.783	0.600	/	0.217	0	/	0	0.400	/
Ⅱ区	训练集	0.858	0.136	/	0.133	0.319	/	0.012	0.854	/
Ⅱ区	测试集	0.834	0.098	/	0.158	0.350	/	0.012	0.896	/
Ⅲ区	训练集	0.859	0.913	0.883	0.141	0	0.117	0	0.087	0
Ⅲ区	测试集	0.775	0.810	0.797	0.184	0.021	0.203	0.061	0.175	0
Ⅳ区	训练集	0.946	0.791	/	0.001	0.207	/	0.054	0.003	/
Ⅳ区	测试集	0.896	0.611	/	0.019	0.347	/	0.088	0.096	/
Ⅴ区	训练集	0.980	0.818	/	0.015	0.053	/	0.005	0.143	/
Ⅴ区	测试集	0.981	0.667	/	0.019	0	/	0	0.333	/

注：“/”表示无样本。

新窗口打开| 下载CSV

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 5个区域输电线路最大等值覆冰厚度（Y）模型预测结果与真实值对比

Fig.8 Comparison between the model prediction results of the maximum equivalent ice cover thickness （Y） and the real value of transmission lines in 5 zones

综合来看，II区、IV区及V区对10<Y<20 mm样本模型命中率均较高，预测结果与真实值拟合程度较好；III区及V区对10<Y<20 mm样本的命中率较高，且III区对Y≥20 mm样本的命中率较高，无漏报情况；II区对10<Y<20 mm样本漏报情况较多，其余各区预测结果漏报及空报情况均较少。

4 覆冰事件与气象因子的关系

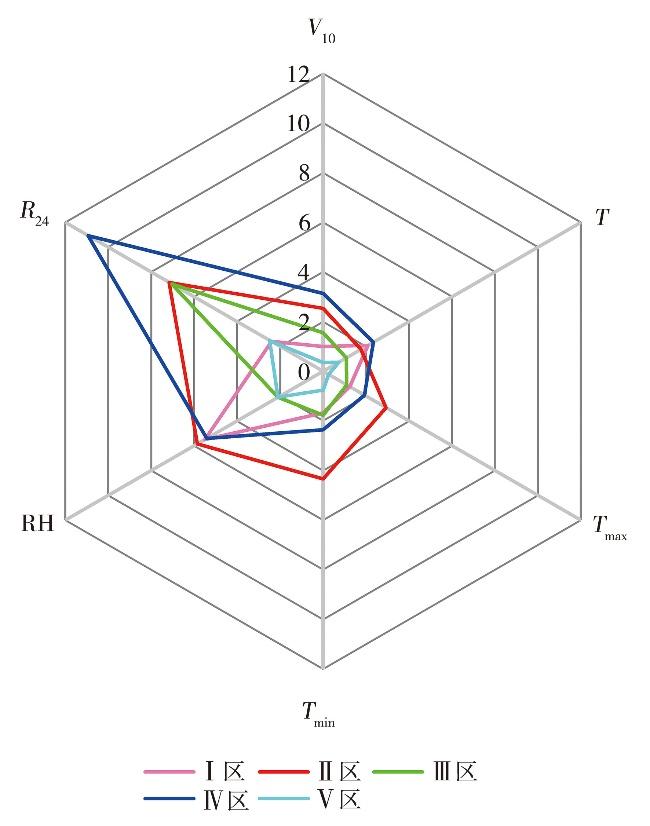
V₁₀、T、T_max、T_min、RH以及R₂₄是反映输电线路覆冰程度的重要指标（黄新波等，2011），图9为5个区域6个气象因子的VIM特征图。可以看到，Ⅰ区RH重要性评分最高，接近于R₂₄和T评分的2倍；Ⅰ区属于半干旱半湿润区，研究个例中输电线路出现雾凇的情况较多，而雾凇覆冰过程多为干增长（孙才新等，2003）。II区R₂₄重要性评分排名最高，RH和T_min次之；Ⅱ区个例覆冰过程多为混合冻结冰壳，雾雨凇交替在电线上积聚，这类混合凇覆冰增长过程介于干增长和湿增长之间（苑吉河等，2004），混合凇周期较长，空气湿度较大，存在足够多的过冷却水滴（黄筱婷等，2013），这与该区域覆冰个例前期降水带来充足水汽，雨凇和雾凇混合冻结附着在导线上，形成覆冰的情况较吻合。III区R₂₄重要性评分远大于其他因子；该区域个例覆冰过程主要为雾凇，经电力部门观测，等值覆冰厚度随降雪天气持续而逐渐增长。Ⅳ区R₂₄重要性评分接近于其他因子之和；该区域个例导线覆冰以雪凇、雾凇较多，雾凇最大附着厚度为70 mm。V区R₂₄与RH因子重要性评分相当，对导线覆冰有较大影响；该区域导线覆冰主要为雾凇及混合凇，覆冰过程存在干增长及湿增长过程，降雪过程带来水汽，水蒸气凝华或冻结在导线易形成覆冰，另一方面空气湿度较高，水汽量处于过饱和状态，过冷却水滴易形成混合凇（彭曙蓉等，2016）。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 5个区域气象因子的VIM特征图

Fig.9 The VIM map of meteorological factors in five zones

综合来看，所有分区的R₂₄、RH对输电线路覆冰的影响最大，T_min对Ⅱ、Ⅲ、Ⅴ区的影响、T对Ⅰ区的影响以及V₁₀对Ⅳ区的影响同样不可忽视，这也是实际预报服务业务中需要关注的重点。

5 结论

本文利用甘肃省电力部门提供的2019—2022年青藏高原东北边坡地区共计14个覆冰个例，分析了覆冰的时空变化特征，基于机器学习中的随机森林算法分区域建立了输电线路覆冰预报模型，得到以下主要结论。

1）青藏高原东北边坡地区覆冰线路主要分布在甘南高原、陇中高原、陇东高原及陇南山区地带，定西、天水地区覆冰频次最多，甘南、临夏及固原地区最大等值覆冰厚度较大，覆冰出现时段主要分布在冬季12月至次年2月，其中2月出现的覆冰区段最多。

2）基于RF回归模型可以有效预测输电线路最大等值覆冰厚度，通过调整决策树棵数、特征分裂时选择的特征个数以及最小叶子数可以改变模型的拟合效果，提高模型预测精度，更好地解释最大等值覆冰厚度。

3）各模型预测结果与真实值变化形势趋同，Ⅳ区及Ⅴ区训练集R²均大于或等于0.913，测试集R²均大于或等于0.765，MAE、MBE及RMSE较小，模型拟合效果较好，对最大等值覆冰厚度解释程度较强，具备较好的泛化能力；Ⅰ区模型预测精度较高，模型拟合优度较高；Ⅲ区模型自变量对因变量的解释能力较强；Ⅱ区训练集R²为0.701，模型自变量对最大等值覆冰厚度的解释能力尚可。总体来看，各区域模型预测结果准确率较高，误差较低，可用于实际最大等值覆冰厚度预测业务中。

输电线路覆冰往往出现在高海拔山区，受局地气候影响明显，观测资料匮乏，这也是覆冰预报的难点。本文在有限资料的基础上，通过多次交叉试验，调整关键因子的取值，在最大等值覆冰厚度预报模型上进行了初步探索，但仍存在一定的不足，比如覆冰样本量较少、气象监测因子不足等。随着2024年甘肃省15套输电线路覆冰在线监测设备的投入使用，覆冰样本及气象监测因子的不断积累，模型的性能将逐步优化，进一步提高其预警和预报能力。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

邓芳萍, 康丽莉, 姜瑜君, 等, 2017.

基于常规气象资料的小时标准冰厚模型及验证

[J]. 应用气象学报, 28(2): 142-156.