西宁市短历时暴雨雨型及重现期极值降水特征研究

doi:10.11755/j.issn.1006-7639-2025-01-0153

西宁市短历时暴雨雨型及重现期极值降水特征研究

王紫文^,¹, 赵海涵², 余迪^,¹, 汪洋³, 陶世银¹, 李万志¹

1.青海省气候中心，青海西宁 810001

2.青海大学农牧学院，青海西宁 810016

3.兰州大学大气科学学院，甘肃兰州 730000

Study on the temporal patterns and extreme precipitation characteristics of short-duration torrential rain in Xining city

WANG Ziwen^,¹, ZHAO Haihan², YU Di^,¹, WANG Yang³, TAO Shiyin¹, LI Wanzhi¹

1. Qinghai Climate Center，Xining 810001，China

2. College of Agriculture and Animal Husbandry，Qinghai University，Xining 810016，China

3. College of Atmospheric Sciences，Lanzhou University，Lanzhou 730000，China

通讯作者: 余迪（1992—），女，陕西眉县人，工程师，主要从事气象灾害风险研究。E-mail：52400282@qq.com。

责任编辑: 邓祖琴；校对：王涓力

收稿日期: 2024-09-27 修回日期: 2024-11-1

基金资助:

第二次青藏高原综合科学考察研究项目(2019QZKK0906)
青海省气象局面上科研项目(QXMS2023-36)

Received: 2024-09-27 Revised: 2024-11-1

作者简介 About authors

王紫文（1993—），男，青海西宁人，工程师，主要从事气候应用与气候可行性论证技术研究。E-mail：ziwenw@foxmail.com。

摘要

暴雨雨型和极端强降水重现期是城市应对暴雨洪涝灾害的重要气象参数。利用西宁市国家基本气象站近60 a逐分钟降水资料，采用模糊识别法和数理统计法对西宁市暴雨过程进行雨型分类和特征分析，并利用耿贝尔分布、皮尔逊Ⅲ型分布和广义极值分布对11种不同历时年最大降雨极值的概率分布进行拟合，评价拟合优度，并推算各历时降雨极值重现期。结果表明：1954—2022年西宁市共出现暴雨95场，过程累计雨量为25~40 mm，暴雨日数年际差异较大，整体呈增加趋势。暴雨雨型以单峰型为主，占总暴雨场次的85.3%，主要出现在7—9月。单峰雨型中，峰值多位于降水过程的前中期；雨量高值时段为20：00—次日09：00，高频率时段为23：00—次日09：00，两者并未完全重合。不同历时降雨极值的概率分布均较好地服从耿贝尔分布、皮尔逊Ⅲ型分布和广义极值分布，其中皮尔逊Ⅲ型分布的拟合精度最高。Ⅰ类雨型中小时降雨量最大达43.7 mm，超过100 a一遇的水平，Ⅱ类雨型的最大小时降雨量达38.1 mm，超过50 a一遇水平，Ⅴ类雨型的最大小时降雨量接近20 a一遇水平，其他雨型的最大小时降雨量在2 a一遇到10 a一遇水平。通过确定西宁市暴雨雨型和雨量极值的重现期，可以为城市内涝防治和室外排水设计提供科学依据。

关键词： 西宁; 暴雨雨型; 短历时降雨; 重现期

Abstract

Rainstorm patterns and extreme rainfall return periods are important meteorological parameters for cities response to rainstorm and flood disasters. Based on the 60-year minute-by-minute precipitation data from the national meteorological stations in Xining, the fuzzy recognition method and statistical analysis were used to classify and analyze the characteristics of rainfall processes in Xining. The Gumbel distribution, Pearson-III distribution, and generalized extreme value distribution were applied to fit the probability distributions of the annual maximum rainfall extremes for 11 different durations. The goodness of fit for each distribution was evaluated, and the return periods of rainfall extremes for each duration were estimated. The results show that, from 1954 to 2022, there were a total of 95 rainstorm events in Xining, with cumulative rainfall ranging from 25 to 40 mm. The number of rainstorm days showed significant interannual variation, with an overall increasing trend. The rainstorm pattern was predominantly unimodal, accounting for 85.3% of total rainstorm events, which mainly occurred from July to September. In the unimodal pattern, the peak rainfall was primarily concentrated in the early to mid-phase of the rainfall process. The high rainfall intensity occurred from 20:00 to 09:00 the following day, while the high-frequency rainfall periods were between 23:00 and 09:00 the following day, although these two periods did not fully coincide. The probability distributions of rainfall extreme values for different durations obeyed the Gumbel, Pearson-III, and generalized extreme value distributions well, and the Pearson type III distribution had the highest fitting accuracy. The maximum hourly rainfall for Type I events reached 43.7 mm, exceeding the 100-year return period; for Type II events, the maximum hourly rainfall was 38.1 mm, exceeding the 50-year return period; and for Type V events, the maximum hourly rainfall was close to 20.0 mm, approaching the 20-year return period. The maximum hourly rainfall for other patterns ranged from the 2-year to the 10-year return period. The identification of rainstorm patterns and extreme rainfall return periods in Xining can provide valuable scientific data for urban flood prevention and outdoor drainage system design.

Keywords： Xining; temporal pattern of torrential rain; short-duration heavy rainfall; return period

PDF (3688KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王紫文, 赵海涵, 余迪, 汪洋, 陶世银, 李万志. 西宁市短历时暴雨雨型及重现期极值降水特征研究[J]. 干旱气象, 2025, 43(1): 153-161 DOI:10.11755/j.issn.1006-7639-2025-01-0153

WANG Ziwen, ZHAO Haihan, YU Di, WANG Yang, TAO Shiyin, LI Wanzhi. Study on the temporal patterns and extreme precipitation characteristics of short-duration torrential rain in Xining city[J]. Arid Meteorology, 2025, 43(1): 153-161 DOI:10.11755/j.issn.1006-7639-2025-01-0153

0 引言

随着气候变化和城市化进程的加剧，城市暴雨洪涝灾害日益严重（Guan et al.，2016）。如2012年北京“7·21”特大暴雨（谌芸等，2012）和2021年郑州“7·20”特大暴雨（苏爱芳等，2021），均造成了重大生命财产损失。政府间气候变化专门委员会（IPCC）第六次评估报告（AR6）指出，气候变化已经对全球各地区的极端天气和气候事件产生了显著影响，并且未来持续增暖可能导致极端事件愈加频繁和严重。在此背景下，如何有效保障城市安全，减轻极端暴雨灾害的影响，成为当前城市建设的核心议题（焦胜等，2019；李会安等，2022）。

暴雨雨型展示了暴雨强度在不同降雨历时内的时间分配过程，即强度随时间的变化规律（严正宵等，2020）。研究表明，不同雨型产生的洪峰流量差异较大（吴彰春等，1995），因此在城市内涝防治和海绵城市建设中，不同雨型的雨水管网设计参数也不相同（张格，2023）。早在20世纪40年代，莫洛科夫和施果林（1956）通过对乌克兰地区降雨资料的统计分析，划分出7类雨型，并发现强度均匀的雨型较为稀少（岑国平等，1998）。Keifer和Chu（1957）根据强度、历时、频率关系提出了芝加哥设计雨型，随后Huff（1967）、Pilgrim和Cordery（1975）、Yen和Chow（1980）、Kibler（1982）等学者相继提出不同设计雨型。针对西宁市的暴雨雨型研究，何永晴等（2019）利用1954—2017年逐分钟降水数据推算了芝加哥设计雨型，结果显示西宁市短历时暴雨呈单峰特征，峰值多出现在降水初期。此外，相关研究（王彬雁等，2015；成丹和陈正洪，2017；袁冯等，2020；徐俊杰等，2023）基于逐分钟降水资料，通过不同分类方法对暴雨雨型的分类、年际变化及空间特征展开分析，为不同地区科学应对极端暴雨灾害提供了重要依据。

暴雨设计重现期的推算需选取合适的极值概率分布模型。由于降水的地区差异，目前尚无统一的模型适用于所有场景。常用的极值概率统计分析模型包括皮尔逊Ⅲ型分布、Weibull分布、耿贝尔分布等。Liu等（2024）在径流重现期计算中评估了多种概率分布方法，发现皮尔逊Ⅲ型分布、Logistic分布和Weibull分布拟合效果最佳；De Araújo Nunes等（2022）利用耿贝尔分布推算水库库容重现期以克服样本长度限制；Cho等（2023）结合广义极值分布与Copula函数对极值降雨深度及最大风速的联合重现期进行分析，识别飓风过程的极端性；国内在研究不同气象要素的极值概率分布及重现期推算中（邱译萱等，2021；李清华等，2022；杨扬等，2023），发现耿贝尔分布和广义极值分布的广泛适用性。

暴雨雨型与极端降水重现期是影响城市室外排水设计和内涝防治的重要气象参数，两者直接决定了内涝防治设计重现期和最大允许退水时间。其中，暴雨雨型对小流域的洪峰流量和流量过程有重要影响（吴彰春等，1995），而降雨重现期是雨水管渠设计重现期的重要依据。因此，掌握暴雨分型及不同历时降雨量极值的分布特征，并推算其重现期，对于城市防洪排水规划设计、海绵城市建设及气象防灾减灾具有重要意义（王彬雁等，2015；虞美秀等，2022；邓成等，2023；舒心怡等，2023）。

青海省西宁市位于湟水谷地，地形复杂，地表植被覆盖率低，水源涵养能力弱。暴雨、城市内涝及泥石流等灾害频发，严重影响了当地经济发展和人民生命财产安全。西宁市年平均降水量为415.4 mm，强降水主要集中在汛期（5—9月），占全年降水总量的86%，且以短历时强降雨为主。近年来，西宁市极端降水事件在频次和强度上呈增加趋势（张翠花等，2020；谢捷等，2022），极端降水引发的暴雨洪涝已成为当地受灾次数排名第二的气象灾害（李昌玉，2011）。因此，深入研究西宁市极端降水的雨型与极值特征，具有重要的科学与实践意义。

目前关于西宁市降水的研究多集中在气候暖湿化背景下的降水变化趋势及其引发的洪涝灾害方面，而针对设计暴雨雨型、降雨极值概率分布的模拟精度以及短历时降雨极值在不同雨型中的分布等方面的研究相对较少。此外，现有暴雨雨型研究主要集中于湿润半湿润地区，而对暴雨雨量较小、场次较少的干旱半干旱地区，雨型分类方法的适用性及极值分布拟合方法的研究较为缺乏。本文利用近60 a西宁市国家基本气象站逐分钟降雨资料，基于《气候可行性论证规范极值概率统计分析》（全国气候与气候变化标准化技术委员会，2019），使用耿贝尔分布、皮尔逊Ⅲ型分布和广义极值分布拟合西宁市不同历时降雨分布，并通过拟合优度评价极值拟合效果。结合模糊识别法划分暴雨雨型，探索适用于高原半干旱地区的降雨极值拟合方法，以期为西宁市的防洪排涝和防灾减灾提供科学依据。

1 资料与方法

1.1 资料来源

所用降水数据来自于西宁市国家基本气象站，该站位于西宁市城北区，降水观测数据连续完整，分钟数据序列较长。逐分钟降水资料的时间范围为1954—2001年和2011—2022年共60 a。其中，1954—2001年的数据由雨量自记纸降水曲线跟踪计算并经信息化处理；2011—2022年的数据为气象站自动记录的逐分钟雨量数据；2002—2010年无逐分钟降水观测记录。24 h（20：00—次日20：00，北京时，下同）日降水量数据的时间范围为1954—2022年，共69 a。以上数据均由青海省气象信息中心提供。

1.2 研究方法

1.2.1 暴雨判定及雨型划分

根据《气象灾害分级指标》（青海省气象局，2018），暴雨定义为20：00—次日20：00的1 440 min降雨量大于等于25.0 mm的降雨过程。采用模糊识别法（岑国平等，1998）对暴雨过程进行雨型划分，依据暴雨的时程分布特征判定其雨型类型。

每场降雨的时程特征不同，基于莫洛科夫和施果林（1956）提出的模式雨型理论，可将降雨过程划分为7类雨型（图1）。其中，Ⅰ、Ⅱ、Ⅲ型为单峰型降雨，分别为前期峰值型、后期峰值型和中期峰值型；Ⅳ型为均匀型降雨，降雨过程强度分布较均匀；Ⅴ、Ⅵ、Ⅶ型为双峰型降雨，分别为前后双峰型、前中双峰型和中后双峰型。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 7类暴雨雨型

Fig.1 Seven typical temporal patterns of rainstorm

依据《室外排水设计标准》（上海市政工程设计研究总院（集团）有限公司，2021），选取5、10、15、20、30、45、60、90、120、150、180 min共11个历时，以及2、5、10、50、100 a共5个重现期，以60 a逐分钟降水数据作为研究样本，采用年最大值法提取极值样本，利用耿贝尔分布、皮尔逊Ⅲ型分布和广义极值分布对样本频率分布进行拟合，计算各历时降水极值及其重现期。耿贝尔分布适用于模拟极端降水等极少见事件；皮尔逊Ⅲ型分布广泛应用于水文和气象领域，适合分析降水和流量等变量的概率分布；广义极值分布涵盖多种极值分布形式，适用于不同类型的极端气象变量。通过拟合优度评价对上述模型进行对比，选取适合西宁暴雨特点的最佳概率分布模型。

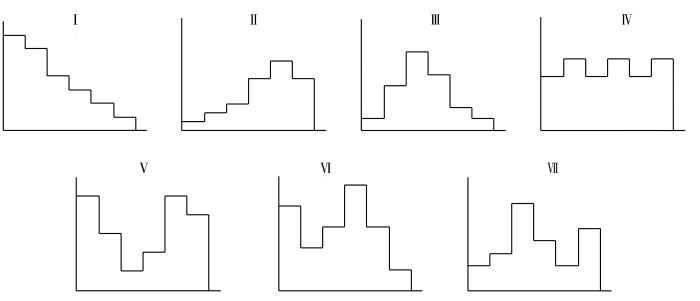
雨型识别是将每场实际发生的降雨归类为模式雨型中某一种类型的过程，通常采用目估法或模糊识别法（徐俊杰等，2023）。目估法通过人工判断每场降雨过程绘制的直方图来确定雨型，此方法操作简便，但易受主观因素影响，存在较大人为误差；模糊识别法将实际降雨的时程分配过程与模式雨型进行比较，计算实际降雨与各模式雨型的贴近度，以贴近度最大的模式雨型作为该场降雨的雨型。

本文采用模糊识别法（岑国平等，1998）对暴雨雨型进行识别。具体步骤：首先计算每时段雨量占总雨量的比例，将一场降雨划分为m个相等的时段，每个时段的雨量占总雨量的比例x_i为

（1）

x_{i} = P_{i} / P

(i = 1,2, \dots, m)

式中：P_i为每时段的降雨量，P为降雨过程的总雨量，单位均为mm。

将各时段的x_i作为该场降雨的雨型指标，用向量X表示，即

（2）

X = (x_{1}, x_{2}, \dots, x_{m})

同样，将7类模式雨型用向量形式表示为

（3）

V_{k} = (v_{k 1}, v_{k 2}, \dots, v_{k m})

(k = 1,2, \dots, 7)

式中：v_ki为模式雨型向量，V_k为7种模式雨型的向量矩阵，其分布矩阵为

（4）

V_{k} = [\begin{matrix} 7 / 23 & 6 / 23 & 4 / 23 & 3 / 23 & 2 / 23 & 1 / 23 \\ 1 / 26 & 2 / 26 & 3 / 26 & 6 / 26 & 8 / 26 & 6 / 26 \\ 1 / 20 & 4 / 20 & 7 / 20 & 5 / 20 & 2 / 20 & 1 / 20 \\ 3 / 21 & 4 / 21 & 3 / 21 & 4 / 21 & 3 / 21 & 4 / 21 \\ 5 / 20 & 3 / 20 & 1 / 20 & 2 / 20 & 5 / 20 & 4 / 20 \\ 4 / 18 & 2 / 18 & 3 / 18 & 5 / 18 & 3 / 18 & 1 / 18 \\ 2 / 23 & 3 / 23 & 7 / 23 & 4 / 23 & 2 / 23 & 5 / 23 \end{matrix}]

实际雨型向量X与第k类模式雨型V_k的贴近度σ_k计算公式如下：

（5）

σ_{k} = 1 - \sqrt{\frac{1}{m} \sum_{i = 1}^{m} (v_{k i} - x_{i})^{2}}

若实际雨型与第k类模式雨型的贴近度最大，则认为该场降雨过程属于第k类雨型。

1.2.2 概率分布模型及检验方法

为计算不同重现期5 min至3 h的短历时降雨极值，首先对降雨极值进行概率分布模拟。由于降水的区域特征差异明显，目前尚无统一的极值概率分布模型。因此，模型的选择主要取决于其对极值样本分布的拟合效果及实际应用中所侧重的概率范围。本文采用的拟合模型计算方法参见《气候可行性论证规范极值概率统计分析》（全国气候与气候变化标准化技术委员会，2019）。采用柯尔莫哥洛夫-斯米诺夫（Kolmogorov-Smirnov）检验法（简称“K-S检验法”）（毛慧琴等，2004）和拟合相对偏差法评价上述分布模型对极值降水序列的模拟效果。

K-S检验通过计算假设理论分布F（x_i）与经验概率分布F_w（x_i）在每个样本点的概率差的最大值D_n（即K-S统计量），判断样本是否符合假设理论分布。D_n的计算公式如下：

（6）

D_{n} = m a x (|F (x_{i}) - F_{w} (x_{i})|)

在给定显著性水平α和样本量n的情况下，通过查表获得K-S检验的临界值λ_α，n。若D_n<λ_α，n，则接受原假设，认为样本符合假设理论分布，否则拒绝原假设。

本文选择显著性水平α=0.05，根据样本量查表得到λ_α，n=1.36，当D_n<λ_α，_n时，样本符合假设理论分布，且D_n越小，模型拟合效果越优。

拟合相对偏差R用于评估拟合值与实际值的偏差大小，其计算公式如下：

（7）

R = 100 \times \frac{1}{n} \sum_{i = 1}^{n} \frac{|y_{i} - {\hat{y}}_{i}|}{y_{i}}

式中：y_i为第i个样本的实际值， ${\hat{y}}_{i}$ 为模型拟合值。拟合相对偏差R越小，模型拟合效果越优。

2 暴雨雨型及极值重现期

2.1 西宁市暴雨日数的变化特征

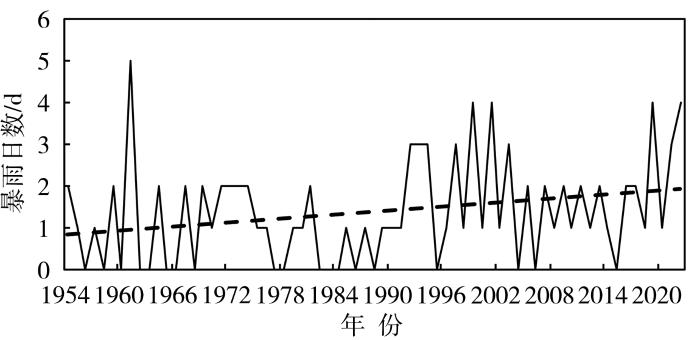
1954—2022年，西宁市日降水量大于等于25.0 mm的暴雨过程共计95场，平均每年约1.4场；日降水量超过50.0 mm的暴雨有7场，占暴雨总场次的7.4%；年际变化显著，1990年之前有42%的年份未出现暴雨，而1990年后有12%的年份未出现暴雨，整体呈缓慢增加趋势；年暴雨日数最多出现在1961年（5 d），有19 a未出现暴雨（图2）。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 1954—2022年西宁暴雨日数年际变化

Fig.2 Inter-annual variation of rainstorm days in Xining from 1954 to 2022

2.2 暴雨雨型统计

根据1.2.1暴雨判定标准，将1954—2001年和2011—2022年出现的75场暴雨，基于逐分钟降水资料开展雨型统计。将24 h的暴雨过程均分为6个阶段（20：00—23：00、00：00—03：00、04：00—07：00、08：00—11：00、12：00—15：00、16：00—19：00）（王彬雁等，2015），计算每阶段雨量占过程雨量的比例，根据贴近度分析确定每场暴雨的雨型，统计各雨型的出现次数及其占比，结果如表1所示。峰值位于前部的Ⅰ类雨型占比最大（44.0%），其次是峰值位于中部的Ⅲ类雨型，Ⅳ、Ⅵ类雨型占比最少，均为2.7%。单峰型雨型（Ⅰ、Ⅱ、Ⅲ类）占总暴雨场次的85.3%。

表1 西宁市75场暴雨雨型统计

Tab.1 The rainstorm pattern statistics of 75 events in Xining

雨型	出现次数/次	占比/%
Ⅰ	33	44.0
Ⅱ	6	8.0
Ⅲ	25	33.3
Ⅳ	2	2.7
Ⅴ	3	4.0
Ⅵ	2	2.7
Ⅶ	4	5.3

新窗口打开| 下载CSV

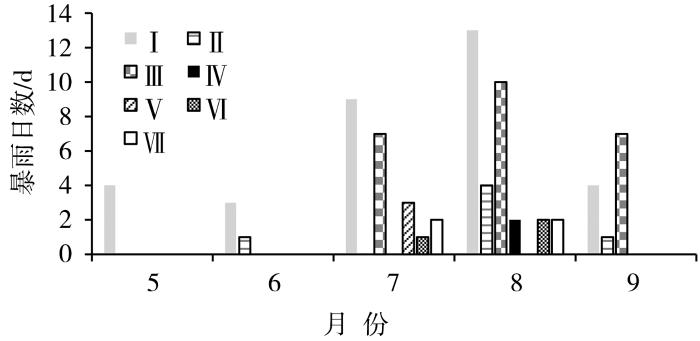
从7类雨型的月分布特征（图3）可见，西宁暴雨主要集中在7—9月，占比达89.0%，其中8月出现暴雨次数最多。5月仅出现Ⅰ类雨型；6月以Ⅰ、Ⅱ类单峰雨型为主；7月，单峰型雨型（Ⅰ、Ⅲ类）占比较高，其中Ⅰ类雨型最多，双峰型雨型（Ⅴ、Ⅵ、Ⅶ类）出现6次；8月单峰型雨型最多，主要为Ⅰ类，与7月不同，8月Ⅱ类雨型和均匀型Ⅳ类雨型均较多，且Ⅳ类雨型仅出现在8月；9月仅出现单峰型雨型，以Ⅲ类为主。西宁市暴雨雨型以单峰型为主，占比达85.3%，双峰型和均匀型暴雨较少，仅在7、8月出现。这一分布特征与何永晴等（2019）利用芝加哥雨型法得到的西宁市暴雨雨型特征一致，表明西宁市暴雨强度通常集中在降雨过程的前半段。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 西宁市5—9月不同雨型暴雨日数分布

Fig.3 Distribution of heavy rain days with different rainstorm patterns in Xining from May to September

2.3 暴雨雨型分析

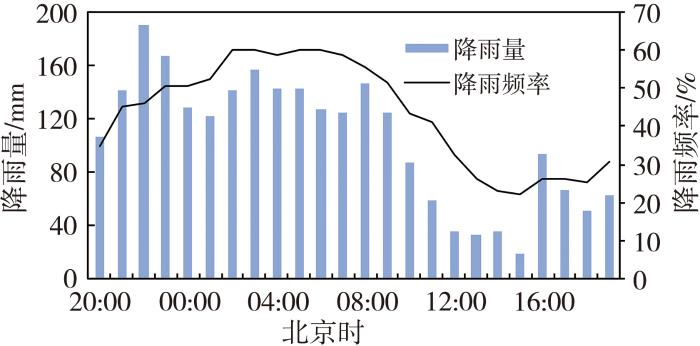
对筛选出的75次暴雨过程的累积雨量和降水频率进行日变化分析（图4）发现，西宁汛期暴雨雨量的高值区出现在20：00—次日09：00，占总雨量的78.4%；而暴雨出现次数的高频时段为23：00—次日09：00，占总暴雨次数的71.5%。上述两个时段并未完全重合，可总结为“前半夜下的大（雨量），后半夜下的多（频率）”。这一特征与刘义花等（2020）的研究结论一致，可能与西宁市位于山谷地区的地形特征有关（Guo et al.，2014；于竹娟等，2024），夜间地面辐射冷却，密度较大的冷空气沿山坡下沉至谷底或盆地，汇聚后被迫抬升，在谷底湿润空气条件下易形成云雨。此外，西宁汛期午后多强对流天气，因此16：00—19：00出现了降雨的次高值区，而11：00—15：00是暴雨发生的最少时段。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 西宁市暴雨过程降雨量和降雨发生频率的日变化

Fig. 4 Diurnal variation of rainfall amount and frequency in Xining during heavy rain processes

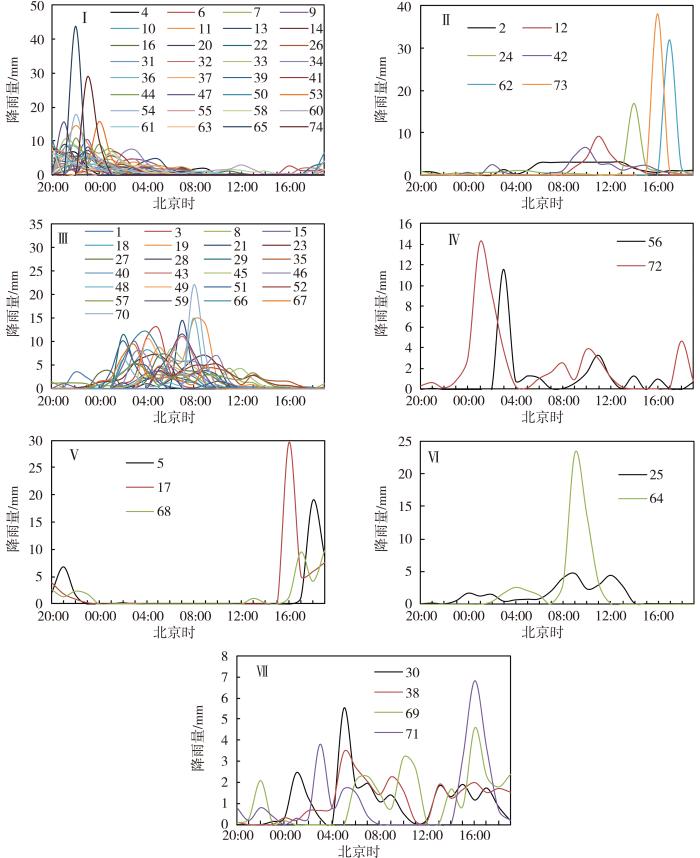
根据贴近度原则，将75次暴雨过程划分为7类雨型，并绘制各类型暴雨过程的降雨时程图（图5）。暴雨雨量在时间上的分布极不均匀，单一雨型难以全面描述一日内暴雨的变化特征。Ⅰ类雨型峰值主要出现在21：00—00：00，随后逐渐减少，小时降雨量最大可达43.7 mm；Ⅱ类雨型峰值出现在13：00—17：00，小时雨量最大可达38.1 mm；Ⅲ类雨型峰值分布跨度较大，集中于02：00—10：00，小时雨量最大为22.0 mm，是单峰型中峰值雨量最小的雨型；Ⅳ类雨型降雨过程中出现多个峰值，各峰值雨量均较小。Ⅴ、Ⅵ、Ⅶ类雨型均为双峰型，其峰值主要分布于13：00—17：00、00：00—10：00。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 西宁市7类雨型的降雨量逐小时变化

（图例中的数字为75场降雨过程的顺序编号）

Fig.5 Hourly variation of rainfall of the seven rain patterns in Xining

（The numbers in figures represents the sequence identifiers of 75 rainfall processes）

2.4 降雨极值的概率分布模拟与重现期计算

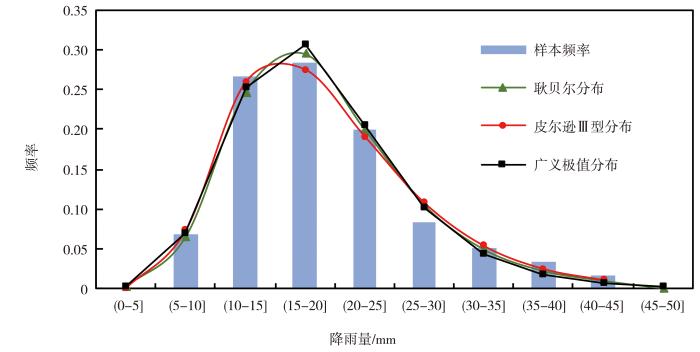
以西宁不同降雨历时的年最大降雨量作为极值样本，进行概率密度分布模拟。样本频率表示降雨量从0 mm开始，以5 mm为步长的每个前开后闭区间内的次数占总降雨次数的比例。以150 min为例，图6显示，3种分布模型与样本频率分布的趋势基本一致，均较好地反映了降水样本的频率特征。其中，耿贝尔分布和广义极值分布在样本频率最高的区间存在模拟值偏高的情况。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 西宁市150 min历时降水极值频率分布与耿贝尔分布、皮尔逊Ⅲ型分布、广义极值分布模拟的概率密度分布

Fig.6 Frequency density of 150-minute precipitation extreme and probability density fitted by Gumbel distribution，Pearson-Ⅲ distribution，Generalized Extreme Value distribution in Xining

为确定不同降雨历时最优的概率分布模型，对11个历时的3种概率分布模型进行检验，检验指标选取K-S统计量D_n、相关系数r和拟合相对偏差R，结果见表2。

表2 西宁不同历时降雨极值拟合效果检验

Tab.2 Fitting value verification of precipitation extreme for different duration in Xining

历时/min	D_n			r			R
历时/min	Gumbel	P-Ⅲ	GEV	Gumbel	P-Ⅲ	GEV	Gumbel	P-Ⅲ	GEV
5	0.068	0.067	0.077	0.987	0.988	0.997	6.863	5.222	6.503
10	0.066	0.067	0.066	0.994	0.990	0.995	4.749	5.102	5.855
15	0.050	0.046	0.072	0.998	0.998	0.994	4.639	3.293	5.899
20	0.078	0.058	0.091	0.972	0.985	0.983	7.223	3.588	7.923
30	0.090	0.051	0.129	0.957	0.992	0.981	9.962	3.984	10.568
45	0.098	0.073	0.144	0.945	0.993	0.948	10.830	4.091	11.283
60	0.112	0.076	0.149	0.942	0.985	0.914	11.508	5.175	11.110
90	0.076	0.070	0.121	0.961	0.969	0.973	7.639	4.027	8.646
120	0.057	0.060	0.082	0.986	0.981	0.993	4.263	3.268	5.720
150	0.044	0.052	0.051	0.994	0.995	0.994	2.443	2.574	3.180
180	0.079	0.078	0.075	0.916	0.914	0.915	3.896	3.197	3.355

注： Gumbel、P-Ⅲ、GEV分别表示耿贝尔分布、皮尔逊Ⅲ型分布、广义极值分布。

新窗口打开| 下载CSV

3种概率分布模型均通过K-S检验。在模拟15~120 min历时的降雨时，皮尔逊Ⅲ型分布的D_n小于耿贝尔分布和广义极值分布，表明皮尔逊Ⅲ型分布拟合效果更好；但在较短（5、10 min）和较长（120~180 min）历时降雨模拟中，皮尔逊Ⅲ型分布的D_n大于耿贝尔分布和广义极值分布。3种概率分布模型的相关系数均达到极显著水平（P<0.001），皮尔逊Ⅲ型分布的整体相关性最强。3种概率分布模型的拟合相对偏差R的特征与D_n类似，即皮尔逊Ⅲ型分布拟合15~120 min降雨历时的效果更好，其余则耿贝尔分布和广义极值分布拟合效果更好。3种概率分布模型45、60 min历时的拟合效果均相对较差。

基于皮尔逊Ⅲ型概率分布，计算西宁不同降雨历时的重现期降雨极值（表3），可看出，各重现期降雨极值随降雨历时增加而增大。2~100 a的6个重现期（上海市政工程设计研究总院（集团）有限公司，2021）内，5 min历时降雨极值为4.2~11.5 mm，60 min历时降雨极值为11.9~39.4 mm，180 min历时降雨极值为19.5~45.6 mm。Ⅰ类雨型中最大雨强达43.7 mm·h^-1，已超过100 a一遇的水平；Ⅱ类雨型中最大雨强达38.1 mm·h^-1，超过50 a一遇水平，Ⅴ类雨型中最大雨强接近20 a一遇水平，其他雨型最大雨强在2 a一遇到10 a一遇之间。在城市防灾减灾工作中，应更注重强度峰值出现在傍晚至午夜的Ⅰ类、Ⅱ类雨型暴雨的影响。

表3 基于皮尔逊Ⅲ型概率分布函数的西宁不同历时重现期降雨极值

Tab.3 Short-duration precipitation extreme values with different return periods in Xining based on Pearson-Ⅲ probability distribution function 单位：mm

重现期/a	降雨历时/min
重现期/a	5	10	15	20	30	45	60	90	120	150	180
2	4.2	6.3	7.6	8.4	9.6	10.6	11.9	14.0	15.9	17.9	19.5
5	6.2	9.4	11.6	13.1	15.1	17.0	18.6	21.0	23.0	25.1	27.0
10	7.6	11.4	14.2	16.3	18.9	21.6	23.5	25.8	27.7	29.7	31.8
20	8.8	13.3	16.7	19.2	22.6	26.1	28.4	30.5	32.3	33.9	36.2
50	10.3	15.6	19.8	23.0	27.4	32.0	34.7	36.6	38.0	39.2	41.6
100	11.5	17.3	22.1	25.8	30.9	36.5	39.4	41.1	42.2	43.1	45.6

新窗口打开| 下载CSV

3 结论与讨论

本文基于西宁市近69 a日降水资料和1954—2001、2011—2022年共60 a的逐分钟降水资料，利用模糊识别法识别雨型，对不同雨型进行统计分析，对比3种概率分布模型对不同历时降水的拟合优度，计算短历时降雨重现期，得到以下主要结论。

1）1954—2022年，西宁市暴雨共95场，其中日降水量超过50.0 mm的暴雨有7场，占暴雨总场次的7.4%。年暴雨日数最多为5 d（1961年），平均每年约1.4 d，总体呈缓慢增加趋势。

2）西宁市暴雨以单峰型为主，占总暴雨场次的85.3%，主要集中在7—9月。单峰型降雨中，峰值多位于降雨过程的前中期，峰值雨强最高达43.7 mm·h^-1。双峰型和均匀型暴雨较少，仅出现在7、8月。暴雨雨量高值区集中在20：00—次日09：00，而暴雨频率高值时段为23：00—次日09：00，表现为“前半夜下的大（雨量），后半夜下的多（频率）”的特征。

3）3种概率分布模型的模拟均能通过K-S检验，皮尔逊Ⅲ型分布的拟合效果更好。各重现期内，降雨极值随历时增加而增大。Ⅰ类和Ⅱ类雨型中的最大雨强分别超过60 min历时的100 a一遇和50 a一遇水平，致灾可能性更高。

西宁市暴雨多为单峰型，雨量集中、强度大，且多发生在夜间，具有较高致灾风险。应重点关注夜间强降雨引发的城市内涝及其次生灾害。在气候可行性论证和城市防涝工程设计中，应结合不同雨型的降雨时程和重现期降雨极值进行标准化的风险评估与方案设计，为重大工程项目建设和城市防灾减灾提供科学依据。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

岑国平, 沈晋, 范荣生, 1998.

城市设计暴雨雨型研究

[J]. 水科学进展, 9(1):41-46.

[本文引用: 3]

[2]

谌芸, 孙军, 徐珺, 等, 2012.

北京721特大暴雨极端性分析及思考(一)观测分析及思考

[J]. 气象, 38(10):1255-1 266.