0 引言
干旱一般具有范围广、时间长、影响行业多的特点,是世界上最严重的气象灾害。长时间的干旱对农业生产、粮食安全、水利发电及人民生活和动植物生态环境等形成危害。近年来全球每年因干旱造成的损失达60~80亿美元,超过其他气象灾害损失(宋艳玲,2022)。我国干旱发生也较为频繁,如2022年就发生大范围的干旱,南方大面积区域干旱达特旱等级(杨晓静等,2023;宋刚勇等,2023;雷声等,2023;孙伟等,2023)。干旱危害影响严重,其形成因素又较为复杂,与降水、气温、风速、辐射等气象要素密切相关(潘永地等,2022),精准监测干旱出现时间、结束时间,评估干旱的强度、范围都十分困难。为了准确监测和评估干旱,广大科技工作者建立了气象、水文、农业等干旱指数。其中,标准化降水指数(Standardized Precipitation Index,SPI)(McKee et al.,1993)被广泛使用,用于描述不同时间尺度上的气象干旱,通过历年同期降水量确定概率分布曲线,再由当年该时期内降水量的累积概率确定干旱指数。SPI以一定时间尺度中降水量所处概率等级来计算,反映当年该时间尺度中降水量与历年同期降水量比较的情况,多用于分析区域的干旱时空特征(商守卫等,2022;唐怡等,2023;黄瑶等,2023;任至涵等,2024;阿帕尔·肉孜等,2024),但仅采用降水量作为计算输入要素,不能体现日照、气温等对蒸散的影响。同时,SPI计算中确定时间尺度具有一定的主观性,不同时间尺度可能会出现不同结果(李家誉等,2022;朱占云等,2024)。此外,降水序列并不总是服从Gamma分布,考虑了分布函数参数随时间变化的非一致性标准化降水指数能更精确反映实际干旱情况(陈灏等,2023)。标准加权平均降水指数(Standard Weighted Average Precipitation Index,SWAP)在SPI基础上考虑了前期降水对干旱影响的衰减,也就是考虑径流、渗透、蒸散等失水项随着干旱发展而减弱的作用,其在计算累积降水时,加入了权重系数(Lu,2009),该系数由间隔时间和衰减参数计算。SWAP在计算累积降水时加入了与日期有关的权重,体现出干旱越重,土壤中含水量越小,径流、渗透、蒸散等失水项所受制约越大,较SPI更接近实际情况,但是计算中衰减参数的确定具有经验性,其时间尺度的选择也有一定的主观性,给实际应用增加了困难(杨家伟等,2019)。标准化降水蒸散指数(Standardized Precipitation-Evapotranspiration Index,SPEI)(Vicente-Serrano et al.,2010)在SPI基础上引入潜在蒸发,以降水量与潜在蒸发的差值累积替换SPI中的累积降水量,较SPI考虑了更多因素,更能反映实际情况,被广泛应用于干旱空间分布和趋势变化分析(周丹等,2014;廉泓林等,2022)。虽然SPEI较SPI更接近实际,但也没有考虑实际蒸散强度与干旱程度有关这一因素,另外在冬季且时间尺度小于3个月时,一些干旱地区的样本不服从Log-logistic分布(王林和陈文,2014),SPEI应用上有一定制约。帕默尔干旱指数(Palmer Drought Severity Index,PDSI)(Palmer,1965)依据土壤水分平衡原理建立,通过计算出某区域气候适宜条件下的月尺度蒸散量、土壤水分补充量、产流量和土壤失水量,得出气候适宜降水量,再计算各月实际降水量与适宜降水量的差值以反映水分盈亏情况,水分盈亏标准化后形成干旱指数。PDSI考虑的因子较全面,包括降水、蒸散、径流等,物理过程清晰,对于一些流域的干旱研究有其优势(王姝等,2019),但其输入要素的时间尺度为月尺度,对干旱反应较滞后(Alley,1984)。此外,由于需用要素较多,搜集完整的历史数据序列也容易遇到困难。常年降水百分比指数(Percentage of Normal Precipitation,PNP)以当年某段时间降水量与同期常年降水量的百分比来衡量,计算简单方便,但考虑因素单一,时间尺度不同会得出不同的结果。加权异常标准化降水指数(Weighted Abnormal Standardized Precipitation,WASP)(Lyon,2004)仅考虑降水偏少引发干旱,以月降水格点数据作为输入项,虽其计算简便,但与PNP一样,未体现蒸发这一干旱形成的重要因素。同时,WASP对于常年干旱或常年湿润地区的情况不能正确描述,有些区域降水格点历史数据不易获得也限制了其使用。为了适应不同的应用,多种类型的农业干旱指数(Palmer,1968;Hahm et al.,2022)、水文干旱指数(Arslan,2021;Tareke and Awoke,2022)、遥感干旱指数(郑超磊等,2021;Nourani,2022)相继被建立起来。在这些指数基础上,也出现了一些描述干旱的综合性指数(Zhu et al.,2016;Cammalleri et al.,2021;吴志勇等,2021)及用来评估干旱的综合性系统。
本文从反映干旱程度的土壤含水量干旱等级划分标准出发,通过理论推导维持土壤干旱等级的累积降水和累积水面蒸发关系,建立计算简便的干旱等级判定和干旱指数模型。该模型可以逐日滚动计算,选取的时间尺度具有客观性和唯一性,不依赖历史气候概率,可以更科学快速地监测干旱的发展。
1 资料与方法
1.1 资料
目前自动站土壤水分观测数据误差较大,浙江平阳气象站有2013年较完整的土壤水分人工观测资料,所以用该站土壤水分数据做检验。由于2022年温州全市都受干旱影响,温州站作为国家气象观测站更有代表性,典型年份旱情发展检验时用温州站资料;温州站降水和蒸发观测资料序列较长,在历史干旱反演检验中采用温州站资料。具体所用资料:2013年1月18日—9月28日平阳气象站每旬1次的10~20 cm土壤含水率、土壤相对湿度测量数据,用于验证构建的干旱指数与土壤湿度的相关性;2012—2013年平阳气象站逐日降水量、逐日小型蒸发皿蒸发量,用于计算2013年平阳站干旱指数;温州气象站1984—2022年逐日降水量和逐日大型蒸发皿蒸发量,用于计算1985—2022年温州站干旱指数;2022年温州旱情调查情况及1985—2022年温州历年气候影响评价和年鉴中干旱灾情,用于验证构建的干旱指数对干旱的捕捉及反演效果。
1.2 方法
从影响作物生长、直观反映干旱程度的土壤相对湿度出发,通过土壤水分平衡方程,推导维持干旱等级的降水量-水面蒸发量关系,建立各干旱等级维持线表达式;再通过前向逐日滚动计算累积降水量、累积水面蒸发量,由两者确定出坐标位置,计算该坐标点与干旱等级维持线的逐日距离变化。累积降水量、蒸发量计算起始日由具有最大距离的坐标点对应确定,再根据该最大距离计算干旱指数,建立土壤干旱等级距离指数模型。由该干旱指数模型计算平阳站2013年的逐日干旱指数、温州站2022年逐日各干旱等级维持线距离及1985—2022年的逐日干旱指数,将计算结果与土壤湿度观测记录、实际的旱情记录进行对比,证明该干旱指数与土壤湿度存在极强的负相关,对旱情演变的描述与实际情况吻合。
1.2.1 干旱等级
表1 基于土壤相对湿度的干旱等级划分
Tab.1
| 10~20 cm深度土壤相对湿度(R) | 干旱等级 |
|---|---|
| R>60% | 无旱 |
| 50%<R≤60% | 轻旱 |
| 40%<R≤50% | 中旱 |
| 30%<R≤40% | 重旱 |
| R≤30% | 特旱 |
表2 基于土壤干土层厚度的干旱等级划分
Tab.2
| 干土层厚度(H)/cm | 干旱等级 |
|---|---|
| H<5 | 无旱 |
| 5≤H<10 | 轻旱 |
| 10≤H<15 | 中旱 |
| 15≤H<20 | 重旱 |
| H≥20 | 特旱 |
1.2.2 干旱等级维持线
干旱达到一定程度后,要维持土壤的干旱等级就必须使土壤中输入输出的水分保持平衡,即
式中:
正常情况下不同的植被覆盖土壤蒸散量差异较大,但在干旱条件下的植被蒸腾远小于水面蒸发,所以本文研究区域忽略植被的蒸腾。故处于干旱状态下,公式(1)中的
张瑜芳等(1991)研究表明,随着干旱发展,土壤表面形成干土层后,在表层土壤低含水率条件下,土壤蒸发与水面蒸发成线性关系:
式中:
由此可见,在干旱达到土壤表面有干土层后,若维持干土层厚度不变,则土壤蒸发与水面蒸发成正比,其比率是干土层厚度的线性函数。根据公式(2),若增加的降水量要与土壤蒸发量相等,则干旱程度维持不变,所以由公式(2)和(3)得出:
式中:
式中:
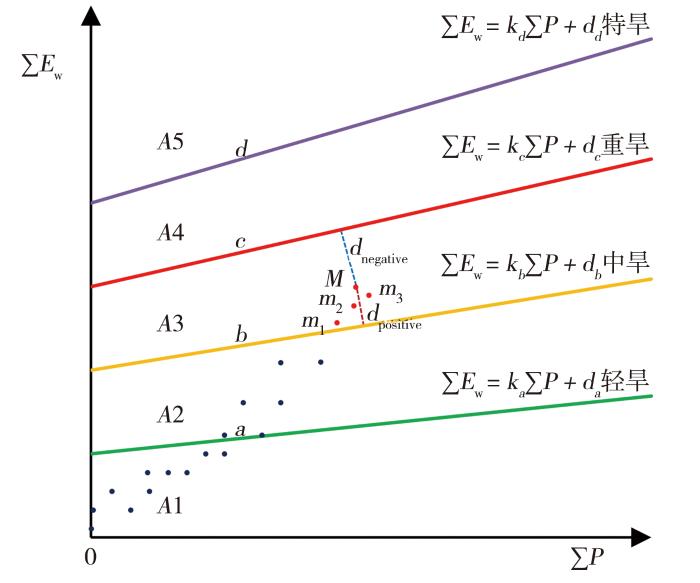
图1
图1
土壤干旱等级距离指数概念模型示意图
(点、线等说明见文中)
Fig.1
Schematic diagram of the conceptual model of soil drought grade distance index
(Points,lines,etc.,see the article)
由适宜含水量下限发展到各干旱等级,土壤中蒸发掉的水分计算公式如下:
式中:
图1中直线a、b、c、d分别是轻旱、中旱、重旱、特旱4个干旱等级的临界线;A1、A2、A3、A4、A5分别表示无旱、轻旱、中旱、重旱、特旱区域;ka、kb、kc、kd分别是对应临界线的斜率,经计算分别为2.027 4、2.477 4、2.927 4、3.377 4;da、db、dc、dd分别为对应临界线的截距,经计算分别为79.3、101.8、123.5、148.5 mm;
对于不同地区、不同作物,各干旱等级临界线的截距可以根据实际需要改变,也可以根据干旱指数计算结果与野外考察确定干旱等级来反推截距,而使干旱模型更适用于某地区某作物。
1.2.3 累积降水量、累积水面蒸发量
从哪一天开始计算累积降水量、累积水面蒸发量是干旱程度判别的关键,确定的起始日期要有客观性、唯一性,能反映目前干旱对作物造成的影响。采用逐日滚动最大距离法确定累积降水量、累积水面蒸发量。从评估当天开始,往前累加一天得到一个累积降水量和一个累积水面蒸发量,确定一个坐标点;这个点一般在坐标原点附近,该点到干旱等级维持线a有一个距离,再往前累加一天得到第2个点,这个点到直线a也有一个距离;比较这两个距离,选取大的距离作为准最大距离参与后续比较。以此类推,通过不断往前逐日累加得到新坐标点,并计算新点到直线a的距离,与前面得出的准最大距离比较,确定出新的准最大距离,直到准最大距离不再被更新(根据实际经验,准最大距离在连续累加90 d后就可以停止计算),这个准最大距离点就是直线a最大距离点,假设是图1中的m1点。同样地,可以得出b、c、d线对应的最大距离点,假设分别为m2、m3、M点。一般来讲,m1、m2、m3、M点可能是重合的,那么这个重合点就是评估日最终的最大距离点;若有不重合,在这4个点中,假设M点位于最高等级干旱区域,并且M点到下面最近的直线b距离最大,则将M点确定为评估日最终的最大距离点。M点到下方最近的直线b的距离dpositive就是评估当期干旱过程的最大距离,M点所对应的累积降水量、累积水面蒸发量决定了点坐标,也就决定了干旱指数计算结果,且该累积量对应的起始日就是当期干旱过程的起始日。前面是为了叙述方便,分开说明如何得出4条直线的最大距离点。在实际计算时,可以在每次滚动累加时同时计算出4条线的准最大距离点,从而提高效率。
1.2.4 土壤干旱等级距离指数
累积降水量、累积水面蒸发量在坐标中的位置M点(图1)所处区域对应该区域干旱等级。M点位于某临界线之上,该坐标点到临界线的距离为正,反之为负。将轻旱、中旱、重旱、特旱定义为1、2、3、4级,临界线上的干旱指数分别赋值1、2、3、4。
1)M点在A2、A3、A4区域的土壤干旱等级距离指数(简称“干旱指数”)I定义如下:
式中:L为M点所处区域的干旱等级,
2)为了干旱指数的连续性,当M点在A1区域时,下方无临界线,构建的指数如下:
式中:
3 )M点在A5区域时,上方无临界线,构建指数如下:
式中:
这样,构建的土壤干旱等级距离指数I数值在(0,5)区间,当I在(0,1)区间时无旱,[1,2)区间时轻旱,[2,3)区间时中旱,[3,4)区间时重旱,[4,5)区间时特旱。
2 结果和分析
2.1 干旱指数模型计算结果与土壤水分测量记录的相关性
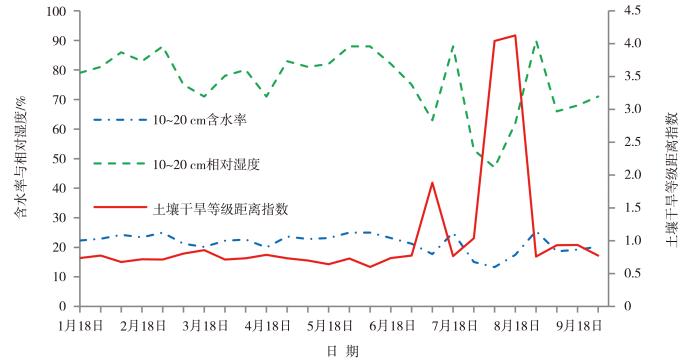
计算2013年平阳气象站的逐日土壤干旱指数,并与该站2013年每旬1次的定期土壤水分测量数据进行比较,结果见图2。
图2
图2
2013年1—9月平阳站土壤干旱等级距离指数与土壤含水率及土壤相对湿度演变
Fig.2
Evolution of soil drought grade distance index,soil water content,and soil relative moisture at Pingyang Station from January to September in 2013
由于自动观测的土壤水分资料准确性较低,人工长时期连续观测的土壤水分资料很少,因此以平阳县气象局在安装自动观测仪器前开展的连续9个月每旬1次的土壤观测资料进行检验。从图2看出,用构建的干旱模型计算出的干旱指数与实际测量的土壤含水率及土壤相对湿度变化趋势基本保持相反状态。在干旱过程中,土壤干燥,含水率低,对应的干旱指数就高。经过反正切归一化处理后,干旱指数与10~20 cm土壤相对湿度、含水率的相关系数分别达-0.835、-0.833。通过t检验,其零假设为真的条件下观察到当前样本数据概率Sig值分别为8.27×10-7、7.50×10-7,均通过0.001的显著性检验。可见,由本文确定的坐标点(累积降水量,累积蒸发量)到土壤干旱等级临界线的距离能反映土壤缺水程度,由该距离计算出的土壤干旱等级距离指数可以很好地描述土壤水分的变化趋势,可以客观监测、评估干旱的发展。该指数能够反映土壤干旱的原因在于模型构建时考虑了降水量和蒸发量两个因子的综合作用,并且其确定出的降水和蒸发累积量起始日实质上确定了无有效降水持续期的起始日。贺双燕等(2024)在分析2022年江西省干旱时空演变时发现,20 cm土壤湿度与月尺度的SPI相关系数达0.68,与季尺度的SPI相关系数为0.44,与半年尺度的SPI相关系数为0.56。Oyounalsoud等(2023)分析SPI、PDSI、SPEI、PNP等与深层土壤湿度的相关性,发现相关系数范围为0.2~0.6。传统干旱指数在选取的时间尺度或应用区域不同时,与土壤湿度的相关性存在较大差异,导致对不同区域、不同季节干旱的监测准确率不同(王莺等,2022),其中一个重要原因是降水亏缺累积时间尺度在不同区域具有差异性(张强等,2024)。土壤干旱等级距离指数选取时间尺度具有客观性,避免了因选取时间尺度不同而造成的相关性变化,并且与10~20 cm土壤湿度的相关性较其他气象干旱指数强,可以更好地用于干旱监测。
2.2 临界线距离对干旱过程变化的捕捉
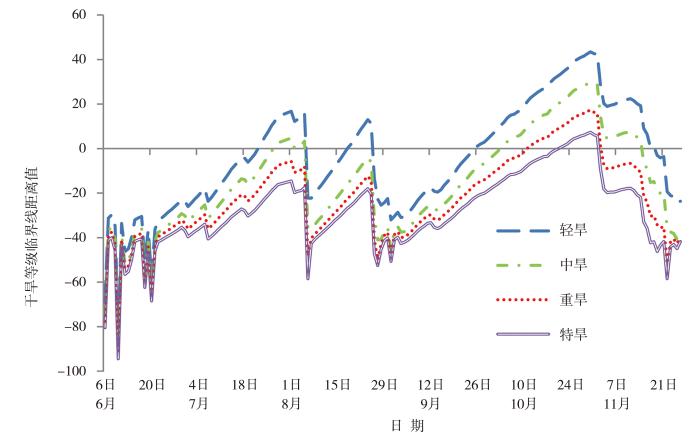
以各干旱临界线为基准,按1.2.3节确定的累积量起始日计算温州站2022年6月6日—12月31日期间逐日的累积降水量、累积蒸发量,确定坐标点,再计算该点到各临界线的距离(图3)。每一日由4条临界线计算出4个距离,若临界线距离能够捕捉干旱变化,则由这些距离计算出的干旱指数必然能反映干旱变化。临界线距离由负转正时表示达到该干旱等级,距离值越大表示干旱越严重;临界线距离由正转负时表示该干旱等级解除。
图3
图3
2022年6月6日—12月31日温州站土壤干旱临界线距离逐日变化
Fig.3
Daily variation of critical line distance for soil drought at Wenzhou Station from June 6 to December 31,2022
图3可以清晰地描述温州站2022年的干旱演变。2022年5月21日—6月21日,温州站出现持续阴雨天气,其间多暴雨过程,总降水量达380.7 mm,属于典型的梅涝;6月22日后多晴热天气,降水减少,6月30日及7月1、7、18、19日分别出现小雨过程。由干旱指数模型确定累积蒸发量、累积降水量的起始计算日是6月22日,6月22日—7月22日总降水量为19.3 mm,总蒸发量为121.9 mm;6月22日到7月21日,坐标点到各干旱临界线的距离均为负值,表明未达到轻旱,但逐渐接近0轴,即逐渐接近轻旱;7月22日,到轻旱的距离转为正值,表明开始出现轻旱,但到其他线的距离仍为负值;随着旱情发展,7月27日坐标点到中旱的距离也转为正值,达到中旱,但8月2日出现6.3 mm降水,干旱略有缓解,到中旱的距离又转为负值,旱情回到轻旱,8月3—5日又达到中旱,8月6日出现43.9 mm降水,旱情解除。临界线距离变化很好地刻画出这次干旱从6月22日逐渐发展,一直到8月3日达到中旱,又在8月6日解除的整个过程。8月8—24日又持续晴朗,8月18日到轻旱临界线距离转正值,达到轻旱。在8—10月,由于出现一些过程性降水,干旱发展过程中多次得到缓解,图3中都有清晰地展现。10月11日重旱临界线距离转为正值,表明旱情发展到重旱;10月21日,到特旱临界线距离转为正值,达到特旱;直到10月31日、11月1日出现小雨才逐渐缓解,11月2日出现中雨,旱情缓解为重旱,11月3日继续出现中雨,干旱等级为中旱;此后多天小到中雨,11月15日缓解为轻旱,11月19日轻旱临界线距离也转为负,表明旱情彻底解除。以上的干旱程度表达与实际的作物表现基本一致。根据温州市农业农村局的调查结果(温州市农业局,2022)显示:截至8月23日,全市共有9 700 hm2农作物不同程度受到旱情影响,包括水稻4 460 hm2、其他粮食作物1 307 hm2、蔬菜993 hm2、茶叶993 hm2、水果1 807 hm2;全市农作物成灾面积达2 200 hm2,绝收面积达553 hm2。2022年11月气候影响评价旱情总结(温州市气象局,2022)显示:2022年因干旱造成各地农用灌溉用水缺水严重,乐清、永嘉进行饮用水的限制性供水。其中鹿城区因无水源灌溉造成长期干旱的东魁杨梅果园受灾面积7 hm2、受灾茶园面积7 hm2;瓯海区因无水源灌溉造成无法播种的油菜面积7 hm2,无水源灌溉造成长期干旱的受灾蔬菜面积67 hm2、受灾果园面积7 hm2;乐清因无水源灌溉造成已播受灾的油菜面积8 hm2、无法播种的小麦面积9 hm2,无水源灌溉造成长期干旱的受灾蔬菜200 hm2、受灾果园(如杨梅、枇杷等)1 333 hm2、受灾茶园面积200 hm2;瑞安因无水源灌溉造成长期干旱的受灾蔬菜面积193 hm2、受灾果园面积130 hm2、受灾茶园面积193 hm2;文成因无水源灌溉造成长期干旱的受灾果园杨梅200 hm2、柑桔133 hm2、猕猴桃67 hm2、茶园67 hm2;苍南因无水源灌溉造成长期干旱的受灾果园(杨梅、荔枝、猕猴桃、柑橘等)面积210 hm2、受灾茶园面积400 hm2。本文构建的干旱指数对上述干旱实例的捕捉时间尺度精确到了日,而SPI、SPEI等的时间尺度一般在月以上更为敏感(Zhang et al.,2020),因此该干旱指数可以用于骤旱的识别、监测。
2.3 历年逐日土壤干旱等级距离指数与旱情记录
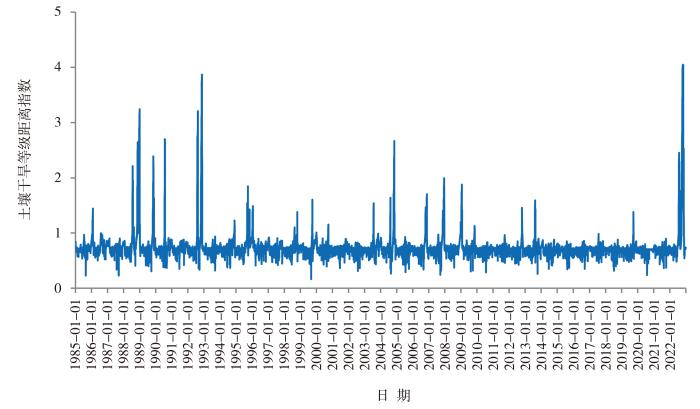
图4
图4
1985—2022年温州站土壤干旱等级距离指数逐日演变
Fig.4
Daily variation of soil drought grade distance index from 1985 to 2022 at Wenzhou Station
从图4可见,土壤干旱等级距离指数对历史干旱过程的反演结果与实际历史旱情记录基本一致。温州市气候影响综合评价(温州市气象局,1985—2022)显示:温州2022年出现特旱,1988、1992年出现重旱,1989、1990、2004年出现中旱。其中,2022年旱情在前面已有描述。1988年发生秋冬连旱,一些地方生活用水困难,火灾频发,一些水库干涸,柑桔等作物因干旱减产,冬种受到影响;1992年出现夏秋干旱,夏季干旱使早稻断水过早,高温逼熟,造成严重减产,瓜果、蔬菜等产量也受影响,部分晚稻田无水插秧,秋季又出现干旱,晚稻普遍断水过早;1989年出现秋冬连旱,火灾频发,山塘水库蓄水量剧减;1990年7月旱情发展迅速,稻田开裂,高温逼熟严重,蔬菜、蕃薯等作物因高温干旱而枯萎,晚稻无水移栽,干旱面积达44 000 hm2,成灾27 333 hm2,直接损失5 215万元人民币;2004年冬旱、夏旱、秋旱断续出现,山塘水库蓄水不足,各地农业灌溉用水紧张,森林防火极为严峻。
3 结论与讨论
本文通过干旱状态下的土壤水分平衡分析,简化了保持干旱等级不变条件下的土壤水分平衡方程,利用土壤水分平衡方程结合土壤干旱等级划分标准推导出干旱等级维持线的表达式,用逐日滚动最大距离法确定累积降水量、累积蒸发量,最终构建了土壤干旱等级距离指数。
1)指数模型中各干旱等级维持线的截距表示无降水条件下从适宜土壤含水量发展到相应干旱等级所对应的累积水面蒸发量,各干旱等级维持线的斜率表示在维持相应干旱等级条件下水面蒸发增加量与降水增加量的比率。
2)土壤干旱等级距离指数与土壤湿度相关性较好。该干旱指数的构成要素,即通过逐日滚动最大距离法确定的坐标点到各干旱等级维持线距离的变化能够精细描述旱情发展,对历年干旱的反演与实际旱情记录具有较好的一致性。
3)土壤干旱等级距离指数计算过程中的累积降水量和累积水面蒸发量既有明确的物理意义,也有确定累积起始日的客观方法;同时,不需要土壤湿度观测数据却能得到与土壤湿度分布较为一致的旱情评估结果。
4)土壤干旱等级距离指数逐日滚动计算,可以反映逐日干旱变化。
本文构建的土壤干旱等级距离指数所需要素少,只依据蒸发量和降水量数据计算,不依赖历史数据,为缺乏长历史观测数据序列区域的气象干旱监测、评估提供了可能。构建模型中假设的土壤参数与实际土壤可能存在差异,不同区域修改干旱等级对应的干土层厚度、土壤含水量,可以建立局地适应性更强的干旱等级维持线。
参考文献
基于SPI的1961-2020年昌吉地区作物生长季气象干旱时空特征研究
[J].
基于标准化降水蒸散指数(SPEI)的毛乌素沙地1981—2020年干旱特征研究
[J].大气干旱是影响半干旱沙区植被建设、生态恢复及社会经济可持续发展的重要因素。基于1981—2020年毛乌素沙地10个气象站点的逐月气象资料,计算了月、季和年尺度的标准化降水蒸散指数(SPEI),分析了该沙区近40年降水和气温的变化趋势、干旱事件及其频率的时空特征。结果表明:(1)毛乌素沙地近40年降水量和气温均呈现显著的上升趋势(P<0.05);秋季和冬季降水量呈现显著的上升趋势(P<0.05),四季气温均呈现显著的上升趋势(P<0.05)。(2)毛乌素沙地总体上呈现出不显著的湿润化趋势(P>0.05),但秋季呈显著的湿润化趋势(P<0.05);中、西部地区呈现出湿润化趋势,而东部地区则呈现干旱化趋势。(3)近40年毛乌素沙地的月尺度下干旱总频率达32.71%,各等级发生频率为轻旱>中旱>重旱>特旱,季节发生频次为冬季>夏季、秋季>春季;轻旱主要发生在毛乌素沙地的北部、中部、东南和西南部,中旱在东部、北部和西部边缘,重旱在东部、中部以及南部地区,特旱在西北部、南部和东南部区域。
基于最优概率分布函数的成都市近63 a干旱特征分析
[J].研究成都市不同尺度干旱时空分布特征对该地区农业、经济发展及干旱防灾减灾等具有重要意义。利用成都市14个国家气象站1960—2022年逐月降水数据,选择标准降水指数(Standardized Precipitation Index,SPI),首先通过对SciPy库概率分布函数的优选,确定成都市14个国家气象站年及季降水序列的最优概率分布函数;其次,基于最优概率分布函数分别计算得到年尺度和季节尺度的SPI(分别简称“SPI<sub>12</sub>、SPI<sub>3</sub>”);最后,基于SPI<sub>12</sub>和SPI<sub>3</sub>分析成都市年、季尺度干旱的时空分布特征。结果表明:不同尺度降水序列最优分布函数均通过K-S检验(显著性水平α=0.05),最优概率分布函数均能很好地表征成都市不同尺度降水序列的分布特征。成都市年及四季干旱站次比、干旱强度均呈弱增强趋势。年及四季干旱频率为25.40%~36.51%,不同尺度干旱频率的空间分布存在较大差异,相比秋旱和冬旱,春旱和夏旱发生频率略高。成都市14个区(市、县)不同等级年旱、春旱、夏旱、秋旱和冬旱的空间分布具有较大差异,但均以轻旱和中旱发生频率较高。
标准化降水蒸散指数在中国干旱监测的适用性分析
[J].针对国际上最新提出的干旱指数——标准化降水蒸散指数(SPEI),从拟合优度检验、对历史干旱事件的刻画、以及SPEI与SPI、PDSI指数的关系角度出发,全面分析了SPEI指数在中国区域的适用性。结果表明,只有在冬季且时间尺度小于3个月时,新疆南部、西藏西北部和华北至河套地区的样本不服从Log—logistic分布;而在冬季且时间尺度大于3个月以及夏季的任何时间尺度,中国范围的样本都符合Log—logistic分布,所得SPEI指数可靠。SPEI指数能够准确刻画几次特大干旱事件的地域中心、影响范围和强度。与SPI指数相比,SPEI指数引入了影响干旱的潜在蒸发项,能够更精确地刻画干旱。而与PDSI指数相比,SPEI指数具有多时间尺度特征,计算更简便。
基于历史帕默尔干旱指数(PDSI)数据集重建的长江源区过去706 a径流量
[J].利用亚洲季风区帕默尔干旱指数(PDSI)重建格点数据集(Monsoon Asia Drought Atlas,MADA)中长江源及附近地区的5个格点序列,通过PDSI与长江源区径流量的相关分析,发现5个格点的第一主成分(PC1)与长江源区夏季(6—8月)平均径流量的相关性最大(r=0.609,N=50,α<0.001)。由此,重建了1300—2005年长江源区夏季径流量变化,并运用独立验证法对重建结果的可靠性进行了检验,运用小波分析方法对重建径流序列进行周期分析。结果表明:近706 a,长江源区经历了显著的丰水期13个、枯水期15个,其中持续时间最长的丰水期为1513—1573年,持续时间最长的枯水期为1389—1414年;重建序列主要存在2~6、10~13、20~26、30~50、50~70 a的显著周期振荡。重建序列与海表温度的相关性表明,长江源区径流变化可能与厄尔尼诺-南方涛动(ENSO)、大西洋年际振荡(AMO)、北大西洋涛动(NAO)、太平洋年代际振荡(PDO)等有关。
21世纪以来干旱研究的若干新进展与展望
[J].干旱是中国影响范围最广、造成经济损失最严重的自然灾害之一,直接威胁国家粮食安全和社会经济发展,对干旱问题的认识和研究有助于提升国家防旱减灾能力。自新中国成立以来,中国对于干旱气象的研究取得了丰硕的成果。本文以21世纪以来中国气象局干旱气候变化与减灾重点开放实验室为平台开展的与干旱气象相关的科研项目群取得的研究成果为基础,通过成果检索,对干旱监测技术、干旱时空分布规律、干旱致灾特征、干旱灾害风险及其对气候变暖的响应以及干旱灾害风险管理与防御技术等方面的新进展进行总结和归纳。同时,基于干旱气象研究的前沿发展趋势,提出中国未来干旱气象研究应在加强气候变化背景下干旱高发区综合性干旱观测试验基础上,从不同维度和尺度定量研究干旱形成机理,构建多源数据融合和多方法结合的综合干旱监测新方法,揭示干旱致灾机理,科学评估干旱灾害风险,提出具有可执行性的风险管理策略等重点科学问题上取得突破。这对于推动中国干旱气象研究具有积极意义。
新安江流域气象干旱和水文干旱特征及两者之间的关系研究
[J].新安江流域是传统丰水区,对该区域进行干旱演变规律以及气象-水文干旱传播特征及其响应关系的研究,对于流域水资源的调度和管理具有重要科学意义。基于新安江流域近63 a的降水和径流数据,利用标准化降水指数(Standardized Precipitation Index,SPI)和标准化径流指数(Standardized Runoff Index,SRI),研究不同时间尺度的新安江气象干旱和水文干旱的演变规律,并分析流域水文干旱对气象干旱的时滞效应。结果表明:(1)1960—2022年新安江流域的气象干旱和水文干旱主要发生在20世纪60年代、70年代末到80年代中期以及21世纪初,2010年至今新安江整体处于水资源丰盈状态,其余时段则干旱与湿润交替发生。(2)近63 a的数据显示,新安江流域总体呈现变湿趋势,干旱事件有所减少。其中冬季和夏季变湿最为明显,且水文角度变湿趋势比气象角度更为明显。(3)新安江流域的水文干旱与气象干旱显著相关,通常在气象干旱发生后1~3个月出现。水文干旱对气象干旱在汛期的相关性和响应速度均高于非汛期。因此,应更加关注汛期的流域干旱并采取针对性措施。
The Palmer drought severity index: Limitations and assumptions
[J].
Hydrological drought analysis for Bolu city with streamflow drought index
[J].
A revision of the combined drought indicator (CDI) used in the European drought observatory (EDO)
[J].
Bedrock vadose zone storage dynamics under extreme drought: Consequences for plant water availability, recharge, and runoff
[J].
Comparing surface water supply index and streamflow drought index for hydrological drought analysis in Ethiopia
[J].
Determining the start, duration, and strength of flood and drought with daily precipitation: Rationale
[J].
The strength of El Niño and the spatial extent of tropical drought
[J].
A new meteorological drought index based on fuzzy logic: Development and comparative assessment with conventional drought indices
[J].
Application of the artificial intelligence approach and remotely sensed imagery for soil moisture evaluation
[J].
Keeping track of crop moisture conditions, nationwide: The new cropmoisture index
[J].
Meteorological Drought
[R].
Evaluation of time scale of meteorological, hydrological and agricultural drought indices
[J].
Causes and changes of drought in China: Research progress and prospects
[J].
A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index
[J].
Combined use of meteorological drought indices at multi-time scales for improving hydrological drought detection
[J].