金沙江下游地形复杂，峡谷沟壑遍布，且地形落差明显，该区域坐落有4个梯级水电站，构成中国的清洁能源走廊。金沙江流经云南巧家县与四川宁南县交界处，形成一条南北向的深切峡谷，水流从上游的葫芦口大桥经过约40 km的蓄水坝区，最终穿过水电站大坝到达下游的荒田，峡谷地形落差达近200 m。干季（11月至次年4月）降水稀少（胥良，2004；曹辉等，2018），但大风天气极为频繁且复杂，坝区7级以上大风天气年均200 d以上（陈文龙，2018），风速多次突破历史极值，对水电建设和电力输送构成严重威胁。因此，大风预警研究对于降低灾害风险和提高复杂地形预报水平具有重要意义。

研究表明，大风天气受雷暴、台风、锋面、气旋、低槽和急流等多尺度天气系统及地形综合影响，风速脉动强，预报难度大（周淑玲等，2014；李旭等，2015；付桂琴等，2015；朱男男等，2016；谭志强等，2017；王黉等，2019；吴琼和徐卫民，2019；刘兰等，2021）。通过分析这些天气系统活动和大气环境条件，特别是高空环流形势的变化、冷空气路径、下垫面的热力和动力作用，以及变压场和冷池的影响，并采用数值模拟和中小尺度气象学方法探究大风天气的形成机制（王艳兰等，2021）。地面风是气温、气压和湿度等气象要素变化的直接反映，对这些气象要素的定点精细化分析能够揭示大气流场的变化，为大风发生提供前期信号，对大风预报具有重要意义（潘留杰等，2023）。陈海涛等（2017）在对辽宁营口地区的大风预报研究中指出，大风通常发生在正变压中心附近的变压梯度最大处，当3 h正变压中心位于辽西，而负变压中心位于辽宁东北部至黄海一带时，可预报7级以上偏北大风。高梦竹等（2019）研究显示，地面大风易在地面低压区和冷高压前部形成。周淑玲等（2014）在山东近海大风的预报中，选择气压梯度、850 hPa以下的急流和850 hPa暖平流作为强偏南大风的重要预报因子。张晓芳和李宇华（2010）基于黑龙江伊春地区数据，建立大风预报模型时将单站气温日较差超过19 ℃和气压日较差为正设定为大风发生的关键指标。以上研究均表明，气压变化是大风预警的关键气象要素。在金沙江下游水电站的气象保障服务中，专家的观察和经验也证实了气压变化对风速预报的重要性。

金沙江下游峡谷区天气复杂多变，风速预报难度大，现有的数值模式和高空环流形势分析得到的风速预报结果无法满足电力作业的精细化需求。电力部门在峡谷区上下游布设的观测站积累了丰富的气象观测数据，为预报研究提供了参考信息。本文探索坝区干季大风天气地面观测站的气压变化特征及其与上下游风速变化的关系，旨在建立适用于特殊地形区的风速预报方法，为预防和预警影响水电建设和电力输送的强风灾害提供技术支撑。

金沙江自上游的葫芦口大桥起，经过南北向的“U”型地形流出峡谷（图1）。自2017年白鹤滩水电站全面开工以来，沿峡谷两侧陆续布设了多个加密观测站，主要用于风速监测和预警。其中，新田站观测数据连续且完整，2021年后又增设了荒田、坝顶、骑骡沟和葫芦口大桥站，观测网络得到加强。新田站位于水电站大坝附近，葫芦口大桥站位于峡谷上游，荒田站位于下游，测站的海拔高度从上游至下游依次降低。

鉴于雨季降水可能影响风速变化的因子较复杂，为降低其他因素的干扰，在构建大风事件数据集时选取新田站2020年和葫芦口大桥站2022年干季中1—3月和11—12月的无降水日数据，观测数据包括逐小时极大风速和气压以及2 min和10 min平均风速。

依据气象行业标准，将小时极大风速超过13.9 m·s^-1的7级风力等级或2 min平均风速超过10 m·s^-1定义为大风事件（尹晔等，2023）。大风事件中风速开始明显增加作为事件的起始时间，风速持续下降至7级风力以下作为事件结束时间；将风速开始增加前的气压峰值确定为气压最大值，气压降低的第一次谷值确定为气压最小值。新田站距离大坝近，有长期稳定的观测数据，能更准确地反映坝区风速，研究以该站为主，以上游的葫芦口大桥站和下游的荒田站为参照站。根据以上标准，从原始观测数据中筛选构建峡谷区大风事件数据集。

使用Granger（1969）在经济学领域提出的格兰杰因果检验方法确定峡谷区上下游大风天气发生时间的先后关系。此方法通过分析变量间的相互关系及其自身变化，有效地避免了变量间的伪相关性（刘劲龙等，2013）。分析步骤如下：

1）时间序列平稳性检验

使用增广迪基—富勒检验（Augmented Dickey Fuller Test）方法检验时间序列的平稳性。参考姚望玲等（2010）的方法，通过统计值t判断，若序列的差分值在给定显著性水平的临界值以下，则判定序列稳定。

2）格兰杰因果分析

对上游和下游大风发生的时间序列进行因果关系分析。基于曹鸿兴等（2008）的研究，通过以下公式建立滞后关系y_t：

式中：k为最大滞后阶数；i为自变量；et为误差项；αi、βi为yi和xi的回归系数；t为时间序列长度。

3）显著性检验

使用以下公式检验测站风速变化时间关系的显著性：

式中：SSEr为yt自回归时的残差平方和；SSEm为yt对xt所有滞后项的回归残差平方和；N为序列长度。若F对应的检验P值小于预设的显著性水平α，则判定下游站的大风事件滞后于上游站，本文取α=0.01。文中所用时间均为北京时。

4）大风发生概率的计算

计算两站间的气压差，并结合设定的大风阈值，统计气压差大于特定值时大风发生的小时数，计算该时间与气压差超过该特定值的总时长的比值，得到特定气压差条件下大风发生的概率。

气压作为风形成的指示器，对风速的变化具有直接影响，特别是在特殊地区的气象预报中，气压变化受到极大关注。以新田站和葫芦口大桥站的大风事件为例，分析气压变化特征及其与风速的关系。

新田站风速增加时气压显著下降，风力的大小和风速增加的时间与气压下降的幅度、气压波峰和波谷的时间密切相关。不同大风事件中，气压提前下降的时间有所不同，有的长达6~7 h，有的仅1~2 h。选择2020年1月7日和12月21日两次具有代表性的连续大风事件，研究峡谷区气压和风速变化的关系（图2）。2020年1月7日16：00—9日16：00，峡谷连续49 h出现大风，新田站8日09：00风速开始增加，5 h后风速为13.9 m·s^-1（7级），随后风速持续上升至8日19：00，达19.0 m·s^-1，之后风速开始下降；风速增大前，8日02：00气压峰值为901.9 hPa，经过7 h降到最低值894.5 hPa，下降7.4 hPa，气压开始下降时间比风速增大时间提前7 h，此现象也具有坝区大风天气的代表性。12月21日的大风事件中，22日08：00风速开始增加，5 h后达到7级，19：00风速达到23.2 m·s^-1的极大值，随后开始下降，其间风速连续18 h超过7级；风速增加前6 h，即22日02：00气压开始从907.4 hPa的峰值开始下降，8 h后降至最低值896.8 hPa，下降10.6 hPa，气压开始下降时间比风速增大时间提前6 h。

分析峡谷区两次大风事件发现风速与气压的变化相似，大风前气压均明显下降，但气压提前下降的时间差异较大。进一步研究大风发生前的最大气压差、风速增加时间与气压峰值时间差及风速增加到7级所需时间这3个参数与风速变化的关系，以期为大风预警提供参考。图3为新田站和葫芦口大桥站大风事件中3个参数的箱线图。可以看出，大风事件中，新田站最大气压差为6.6~11.0 hPa，其中75%的值高于7.4 hPa，中位数为8.3 hPa。这与新田站干季的平均气压日较差6.5 hPa相比，大风日变压幅度明显较大。葫芦口大桥站最大气压差为5.6~12.4 hPa，其中75%的值高于7.7 hPa，中位数为9.1 hPa，高于新田站，表明葫芦口大桥站大风前气压变化更为明显。两站大风日气压差的下四分位数分别为7.4、7.7 hPa，可将7.7 hPa定为坝区大风前的最低气压变化阈值，即当测站地面气压下降超过7.7 hPa时，大风发生的可能性增大。

进一步分析大风事件中，两站风速增加时间与气压峰值时间差。新田站其中位数为4 h，上、下四分位数分别为7、3 h，表明气压下降3~7 h后，风速开始增加；葫芦口大桥站其中位数也为4 h，上、下四分位数分别为6、2 h，葫芦口大桥站气压下降到风速增加的时间较短。两站中位数相同，表明两站大风事件中气压与风速变化过程在时间上具有相似特征。以新田站为参考，选取下四分位数3 h和葫芦口大桥站上四分位数6 h，以3~6 h为大风天气风速增加时间与气压峰值时间的时间差阈值，即气压连续下降3~6 h，风速开始增加的可能性增大。

新田站和葫芦口大桥站风速增加到7级所需时间的下四分数分别为3、1 h，表明风速有可能在极短时间内增大到7级；其上四分位数分别为7、6 h，表明多数情况下风速增长到7级需较长时间。综合考虑两站数据，以新田站发生最快的1 h和葫芦口大桥站的上四分位数6 h作为阈值，即当风速在1~6 h内持续增加时，峡谷区通常能达到7级以上大风。

通过分析峡谷区大风天气事件中风速与气压变化的关系发现大风发生前气压通常会明显下降，当气压下降超过7.7 hPa时，大风发生的可能性增大；此外，气压持续下降3~6 h以上时，风速开始增加的概率也相应增加；风速连续增加1~6 h后，出现7级以上大风的可能性较高。这3个阈值有助于预测风力等级及风力达到7级所需时间，可为坝区大风预警提供重要参考。

峡谷区大风前气压通常出现提前下降，表现为负变压。变压值也是预报业务中常用的物理量之一。分析风速增加前不同时间段的变压特征和3 h间隔变压值，以确定不同变压的阈值，从而提高大风灾害的预警效果。

统计新田站大风个例中风速增加前的变压值特征（表1）发现，在风速增加前的不同时段，负变压占比明显高于正变压，风速增加前8 h和9 h负变压的占比最高，达82%；3 h负变压占比最低（69%）。这表明峡谷地区大风时气压的持续下降特征非常明显，且气压稳定下降的时间越长，发生大风的可能性越高，这一发现与朱乾根等（2007）的研究相符，该研究指出气压局部变化可导致与风场相关的地转偏差，在这种情况下，地面的负变压中心区会引起变压风的辐合并引发上升运动，从而形成大风天气。此外，Charba（1974）、Droegemeier和Wilhelmson（1987）的研究也表明，在大风天气发生前，局地空气的上升运动会导致地面气压降低，形成异常变压。

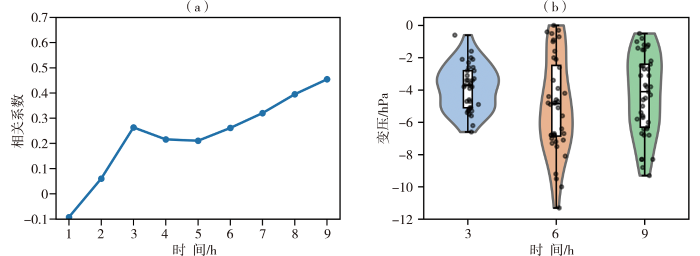
分析新田站大风事件中风速与不同时段变压的相关性[图4（a）]发现，新田站的风速除了与前1 h变压负相关外，其余均为正相关，这表明随着时间推移，负变压对大风的影响逐渐增强。比较风速与3、6、9 h变压的相关系数，发现与3 h和6 h变压的相关系数为0.26，与9 h变压的相关系数最高（0.45），均通过0.05的显著性检验。因此，变压值是大风预报的重要参数，特别是3、6、9 h变压值在大风预警中具有较好的效果，在业务中也得到广泛应用。分析新田站51个大风事件中3、6、9 h变压值的分布[图4（b）]发现，3 h变压值范围为-6.6~-0.6 hPa，其中位数附近样本相对最多，表明大风中3 h负变压稳定，与无大风的3 h变压明显不同。6 h变压值范围为-11.3~0 hPa，而9 h变压数据较均匀，这两个变压值的范围都明显大于3 h变压。以上分析表明，在大风天气中，地面3 h变压值相对稳定且集中，能够有效提取大风信息，对大风的预报有效性强。鉴于3 h负变压中超过96%的样本变压值大于2 hPa，将3 h负变压超过2 hPa作为变压阈值，以预警地面大风的发生。

风速变化是气流波动作用的结果，气流在波动中向前传播也是峡谷风速增强的原因。在重力内波发展过程中，空气微团的振动引发空气质量的辐合和辐散，并向四周传播，成为局地大风发生的重要机制（朱乾根等，2007）。金沙江下游的纵向峡谷地形限制气流主要以偏北和偏南的大风通过，其中以逆水流方向的偏北大风最为频繁（尹晔等，2023）。

上下游测站大风天气密切相关。以葫芦口大桥站、骑骡沟站和荒田站分别代表峡谷的上游、中段和下游，使用这3个站的逐分钟风速数据，以2022年2月9日—13日的连续大风事件为例，对比各站风速变化（图5），葫芦口大桥站风速最强，其次是荒田站，骑骡沟站风速最小，3站差异较大。葫芦口大桥站地形最狭窄，峡谷风效应下的风力最强；骑骡沟和荒田站地势较开阔，且靠近河沟，受大风气流影响较小，风速偏低。各站风速波动变化时，葫芦口大桥站先于骑骡沟和荒田站出现大风天气，且波峰较后两站提前较长时间。3个波峰的时间差均约8 h，这表明葫芦口大桥站易受上游气压变化影响，出现较中下游站点提前的峡谷大风天气。

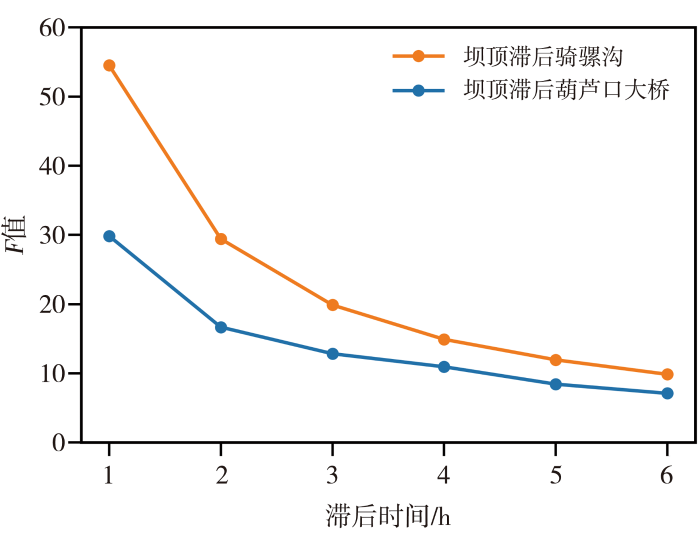
大风对水电站坝区的影响备受关注。以坝顶站为例，分析其在偏北大风影响下与上游葫芦口大桥和骑骡沟站风速峰值的时间关系。坝顶站与葫芦口大桥站的风速相关系数为0.72，与骑骡沟站的相关系数为0.64，且均通过0.05的显著性检验。为确定峡谷区大风发生时间的先后关系，采用格兰杰因果检验方法计算坝顶站与其他两站风速序列的关系。3站的极大风速序列均通过时间平稳性检验，呈现平稳变化特征。从图6的不同滞后时间曲线来看，坝顶站风速相对于葫芦口大桥站和骑骡沟站在滞后1 h时最高，F值分别为54.53和29.85，这表明坝顶站大风最有可能滞后于葫芦口大桥站和骑骡沟站1 h发生。随着滞后时间的增加，F值迅速减小，在6 h后降低至10左右。在所有滞后时间中，F值对应的P值均远小于预设的显著性水平，表明格兰杰因果关系的显著性通过检验，即上游站点（葫芦口大桥站和骑骡沟站）的大风事件早于下游坝顶站发生，且骑骡沟站风速增加的预测效果更佳，这对峡谷区大风预警有一定指示作用。

综上，峡谷区上游的葫芦口大桥站和骑骡沟站的大风通常比坝顶站提前1 h出现，表明在上游站点观测到大风后1~2 h，峡谷中下游地区遭遇极端大风的可能性最大。这一时间段是大风事件最易发生时段，对大风预警提供了重要参考。

气压差是局地气压梯度力的重要决定因素，也是大风形成的关键驱动力。在峡谷地形区，上下游测站的气压差决定了大风的强度和发生概率。为研究气压差在大风预警中的作用，分析新田站2 min平均风速与骑骡沟站、荒田站气压差以及葫芦口大桥站、荒田站气压差的关系，相关系数分别为0.55、0.70，且均通过0.05的显著性检验，表明风速与上下游气压差存在密切关系。

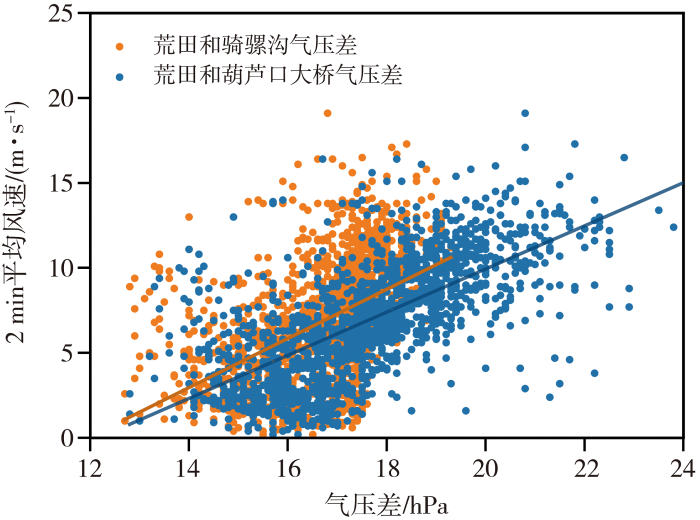
由新田站2 min平均风速与各站气压差的散点图（图7）可知，新田站风速与上下游气压差存在一定正相关关系，随着气压差增大，新田站风速增强。此外，荒田站和葫芦口大桥站的气压差整体大于和骑骡沟站的气压差，且前者与新田站风速的拟合线斜率较小，表明在相同气压差下，新田站的风速更容易受荒田和骑骡沟站气压差的影响。同时荒田站和骑骡沟站的气压差分布较为分散，风速波动更剧烈，而荒田站和葫芦口大桥站的气压差分布相对集中，对风速的影响较为稳定。

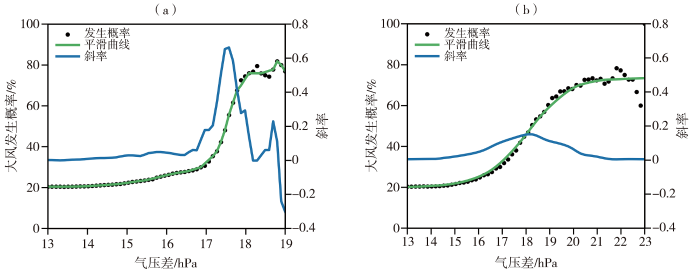
以10 m·s^-1为大风阈值，通过分析上下游站点的气压差确定峡谷区大风事件的发生概率。使用平滑滤波算法拟合大风发生概率的变化趋势（张贤亮等，2019），以捕捉气压差影响风速的敏感性；计算拟合曲线斜率的极值点用于确定气压差的阈值。如图8所示，荒田站和骑骡沟站气压差的阈值为17.6 hPa，荒田站和葫芦口大桥站的气压差阈值为18.1 hPa，当气压差大于上述阈值时，坝区大风发生的概率明显增加。特别是葫芦口大桥站和荒田站分别位于峡谷最上游和最下游，其气压差能全面反映整个峡谷气压梯度场的变化，准确反映风速响应气压扰动的剧烈波动，因此以18.1 hPa作为气压差阈值，能最大程度地反映峡谷压力场变化，有助于提高预警的准确率和可靠性。

根据对峡谷地区大风天气各气象参数的分析，以新田站为例对各参数阈值的适用性进行检验。新田站2023年1月共记录了9次大风事件，结果如表2所示。

1）最大气压差

9次大风事件中，5次最大气压差超过7.7 hPa，分别为8.7、9.5、12.5、8.6、14.9 hPa；3次最大气压差接近7.7 hPa，分别为7.3、7.2、7.5 hPa；仅有1次最大气压差为5.4 hPa，低于阈值。此外，6次大风事件中风速增加时间与气压峰值时间差为3~6 h；8次大风事件中风速增加到7级所需时间为1~6 h。因此分别选择7.7 hPa、3~6 h和1~6 h作为最大气压差、风速增加时间与气压峰值时间差和风速增加到7级所需时间的阈值。

2） 3 h变压预警大风的阈值检验

9次大风事件中，2次为较弱的3 h正变压；7次为3 h负变压，其中5次超过2 hPa，其余2次负变压也较弱。因此将3 h负变压超过2 hPa作为峡谷区大风预警参数，可有效识别峡谷区大风天气。

3）上游测站与坝区风速变化的关系

9次大风事件中，有4次骑骡沟站的风速峰值比新田站提前，其中3次提前1~2 h；其余5次葫芦口大桥站的风速峰值比新田站提前（4次提前1~2 h）。总体而言，上游测站的大风出现时间普遍比下游略早，提前1~2 h的预警效果较好。此外，分析发现9次大风事件中，有6次葫芦口大桥站和荒田站的气压差超过18.1 hPa的阈值。这表明，当上下游气压差大于18.1 hPa时，坝区大风发生的概率明显增加。

若以表2中7个参数同时满足阈值条件来预警大风，9次事件中仅有1次能够准确预警；若要求满足6个以上参数来预警大风，则可准确预警3次；若要求满足4个以上参数来预警大风，可准确预警6次。峡谷区大风频繁，建议以满足4个以上参数作为判识条件，进行大风天气预警，以获得较好的预报效果。

本文基于干季金沙江下游峡谷地形区的大风事件，采用多种数据分析方法和格兰杰因果检验，研究大风天气过程中气压和风速的关系，讨论气压对大风的影响及对大风预警的效果，得出以下主要结论。

1）分析坝区峡谷风速与气压的关系，发现不同测站风速与气压变化相似，表现为大风前气压连续明显下降。新田站大风前气压下降6.6~11.0 hPa，高于干季平均气压日较差（6.5 hPa）；气压下降超过7.7 hPa时，通常会有大风出现；且气压连续下降3~6 h后，风速开始上升，风速继续增加1~6 h后通常会达到7级以上风力。7.7 hPa（最大气压差）、3~6 h（风速增加时间与气压峰值时间差）、1~6 h（风速增加到7级所需时间）3个阈值有助于判定风力等级及预测风力达到7级的时间，可为坝区大风预警提供重要参考。

2）金沙江峡谷大风事件中地面通常为负变压，其中3 h变压在大风事件中最为有效和稳定；当坝区3 h负变压超过2 hPa时，大风发生的概率明显增加。

3）受峡谷风效应影响，上下游测站大风发生时间存在差异。格兰杰因果关系检验表明，葫芦口大桥站和骑骡沟站大风通常较坝顶站提前1 h。此外，当荒站田和葫芦口大桥站的气压差超过18.1 hPa时，峡谷区气压梯度增强，易引起坝区大风。

本文结合峡谷区特殊地形与大风预警的业务经验，研究地面气象要素变化预警大风的方法，确定了7个有效预警参数。当气压场满足这些条件时，大风发生的概率明显增加，可为大风灾害预警提供重要信息。尽管这些信息对大风预警有一定作用，但峡谷区大风形成机制复杂且影响因素繁多，使得检验时效有限，构建的参数不能完全解决大风预警的难题。需要在更多个例检验的基础上订正阈值，以提高其在大风预警中的适用性。