0 引言
现有的风功率预测技术主要有物理方法、统计方法、机器学习方法。其中,物理方法(张铁军等,2011;许沛华等,2021)以数值模式为基础,通过预测未来风速、风向,结合风电机组的“风速-功率”曲线得到未来的风功率预测值,然而风速、风向预测必然存在一定的误差,这个误差通过“风速-功率”曲线会得到传递,另外数值天气预报更新速度相对较慢,因此,物理方法更加适合风功率的中短期预测。统计方法主要根据风功率历史数据建立统计学习模型对未来的风功率进行预测,如自回归(Erdem and Shi, 2011)和自回归移动平均(邹金等,2019;赵征和汪向硕,2020),这种方法简单,但是风功率预测往往涉及大量的历史数据,且历史数据对预测值影响很大,历史数据量不足会使预测结果不够精准。机器学习方法正处于高速发展之中,其强大的非线性映射能力使其能从历史数据学习特定的映射关系,并有极强的自我修正功能,是近年来风功率的主流预测方法(Cao et al.,2019)。基于神经网络的深度学习模型是应用最广泛的一种机器学习方法,如卷积神经网络(Convolutional Neural Network,CNN)(Wang et al.,2018)、深度置信神经网络、长短期记忆网络(Long Short-term Memory,LSTM)(贾睿等,2022;谷学静等,2023;申艳杰和尚兆晖,2023;宋江涛等,2023)、门限循环网络(Gated Recurrent Unit,GRU)(Niu et al.,2020;王雨城,2020),决策树模型、K近邻(K-Nearest Neighbor,KNN)模型以及梯度提升决策树、装袋算法等集成算法(李国和江晓东,2018;杨秀媛等,2018;梁涛等,2020)在超短期风功率预测中也得到一定应用,但使用相对较少。已有研究一方面通过多种算法的组合来提高预测性能,如Liu等(2018)基于小波包分解(Wavelet Packet Decomposition,WPD)、CNN和LSTM网络的深度学习模型,建立了多种模型融合的风功率组合预测方法;Hong和 Rioflorido(2019)釆用CNN和以双高斯函数(Double Gaussian Function, DGF)作为激活函数的径向基神经网络(Radial Basis Function Neural Network,RBFNN)建立组合预测模型对风功率进行预测。另一方面,通过参数优化算法的改进从而提高模型的预测性能,如丁家乐等(2019)使用改进的萤火虫算法优化了回声状态网络(Echo State Network,ESN)权值的计算,王雨城(2020)提出一种改进的混合蚱蜢优化算法优化了CGRU(CNN结合GRU)的网络参数,研究表明改进的参数优化算法提高了模型的预测精度。
完全预报(Prefect Prognostic,PP)法是数值预报产品解释应用中成熟的方法(牟银杰,2003;蔡义勇等,2006),使用该方法需要建立同时刻预测因子与预测要素的“真”函数关系模型,其优点是所建立的关系模型不依赖于具体的数值产品,而且随着数值模式预测精度的提高,对风功率的预测精度也会随之提高。在实际应用中,将不同预报时效(如短期、超短期)的数值预报结果代入模型中,便可得到相应时效的风功率预测产品。利用PP法进行风功率预测的一个关键步骤就是建立同时刻预测因子与风功率间可靠的预测模型。在超短期、短期、中长期等不同时间尺度的风功率预测领域,机器学习模型尤其是组合模型应用十分广泛。而通过近几十年的发展,机器学习算法繁多,如何选择可靠有效的单一模型以及如何契合、关联不同模型是多模型组合预测方法的重点和难点。本文基于KNN、引导聚集算法(Bootstrap Aggregating,BA)、梯度提升决策树(Gradient Boosting Decision Tree,GBDT)、自适应提升树算法(Adaptive Boosting,AB)、多层感知机(Multilayer Perceptron, MLP)、CNN等几种典型的机器学习算法,根据KNN、BA、CNN在测试集上表现出的特点,研究KNN、BA与CNN的组合方法,建立融合KNN、BA与CNN的同时刻风功率预测模型,以期为利用PP法进行风功率预测提供支撑。
1 数据及方法
1.1 数据
使用2020年1月1日—12月31日甘肃酒泉中广核干东风电场的风功率及相同时刻的10 m、30 m、50 m、70 m高度风速、风向及气温、气压、湿度等观测数据,观测间隔为15 min,共有35 136条数据。为了提高数据的可靠性,首先对原始数据进行数据清洗,将原始数据集中的缺测值设为无效值(包括185条,占比约0.53%),另外使用3倍标准差方法将超过±3倍标准差的数据设置为无效值(包括1 003条数据,占比约2.90%),无效值用前后若干数据的平均值替换。然后对原始数据集进行划分,通过固定的随机数种子选择其中80%的数据作为训练集进行模型训练,20%的数据作为测试集用于模型验证。
1.2 机器学习方法
1)KNN算法
KNN算法(Cover and Hart, 1967)原理:存在一个样本数据集合x,比较x与
式中:di和dj为样本特征向量;p为特征项向量空间的维数;
2)BA算法
该算法又称装袋算法(Breiman, 1996),是机器学习领域的一种团体学习算法。它的原理是同时构建多个弱学习器,最终将多个弱学习器进行组合形成一个强学习器。该算法采用Bootstrap采样方法,从原始样本中进行有放回的采样方法提取多个样本集,利用每个样本集训练一个学习器,多个学习器预测结果结合起来作为最终预测值,在回归问题中将多个预测均值作为最终的预测值。在装袋算法中每个学习器之间相互独立。本文选择决策树为装袋算法的基学习器。
3)GBDT算法
GBDT(Friedman,2001)是一种基于回归树的算法,对回归树进行梯度提升,提升回归树采用加法模型对最终模型做组合,其采用前向分布算法拟合一系列回归树,即在回归树模型的构建过程中,每一个回归树模型都是通过学习前一个回归树残差的负梯度后调整权重得到。提升回归树数学模型如下:
式中:M为所建立的回归树数量;
4)AB算法
AB算法(Freund and Schapire,1997)中建立了多个一个点两个叶子结构的树模型,与GBDT不同,AB算法中每个树模型的创造是基于前一个树模型的误差,更加关注前一个树模型误差较大的数据,为下一个树模型产生训练样本,进而达到降低集合模型误差的效果。
5)MLP
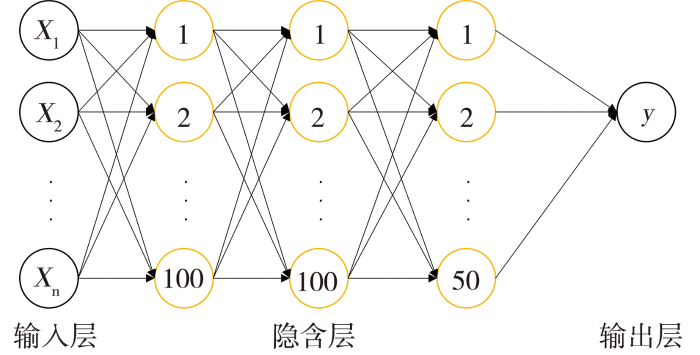
MLP(Rumelhart,1986)是最简单的深度神经网络,包括输入层、隐含层和输出层,它是一种全连接的神经网络,输入层、隐含层、输出层的隐射关系如下:
式中:X表示输入变量;H表示隐含层变量;O为输出变量;
图1
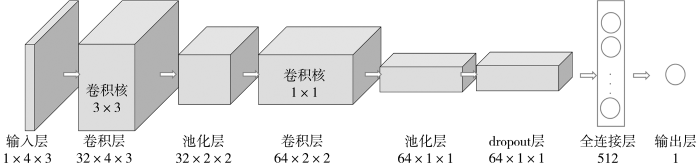
6)CNN
图2
1.3 机器学习的融合方法
1)A+B型融合
将A模型的输出结果作为一个新的特征结合风速、风向、气温、气压等基础特征再输入到B模型中进行模型训练。
2)CNN组合模型
将若干单一模型的输出结果作为新的特征结合风速、风向、气温、气压等基础特征再进行CNN模型的训练。
1.4 模型评价指标
利用均方根误差(Root Mean Squared Error,RMSE)对所建立的各个机器学习模型的预测结果进行衡量,均方根误差越小,说明预测结果越准确,其计算公式如下:
式中:n为所有测试样本的数量;
2 风功率计算模型构建
2.1 风功率与各气象要素的关系
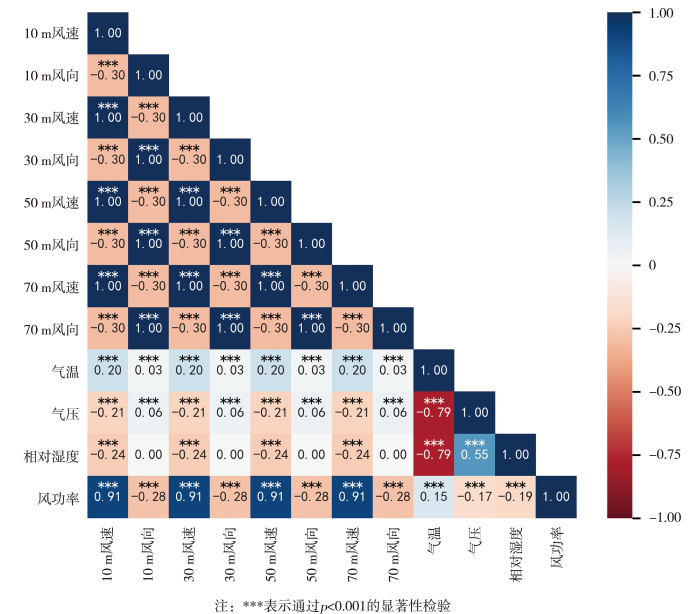
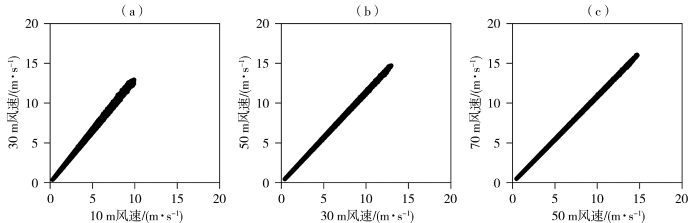
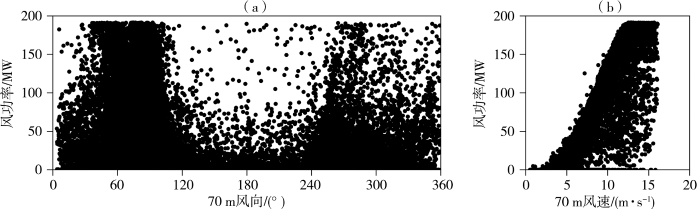
为了提炼主要的预测因子,首先计算风功率和不同高度风速、风向、气压及气温等要素的相关系数(图3),可以看到风功率和各层风速的相关系数均在0.90以上,相关性非常显著(p<0.001),且高度越高,相关系数越大,70 m风速与风功率相关系数最大(0.91)。不同高度层风速、风向有很强的相关性,相关系数接近1.00(高层风速间相关性高于低层,如图4所示);风向、气压、气温、相对湿度与风功率也显著相关,风向与风功率的关系呈现出“U”型[图5(a)],风机发电的主要风向为40°~100°,在250°~300°风向发电功率稍弱,120°~220°风向风机发电功率最弱。绝大部分数据符合“风速-功率”曲线(杨秀媛等,2018),但有相当数量的数据并不符合这一曲线,利用“风速-功率”曲线无法准确预测该部分数据[图5(b)]。
图3
图4
图4
不同高度层风速之间的关系
(a)10 m与30 m,(b)30 m与50 m,(c)50 m与70 m
Fig.4
The relationship between wind speeds at different levels
(a) 10 m and 30 m,(b) 30 m and 50 m,(c) 50 m and 70 m
图5
图5
70 m高度层风向(a)及风速(b)与风功率的关系
Fig.5
Relationship between wind direction (a), wind speed (b) and wind power at the height of 70 m
2.2 单一风功率模型的预测效果对比
通过对比发现,高层风速与风功率的相关关系略好于低层风速,为了消除共线变量对模型的影响,故选择70 m风向及风速、气压、温度、相对湿度等要素拟合风功率。各种算法在训练集和测试集上的拟合R2和RMSE如表1所示。
表1 各种机器学习算法模型在训练集和测试集上的拟合效果
Tab.1
| 模型 | 训练集 | 测试集 | ||
|---|---|---|---|---|
| RMSE/MW | R2 | RMSE/MW | R2 | |
| KNN | 12.92 | 0.93 | 17.21 | 0.88 |
| GBDT | 13.39 | 0.93 | 15.32 | 0.90 |
| AB | 17.54 | 0.87 | 18.57 | 0.86 |
| BA | 4.73 | 0.99 | 13.08 | 0.93 |
| MLP | 16.33 | 0.89 | 17.00 | 0.88 |
| CNN | 14.37 | 0.91 | 15.19 | 0.90 |
注:相关性均通过p<0.001的显著性检验,下同。
图6
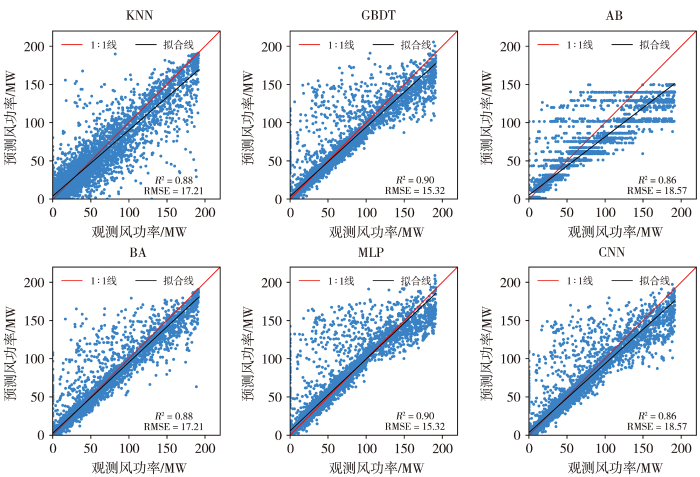
图6
各模型在测试集上实际风功率和预测风功率的散点图
Fig.6
Scatter plots of actual wind power and predicted wind power for each model on test data
图7
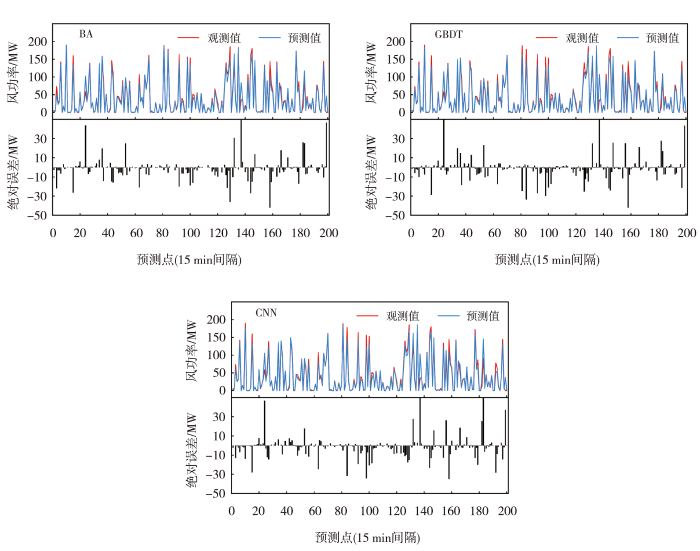
图7
BA、GDBT、CNN模型在部分测试集数据上的折线图
Fig.7
Line charts of BA, GDBT, CNN models on partial test set data
2.3 组合模型的预测效果
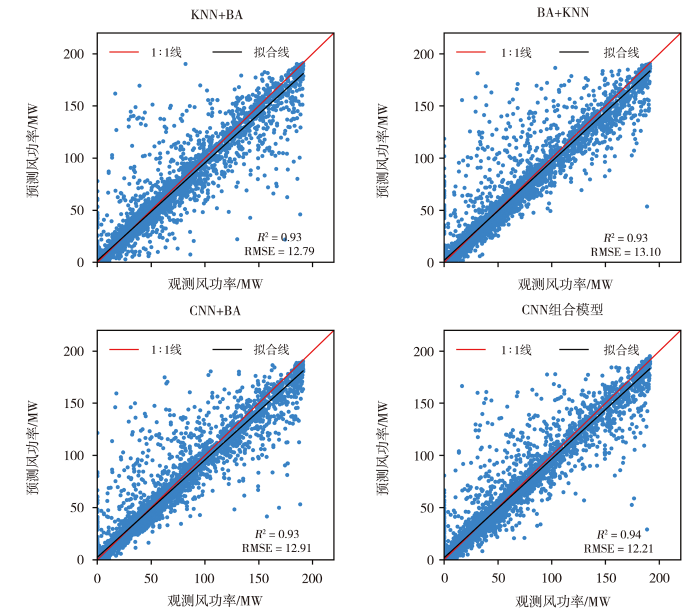
首先,在前面的分析中注意到KNN模型虽然拟合效果较差,但是模型拟合值异常偏大的情况较少,同时存在一些异常偏低的预测值,BA和CNN是效果较好的两种模型,故将KNN和BA、CNN和BA进行A+B型的组合。其次,将KNN模型、BA模型、KNN+BA模型和BA+KNN模型的输出结果作为新的特征结合风速、风向、气温、气压等基础特征进行CNN组合模型的训练。各种组合模型在训练集和测试集上的拟合R2和RMSE如表2所示,组合后的模型在测试集上的拟合散点图、部分验证数据的折线图见图8-9。对比图6、8发现,这几种模型的误差都比单一模型有所降低,其种KNN+BA模型对BA模型预测值异常偏大的缺点有一定的矫正,但与KNN模型特点一致,也出现部分高值拟合偏低的情况;BA+KNN模型与BA模型一样存在较多的低值高估情况,并没有发挥出KNN模型的优势;CNN+BA模型存在高值区拟合偏低的趋势;CNN组合模型的误差最低,RMSE为12.21 MW,比单一模型中最好的BA模型误差下降了约6.7%,且CNN组合模型对CNN单一模型高值低估、低值高估和BA模型低值高估的情况有所改善。
表2 组合模型在训练集和测试集上的拟合效果
Tab.2
| 模型 | 训练集 | 测试集 | ||
|---|---|---|---|---|
| RMSE/MW | R2 | RMSE/MW | R2 | |
| KNN+BA | 3.73 | 0.99 | 12.79 | 0.93 |
| BA+KNN | 3.32 | 0.99 | 13.10 | 0.93 |
| CNN+BA | 4.38 | 0.99 | 12.91 | 0.93 |
| CNN组合模型 | 3.68 | 0.99 | 12.21 | 0.94 |
图8
图8
组合模型在测试集数据上的拟合散点图
Fig.8
Scatter plots of actual wind power and predicted wind power for combined models on test data
图9
图9
KNN+BA、BA+KNN、CNN+BA、CNN组合模型在部分测试集数据上的折线图
Fig.9
Line charts of KNN+BA, BA+KNN, CNN+BA, CNN combined model on partial test set data
3 讨论
本文研究结果与Liu等(2018)和Hong和Rioflorido(2019)研究结果一致,通过组合多个机器学习算法可以明显提高风功率的预测精度。虽然单个机器学习模型精度相对较低,但单一模型预测的风功率与实际风功率的R2相较风速与风功率的R2得到明显提高,因此将关系更好的多个单一模型预测结果作为新的特征进行CNN模型训练能够进一步提高风功率的预测精度。风功率的物理预测方法以“风速-功率”曲线关系为基础,将数值模式风速的预测值代入到“风速-功率”关系中实现风功率的预测。与物理方法思路相近,PP法以同时刻预测因子与风功率的模型为基础,将数值模式中预测因子的预测值带入模型实现了风功率的预测。从图5(b)中明显看到,有相当数量的数据并不符合“风速-功率”曲线关系,这导致风速与风功率的R2大约为0.80,而CNN组合模型R2提高到0.94。基于CNN组合模型的PP法可能给利用数值模式风功率预测精度的提高带来新的契机,但因为CNN组合模型除了风速外还需要数值模式输出的风向、气温、相对湿度等多个气象因子的预测值,PP法是否能切实提高基于数值模式的风功率预测精度还有待进一步研究。然而本文在划分训练集和测试集时使用了随机种子来保证得到每次程序运行或者每个模型都使用了相同的训练集和测试集,从而使每个模型或者每次参数调优的结果具有可比性,尽管使用了结果相对好的随机种子,但这仍然是基于一次随机选择的训练集展开的,这使结果存在一定的不确定性。
4 结论
利用2020年1月1日—12月31日甘肃酒泉中广核干东风电场的风功率及风塔风速数据,基于多种典型的机器学习算法和单一模型在测试集上表现出的特点,研究KNN、BA与CNN的组合方法,建立融合KNN、BA与CNN的风电功率预测模型,得到如下具体结论。
1)通过多种机器学习模型的对比发现,文中所使用的单一模型均对风功率部分值存在低值高估情况,仅使用气象要素的CNN单一模型还存在高值低估情况,这些模型中BA算法预测精度最高。
2)组合模型均能在一定程度上提高单一模型的预测精度,其中CNN组合模型在测试集上的均方根误差为12.21 MW,比单一模型中最好的BA模型下降约6.7%,CNN组合模型可以明显改善CNN单一模型高值低估、低值高估和BA模型低值高估的情况。
参考文献
Bagging predictors
[J].
Prediction of wind power generation base on neural network in consideration of the fault time
[J].
Nearest neighbor pattern classification
[J].
ARMA based approaches for forecasting the tuple of wind speed and direction
[J].
A decision-theoretic generalization of on-line learning and an application to boosting
[J].
Greedy function approximation: A gradient boosting machine
[J].
A hybrid deep learning-based neural network for 24-h ahead wind power forecasting
[J].
Gradient-based learning applied to document recognition
[J].
Smart deep learning based wind speed prediction model using wavelet packet decomposition, convolutional neural network and convolutional long short term memory network
[J].
Wind power forecasting using attention-based gated recurrent unit network
[J].
Learning representations by back propagating errors
[J].
Deep belief network based k-means cluster approach for short-term wind power forecasting
[J].