0 引言
通过洪水调查和计算设计暴雨,可以分析洪水要素与洪水预警指标(如转移雨量)之间的关系,从而为快速、准确地预报洪水灾害提供理论支持(苏军锋等,2021;铁永波等,2022;肖贻青等,2023)。洪水调查主要依赖人工经验和简单的观测数据,随着技术手段的进步,目前可以借助气象、水文和遥感技术,进行精准、全面的调查分析,从而建立多种洪水模型,用于模拟不同洪水事件的发生过程(丁文杰,2021;秦军等,2022;Tan et al., 2024)。然而,由于气候和地形条件的复杂性,这些模型在预测极端洪水事件时存在较大的误差(梁述杰,2005;段志勇,2015;沙宏娥等,2022)。如陈学林等(2012)提出了一种综合的洪水预报模型,考虑了地质、气象和水文等多方面因素,但由于对数据完整性要求较高,模型应用存在一定的局限性;肖贻青等(2023)利用遥感技术对未监测流域的短时洪水预测进行研究,但由于缺乏长期观测数据,限制了模型的准确性和稳定性;张华兴等(2013)采用概率模型评估复杂河流流域的洪水风险,但由于数据不完整,洪水模型在中小流域的洪水预测方面仍有待改进。
综上所述,尽管中小流域洪水要素特征的调查和预警雨量的研究已有一定进展,但仍存在诸多不足。数据支持对洪水调查与预测至关重要,但由于洪水调查的复杂性,许多地区缺乏完整的实时数据(王盛萍等,2006;Jin et al., 2015; Wang et al., 2020)。尤其在干旱半干旱地区,由于地理和资源限制,洪水调查的时间跨度和数据深度受限(Chen et al., 2023)。此外,现有洪水模型在应对复杂地理和气象条件(如西北干旱半干旱地区)时,预测的准确性仍有待提高。因此,本文选取甘肃省永昌县(位于干旱区)和夏河县(位于半干旱区)作为研究对象,基于全国山洪灾害防治项目组提供的调查数据、工作底图和基础资料。通过收集整理夏河县34个小流域和永昌县240个过水断面的地形地貌特征因子,采用经验和理论模型计算各单元的山洪暴发临界雨量、汇流时间及不同重现期的设计洪水,并对整个区域的洪水要素进行统计插值分析。最后,分别对各研究区的洪水要素与预警因子进行相关性分析,以确定影响洪水特征的控制因素,并比较不同研究区之间的异同。此外,采用机器学习方法构建洪水预警指标的统计经验模型。为评价新回归模型的合理性,采用新模型对甘肃省合作市34个调查流域的预警降雨量进行计算,并对结果进行分析。本研究为深入理解洪水控制因素提供了理论依据,并为中小流域的快速洪水预报提供了支持。
1 研究区、资料及方法
1.1 研究区概况
考虑气候、地形、降水和数据完整性等因素,选取甘肃省永昌县和夏河县作为研究对象。这两个区域在坡度和降雨特征上存在明显差异,为分析不同地形和降雨条件下的洪水特征提供了良好的基础。同时,两个区域的调查数据较为完整,便于深入分析洪水要素之间的关系,建立精准的预报模型。
图1
图1
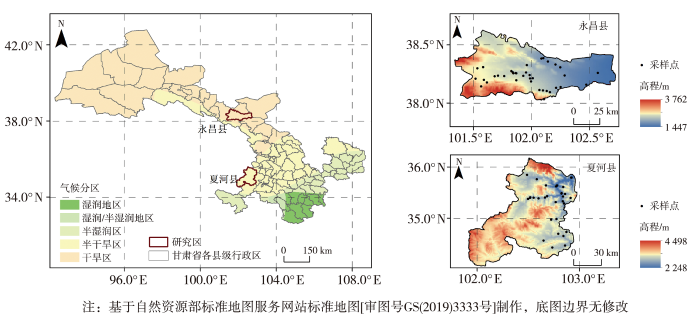
研究区地理位置及数据采集点空间分布
Fig.1
Geographical location of the study area and the spatial distribution of data acquisition points
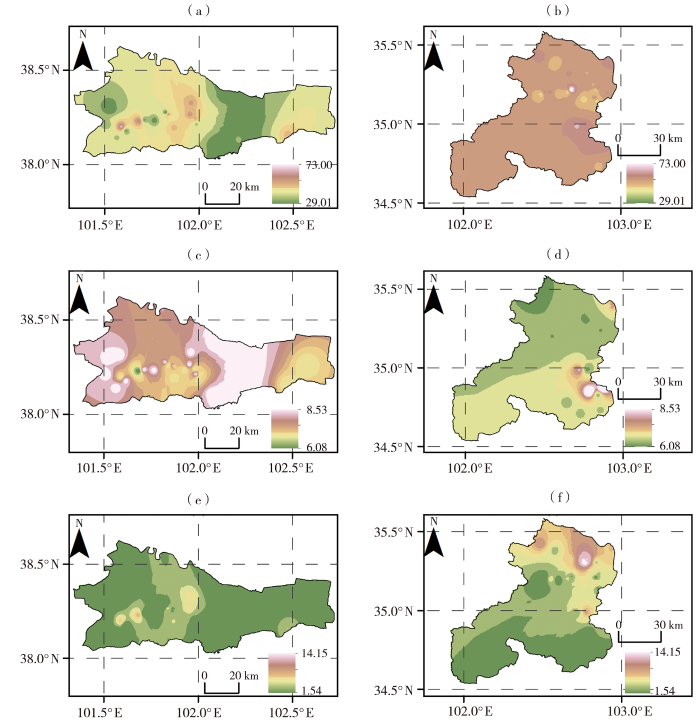
永昌县的坡度均小于10°,主要沟道分布在县城的东西两端,大部分沟长为30~40 km,且沟道比降呈现出东小西大的特征;相比之下,夏河县的地形较为复杂,东北部坡度变化较大,而西南部则相对平缓(图2)。
图2
图2
永昌县(a、c、e)及夏河县(b、d、f)坡度(a、b)(单位:°)、主沟道长度(c、d)(单位:km)及主沟比降(e、f)(单位:‰)空间分布
Fig.2
The slope angle (a, b)(Unit: °), length of main channel (c, d)(Unit: km) and slope gradient of main channels (e, f)(Unit: ‰) of Yongchang (a, c, e) and Xiahe (b, d, f) County
1.2 数据来源
本文以全国防洪基础数据①②(①全国山洪灾害防治项目组.《山洪灾害分析评价技术要求》,2014. ②全国山洪灾害防治项目组.《山洪灾害分析评价方法指南》,2015.)为依据,工作底图包括主要要素的数字线画图、数字正射影像遥感信息、小流域土地利用和植被类型信息,较为全面地反映山丘区小流域地表信息;小流域基础属性数据反映了现阶段技术条件下小流域的地形地貌、几何特性及一定的水文学特征。降水量资料采用甘肃历史多年平均暴雨量等值线图(甘肃省水文水资源勘测局,2003)。考虑到小流域汇水区的完整性和县级行政区的一致性,采用GIS软件工具对整个研究区进行校正。并通过对研究区内的重点流域现场调查、河道测量和实地走访,得到研究区内的河道参数信息③④(③全国山洪灾害防治项目组.《山洪灾害调查评价基础数据处理技术要求》,2013. ④全国山洪灾害防治项目组.《山洪灾害调查工作底图制作技术要求》,2013.),以及历史洪水信息⑤(⑤全国山洪灾害防治项目组.《山洪灾害调查评价小流域划分及基础属性提取技术要求》,2013.),为计算结果校正提供数据支持。表1列出永昌县和夏河县野外调查信息。
表1 永昌县和夏河县野外调查信息
Tab.1
| 研究区 | 小流域山洪灾害分析评价范围/km2 | 乡镇/个 | 行政村/个 | 自然村/个 | 流域(断面)/个 | 调查 时间 |
|---|---|---|---|---|---|---|
| 永昌县 | 1 812.52 | 10 | 66 | 395 | 240 | 2014年 |
| 夏河县 | 1 709.99 | 11 | 34 | 86 | 34 | 2015年 |
为满足机器学习方法对数据量的要求,本文对调查的洪水要素及流域内基本地形特征采用克里金(Kriging)方法进行插值(Oliver and Webster, 1990),栅格大小设为1 km×1 km。同时,为了分析栅格大小对插值结果的影响,亦采用了2 km×2 km的栅格进行插值。对比两种栅格的插值结果后发现,不同栅格大小下的总体特征差异较小。最终,为满足数据量要求,选用1 km×1 km栅格的插值结果。插值后,夏河县和永昌县分别获得了10 420组和10 417组洪水调查数据(插值过程中进行了数据优化,因此一些变异性较大的数据未被纳入考虑范围),满足机器学习对数据量的要求。
1.3 洪水计算
洪水计算主要包括降雨和产汇流,根据现有水文资料和甘肃省现行的水文计算方法,分段确定计算方法。通过计算标准历时和汇流时间内的洪水特征要素,根据小流域内防灾对象的特征及土壤含水量特征,计算对应的雨量和水位预警值,从而确定准备转移和立即转移预警指标。
1.3.1 设计暴雨计算
针对缺少实测洪水记录的情况,设计暴雨的计算主要依据历史资料插值得来的暴雨图集和手册等资料,计算不同重现期下的降雨量,从而确定设计洪水和预警雨量。设计暴雨的输入参数主要包括对应频率和时段下的偏态系数、变差系数、折减系数及流域形状校正系数。
1.3.2 设计暴雨量计算
1.3.3 汇流时间分析
当流域面积小于等于100 km2时,选用“铁一院”法及经验公式法进行设计洪水计算,当流域面积大于100 km2时,选用瞬时单位线法及经验公式法进行设计洪水计算,具体计算公式参考《山洪灾害分析评价方法指南》。
1.3.4 暴雨时程分配计算
暴雨时程分配按《甘肃省暴雨洪水图集》(甘肃省水利厅, 1988)⑥(⑥甘肃省水利厅.《甘肃省暴雨洪水图集》,1988.)中各暴雨分区“综合概化雨型表”按雨峰所在相应时段比例设置,计算所得总雨量按比例分配得到暴雨时程。以100 a重现期降雨量为总雨量,由于流域面积较小(小于100 km2),暴雨时程分配以1、3、6、24 h雨量为控制时段,然后以各历时的同频率设计面雨量为控制进行放大,求得设计面雨量的时程分配。本文选取的代表雨量为3 h降雨量。
1.3.5 设计洪水计算
设计洪水的计算主要基于典型频率洪水和水位流量关系曲线。根据研究区现场调查成果及现行设计洪水计算方法,采用“铁一院”法、经验公式法及瞬时单位线法计算,从安全角度考虑,选用相对较大的设计洪水量作为设计洪水成果。
1.3.6 临界雨量计算
临界雨量是表征山区洪涝灾害发生的一个阈值,一旦降雨量超过这个阈值,就可能引发小流域山洪灾害,这一阈值被称为临界降雨量,通常以单位时间内(如1 h)的降雨量表示,有时也用几小时的降雨量表示。当降雨量超过该阈值时,地表径流汇流量刚好达到河道的排洪能力。本文采用试算法计算临界雨量(王继尧, 2019)。与临界雨量对应的预警指标之一是“准备转移雨量”,当降雨达到该值时,应密切监测雨量并随时做好居民转移的准备。另一个预警指标是“立刻转移雨量”,一旦达到该值,山洪灾害发生的可能性极大,需立即组织居民转移。基于安全考虑,本次机器学习模型中选用“准备转移雨量”作为预警指标。
1.4 机器学习结果数据分析
为表征不同指标之间的相关性,引入皮尔逊相关系数(Lee and Nicewander, 1988),相关系数接近1,表明两个参数之间存在较强的正相关关系;相反,若相关系数为-1,则表示两个参数之间存在负相关关系。
2 暴雨和洪水特征
2.1 暴雨
图3
图3
永昌县(a、c、e)和夏河县(b、d、f)100 a重现期降水量(a、b)(单位:mm)、暴雨时程分配(c、d)(单位:mm)及汇流时间(e、f)(单位:h)空间分布
Fig.3
The spatial distribution of precipitation (a, b)(Unit: mm), rainfall during storms (c, d)(Unit: mm) and convergence time (e, f)(Unit: h) in 100 a return period in Yongchang (a, c, e) and Xiahe (b, d, f) County
夏河县5 a、10 a、20 a、50 a、100 a重现期的降雨量分别为43~46 mm、52~55 mm、61~64 mm、65~68 mm、69~73 mm。夏河县同一重现期内的降雨区域差异较小,整体处于同一降雨带。通过分析34个计算单元的降雨特征发现,该区域山洪的降雨历时较短,雨强较大,且降雨主要集中在河道上游。虽然汇流面积较小,但沟道陡峭,导致对应洪峰模数较大。插值结果表明,夏河县的降雨量较为均匀且整体偏大[图3(b)]。暴雨时程分配呈现出西北部偏小、东南部偏大的特征,与流域地形特征高度相关[图3(d)]。而汇流时间则表现为相反的特征,东北部的汇流时间较长,西南部则较短[图3(f)]。
2.2 洪水
图4
图4
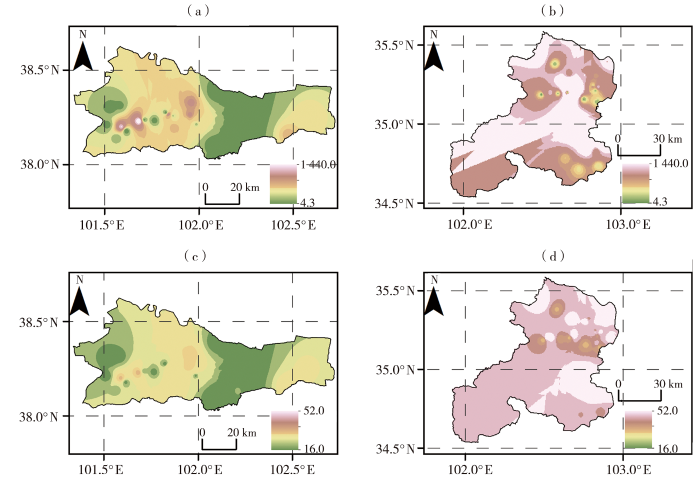
永昌县(a、c)、夏河县(b、d)洪峰流量(a、b)(单位:m³·s-1)和临界雨量(c、d)(单位:mm)空间分布
Fig.4
The spatial distribution of peak discharge rate (a, b)(Unit: m³·s-1) and critical rainfall (c, d)(Unit: mm) in Yongchang (a, c) and Xiahe (b, d) County
2.3 预警指标
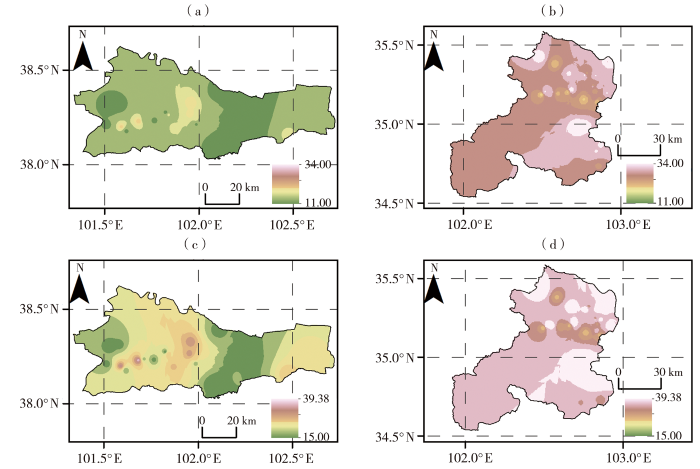
针对不同土壤含水量条件(较干、一般、较湿)计算相应的洪水预警指标,并对各计算单元的预警值进行统计分析(图5)。整体来看,永昌县的准备转移雨量为11~19 mm,立即转移雨量为15~30 mm,表现出东西两端阈值较大、中部较小的趋势。夏河县的整体预警阈值较大,其中准备转移雨量为25~34 mm,立即转移雨量为30~39 mm,西北部和东南部阈值较高,中部较低,且这一分布与地形特征存在一定的相关性。
图5
图5
永昌县(a、c)、夏河县(b、d)准备转移雨量(a、b)和立即转移雨量(c、d)空间分布(单位:mm)
Fig.5
The spatial distribution of prepared transfer rainfall (a, b) and immediate transfer rainfall (c, d) for Yongchang (a, c) and Xiahe (b, d) County (Unit: mm)
对比类似地区,甘肃舟曲地区典型村落的准备转移雨量和立即转移雨量分别为35~40 mm和48~55 mm(王继尧,2019),明显大于夏河县和永昌县的预警雨量,说明夏河县和永昌县的洪水对降雨量更为敏感,所需的临界降雨量相对较小,预示这些地区更容易受洪水影响。
3 洪水预警技术
3.1 统计分析
表2为永昌县和夏河县地形特征要素和洪水计算要素的调查与插值结果统计分析。通过统计分析,发现调查结果中洪峰流量、主沟道长度和临界雨量的均方差较大,分别为154.01 m³·s-1、11.43 km和11.37 mm。表明研究区内数据的离散性较大,反映出地形和气候的多样性,有助于揭示该区域内洪水的特征。然而,在进行插值后,洪峰流量和主沟道长度的均方差分别减小为77.76 m³·s-1和1.48 km。这是因为插值过程增加了数据点的数量,同时对数据进行了填充,从而减小了均方差。值得注意的是,各调查点的气象数据是由附近气象监测站的数据插值而来,加之气候特征不易受地形条件影响,因此临界雨量的变化相对较小。
表2 地形特征要素和洪水计算要素的插值结果与实际调查结果的统计分析
Tab.2
| 统计参数 | 调查结果 | 插值结果 | 差值 | |||||
|---|---|---|---|---|---|---|---|---|
| 均值 | 中值 | 均方差 | 均值 | 中值 | 均方差 | 均值差百分比绝对值/% | 中值差百分比绝对值/% | |
| 主沟道长度/km | 12.89 | 6.59 | 11.43 | 7.98 | 7.75 | 1.48 | 38.09 | 17.56 |
| 主沟比降/‰ | 50.15 | 44.15 | 26.67 | 54.19 | 58.53 | 9.67 | 8.05 | 32.58 |
| 汇流时间/h | 3.42 | 2.69 | 1.88 | 2.52 | 2.70 | 0.49 | 26.42 | 0.42 |
| 100 a重现期降雨量/mm | 51.25 | 53.00 | 10.80 | 49.25 | 54.53 | 9.55 | 3.91 | 2.89 |
| 暴雨时程分配/mm | 7.24 | 7.00 | 0.76 | 7.24 | 6.92 | 0.55 | 0.00 | 1.20 |
| 设计洪峰流量/(m3·s-1) | 159.49 | 75.10 | 154.01 | 126.17 | 103.05 | 77.76 | 20.89 | 37.22 |
| 临界雨量/mm | 34.08 | 34.90 | 11.37 | 32.34 | 38.77 | 11.57 | 5.11 | 11.10 |
| 准备转移雨量/mm | 22.20 | 22.70 | 7.45 | 21.08 | 25.31 | 7.57 | 5.04 | 11.49 |
| 立即转移雨量/mm | 27.47 | 29.00 | 7.60 | 26.13 | 29.80 | 7.58 | 4.86 | 2.74 |
进一步分析均值差和中值差的百分比绝对值,发现主沟道长度和汇流时间的均值差百分比最大;而主沟比降和设计洪峰流量的中值差百分比则相对较大。主沟比降与主沟道长度的均值差异较大主要由于地形条件差异导致。设计洪峰流量插值后均值减小则是因为调查区内流域面积较小,设计洪峰流量偏小的小流域占据了较大的插值区域,从而导致插值后均值减小。
3.2 相关性分析
图6为夏河县和永昌县的洪水调查要素及雨量预警阈值的相关系数。可以看出,永昌县的小流域洪水因子与地形之间的相关性总体较好,除了暴雨时程分配外,相关系数均在0.59以上,均通过0.01的显著性检验。其中,设计洪峰流量与汇流时间、临界雨量和主沟道长度之间的相关性较强,相关系数均在0.90以上,均通过0.01的显著性检验。对于洪水预防,准备转移雨量与临界雨量、汇流时间、设计洪峰流量的相关系数分别为0.99、0.98、0.93,立即转移雨量与临界雨量、汇流时间、设计洪峰流量的相关系数分别为1.00、0.99、0.95,也均通过0.01的显著性检验。
图6
图6
夏河县和永昌县的洪水调查要素及雨量预警阈值的相关系数
Fig.6
Correlation analysis of flood investigation factors and warning threshold of rainfall for Xiahe County and Yongchang County
相比之下,夏河县的小流域洪水因子与地形之间的相关性相对较差,相关系数变化较大,但仍表现出一定的规律性,尤其是准备转移雨量和立即转移雨量与主沟比降之间的相关性较好,相关系数均为-0.65,且通过0.01的显著性检验。在洪水预防方面,准备转移雨量与临界雨量、暴雨时程分配、主沟比降的相关系数分别为1.00、0.44、-0.65,立即转移雨量与临界雨量、暴雨时程分配、主沟比降的相关系数分别为1.00、0.42、-0.65,也均通过0.01的显著性检验,相关性相对较好。
总体而言,对于洪水计算,设计洪峰流量与主沟比降之间的相关性较好;而在洪水预报方面,准备转移雨量与100 a重现期降雨量和临界雨量之间的相关性较强。尽管两个区域的洪水要素与雨量预警阈值存在一定的相关性,但整体上仍存在显著差异。如果排除降雨量的时空差异,地形差异主要源于主沟比降和坡度。
3.3 机器学习建模
通过对两个区域的洪水调查因子与预警参数之间的相关性分析,可以为建立小区域的经验预测模型提供依据,从而为未来的洪水评估提供科学支持。在经验模拟分析中,选择两个区域的准备转移雨量作为洪水预警参数,地形因素选取主沟比降,而降雨因子包括暴雨时程分配和临界雨量。
本文建模选择线性回归方法、随机森林算法及人工神经网络法(Kang et al., 2024)。永昌县和夏河县的洪水调查因素及预警指标分布图共有有效栅格数据20 835组,其中80%(16 668)的数据点用于训练模型,20%(4 167)的数据点用于验证模型。通过训练的经验模型得出的预警雨量与理论经验模型计算的预警雨量采用均方根误差(Root Mean Square Error,RMSE)、均方差(Mean Square Error,MSE)、决定系数(R2)、平均绝对误差(Mean Absolute Error,MAE)和平均绝对误差百分比(Mean Absolute Percentage Error, MAPE)进行分析评价。
3.3.1 多元线性回归方法
多元线性模型回归方法是基于假设多个输入变量与输出变量是线性组合,通过多个输入变量来生成输出变量。基于准确性的评价指标,通过不断调整,求解线性组合中的最优系数。
通过模型训练发现,准备转移雨量与其他要素的线性回归关系为:准备转移雨量=0.259×暴雨时程分配+0.663×临界雨量+0.006 9×主沟比降。对于训练组数据,MSE、RMSE和R2分别为0.003 67、0.061和0.99。而对于验证组数据,MSE、RMSE和R2分别为0.004 2、0.065和0.99。图7训练组和验证组理论经验模型计算结果与机器学习模型结果对比,说明机器学习模型结果与理论经验模型结果基本吻合。
图7
图7
训练组和验证组理论经验模型计算结果与机器学习模型结果的散点图
Fig.7
Scatter plots of the calculation results of the theoretical empirical model and the machine learning model of the training group and validation group
3.3.2 随机森林算法
采用随机森林算法对所有数据样本进行回归分析发现,原始采集数据点的回归结果R²为0.994 7,而插值后数据点的回归分析结果R²为0.992 1。表明随机森林算法能够提供相对可靠的回归模型,且原始调查数据与插值后数据的回归分析结果差异不大。然而,模型在小数据量上的适用性仍需进一步验证。
3.3.3 人工神经网络
人工神经网络(Artificial Neural Network,ANN)是一种适用于多变量之间相关性分析的回归分析方法。ANN的主要结构由输入层、隐藏层和输出层组成,每个节点都有相应的权重,这些权重通过激活函数计算得出。ANN的优势在于能够在大量输入变量的情况下最大化利用信息。
针对调查数据点和插值数据点,采用ANN方法进行分析(表3),分析中,隐藏层采用了两层和五层,而神经元数量分别为常用的5个和20个。结果显示,虽然R²可以总体评价回归分析的结果,但很难区分不同层数和神经元数对计算结果的影响。因此,采用其他4个评价指标(MAE、MSE、RMSE和MAPE)进一步对回归分析结果进行评价。
表3 基于人工神经网络计算的准备转移雨量各项评价指标
Tab.3
| 项目 | 层数 | 神经元数 | 批量 | 迭代列表 | MAE/mm | MSE/mm2 | RMSE/mm | MAPE/% | R2 |
|---|---|---|---|---|---|---|---|---|---|
| 调查数据点 | 2 | 5 | 5 | 100 | 0.532 | 0.430 | 0.656 | 0.034 | 0.994 |
| 2 | 20 | 10 | 100 | 0.248 | 0.101 | 0.318 | 0.016 | 0.999 | |
| 3 | 5 | 5 | 100 | 0.503 | 0.385 | 0.620 | 0.032 | 0.994 | |
| 3 | 20 | 10 | 100 | 0.209 | 0.070 | 0.264 | 0.013 | 0.999 | |
| 插值数据点 | 2 | 5 | 5 | 5 | 0.059 | 0.007 | 0.086 | 0.004 | 1.000 |
| 2 | 20 | 15 | 50 | 0.064 | 0.007 | 0.085 | 0.004 | 1.000 | |
| 3 | 5 | 5 | 50 | 0.074 | 0.009 | 0.093 | 0.093 | 1.000 | |
| 3 | 20 | 5 | 50 | 0.110 | 0.015 | 0.121 | 0.006 | 1.000 |
分析结果一致表明,对于调查数据点,神经元数量是影响回归分析结果的主要因素。而在插值数据点的回归分析中,由于数据点相对较多,层数和神经元数对结果的影响不大。采用不同层数和神经元数的情况下,两个隐藏层的回归分析结果较优,但与三个隐藏层之间的区别不显著。
3.4 模型应用
为验证模型的合理性,将新的回归模型应用于同样位于半干旱区的甘肃省合作市34个调查流域。由于线性回归模型与随机森林算法及神经网络法得到的结果差异较小,考虑模型推广的实际应用,仅对线性回归模型进行了进一步验证和评估。
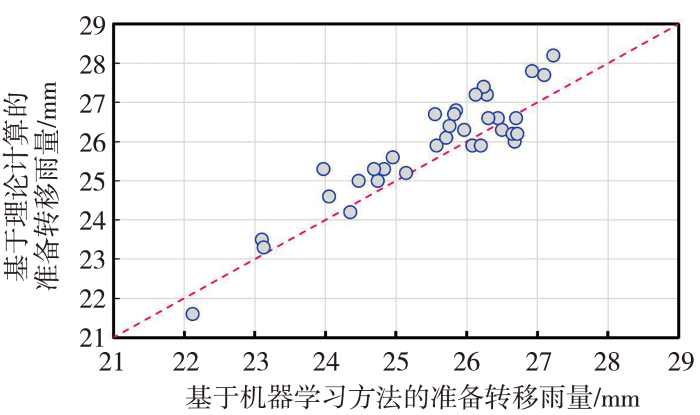
图8为合作市准备转移雨量的理论计算结果与机器学习结果比较。可以看出,两种模型计算的准备转移雨量非常接近,最大偏差仅为1.32 mm,平均绝对误差为0.56 mm。尽管气候、降雨等因素的时空差异可能对准备转移雨量的计算结果产生一定影响,但本文中机器模型为小流域洪水阈值计算提供了一种新的方法。
图8
图8
甘肃省合作市准备转移雨量的理论计算结果与机器学习结果比较
Fig.8
Comparison of theoretical calculation results and machine learning results of prepared transfer rainfall in Hezuo City of Gansu Province
4 结论与讨论
为解决干旱半干旱区中小流域洪水预报的难题,本文选取甘肃省夏河县(位于半干旱区)和永昌县(位于干旱区)作为研究对象,采用“铁一院”法、瞬时单位线法和地区经验公式法计算两个地区的汇流时间、设计暴雨和设计洪水,并推算了洪水预警值。此外,还运用机器学习方法建立了洪水预警模型,并对其适用性进行验证。
研究调查显示,永昌县和夏河县的准备转移雨量分别为11~19 mm和25~34 mm。调查结果表明,在相同降雨重现期内,雨量的变化范围与降雨频率有较强的相关性,降雨频率越小,雨量变化越大。
采用机器学习方法建立了线性回归、随机森林和神经网络3种经验模型。研究发现,线性回归模型、随机森林算法和神经网络法的结果差异较小。因此,在模型推广应用时,进一步验证和评估线性回归模型。结果表明,新模型计算的甘肃省合作市(位于半干旱区)准备转移雨量的平均绝对误差仅为0.56 mm。因此,该模型为干旱半干旱区的洪水阈值因子计算提供了新的参考方法。
新的经验回归模型是基于两个区域的数据进行模型训练,由于气候、降雨等因素的时空差异,计算结果还存在一定偏差。随着调查数据的丰富,经验模型也会不断完善,回归预测结果也会趋于稳定和更加准确。
参考文献
一种基于神经网络的中国区域夏季降水预测订正算法
[J].基于CWRF(climate extension of WRF)区域气候模式的动力降尺度预测技术对夏季降水预测存在一定偏差,难以实现准确预测。本文立足于中国区域夏季降水特点,分析与夏季降水相关的气象要素,采用树突(dendrite,DD)网络与人工神经网络(artificial neural networks,ANN)相结合的方法,针对CWRF模式回报的1996—2019年夏季降水量进行订正,检验其订正效果。结果表明:人工树突神经网络(artificial dendritic neural network,ADNN)算法模型订正的中国夏季降水量整体好于CWRF模式历史回报,距平相关系数和时间相关系数较订正前均提高约0.10,均方误差下降约26%,趋势异常综合检验评分提高6.55,表明ADNN机器学习方法能够对CWRF模式夏季降水预测实现一定程度的订正,从而提高该模式降水预测精度。
西北东部半干旱区一次极端特大暴雨的触发和维持机制
[J].2022年7月15日地处西北东部半干旱区的甘肃庆阳出现特大暴雨,多站日雨量和小时雨量均突破历史极值,利用多源观测资料和ERA5再分析资料,针对这次特大暴雨过程形成机制进行分析。结果表明,本次过程是发生在黄土高原复杂地形下弱天气尺度斜压强迫、弱不稳定能量及深厚湿层背景下的暖区暴雨,局地性强、强降水持续时间长;南亚高压、副热带高压及低层气压系统上下叠加的环流形势配置有利于中尺度对流系统发生发展;地面辐合线和偏南低空急流触发对流系统初生、发展,低空急流的发展和长时间维持使地面辐合线不断加强,同时急流左侧(暴雨区)与其出口区和入口区右侧形成的稳定次级环流是对流系统维持的关键,而凝结潜热释放引发的局地锋生、低层正涡度发展则是对流系统发展维持的另一重要因素,同时也是大气不稳定度维持的重要原因。中尺度对流系统呈现深厚低质心、准静止特征,雷达回波具有后向传播和列车效应特征。
甘肃陇南两次暴雨天气过程对比分析
[J].2017年8月甘肃陇南出现暴雨天气,礼县、武都气象站24 h降水量突破历史极值,极端性和局地性突出。应用欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)第5代全球大气再分析产品ERA5、雷达资料及地面加密观测资料,对2017年8月6—7日、19—20日发生在甘肃省陇南地区的2次暴雨过程进行对比分析,重点讨论2次过程的环流背景以及强降水时段雷达反射率因子、径向速度、物理量特征。结果表明,2次暴雨过程均发生在西风槽偏北气流与中低层偏南暖湿气流交汇处,但是2次过程的主要影响系统及触发条件不同;雷达回波显示8月6—7日由冷式切变线引起的暴雨系统对流性较强,反射率因子值较高、中心高度较低,降水率较大,持续时间短;19—20日暖区降水的反射率因子值较低、中心高度较高,降水率较小,持续时间较长。
基于人工神经网络算法的渤海海风预报方法研究
[J].基于2015—2017年常规海洋气象观测资料、天津中尺度天气预报模式(TJ-WRF)预报产品、EC数值预报及其集合预报产品,建立了渤海BP神经网络两级海风预报模型,该模型在大量历史样本的拟合训练基础上分别实现小风和大风与相关因子间的非线性映射,其结果有较高的预报准确率。一年的业务试用期间,该模型对各风级、各预报时效的预报能力基本稳定,预报误差较使用该释用技术前数值模式误差有所减小,72 h内风速平均绝对误差为1.72 m·s-1;对灾害大风的预报准确率仍能保持较高水平,8级风风速平均绝对误差仅为1.77 m·s-1。
深度学习模型在2021年汛期武汉市雷达回波临近预报中的应用评估
[J].近年来,人工智能技术在图像识别领域取得了突破性进展,为探寻人工智能模型在武汉地区雷达回波临近预报中的应用价值,本文利用湖北武汉市2015—2020年雷达回波和降水量观测资料,对PredRNN++、MIM、CrevNet和PhyDNet 4种深度学习模型进行雷达回波临近预报训练,并基于2021年汛期雷达回波资料进行雷达回波临近预报。在此基础上,通过降水强度和降水面积指数筛选降水过程,并以均方误差(Mean Square Error, MSE)、结构相似性指数(Structural Similarity Index Measurement, SSIM)、命中率(Probability of Detection, POD)、空报率(False Alarm Rate, FAR)和临界成功指数(Critical Success Index, CSI)为指标,检验评估上述4种深度学习模型和光流法对2021年汛期武汉地区雷达回波的临近预报性能。结果表明:(1)整体来看,MIM模型的MSE最小、POD最高,MIM和PredRNN++模型的SSIM并列最高;所有深度学习模型的FAR均低于光流法,且PhyDNet模型的FAR最低;除CrevNet模型外,其余3种深度学习模型的CSI均高于光流法,且MIM模型的CSI最高。(2)预报的前12 min,光流法的CSI最高,而在18~120 min MIM模型的CSI最高,显示了深度学习模型长预报时效的优势。(3)随着回波强度增加,深度学习模型和光流法的POD和CSI均迅速降低,而FAR光流法与各模型则表现出不同的变化规律。(4)随着区域性降水强度增加,深度学习模型的预报能力均先降低后明显增强,而光流法对降水强度变化的敏感性较弱,故在强降水背景下深度学习模型的CSI较光流法增幅最大;对于局地一般对流性降水过程,所有深度学习模型和光流法的预报能力均大幅降低。(5)暴雨个例分析结果表明,深度学习模型不仅具备一定回波强度变化的预报能力,而且对回波运动的预报能力也明显高于光流法,展示了深度学习模型良好的应用前景。
Simulated investigation on the impact of spatial-temporal variability of rainstorms on flash flood discharge process in small watershed
[J].
A comprehensive flash flood defense system in China: Overview, achievements, and outlook
[J].
Flood-runoff in semi-arid and sub-humid regions, a case study: A simulation of Jianghe watershed in Northern China
[J].
Examination of the correlation between SPT and undrained shear strength: Case study of clay till in Alberta, Canada
[J].
Compressive strength of fly-ash-based geopolymer concrete by gene expression programming and random forest
[J].
Landslide hazards zonation using GIS in Khoramabad, Iran
[J].
Thirteen ways to look at the correlation coefficient
[J].
Kriging: A method of interpolation for geographical information systems
[J].
A novel hybrid soft computing model using random forest and particle swarm optimization for estimation of undrained shear strength of soil
[J].
Identification of the key driving factors of flash flood based on different feature selection techniques coupled with random forest method
[J].
Assessing the applicability of conceptual hydrological models for design flood estimation in small-scale watersheds of Northern China
[J].